| An electric current produces a magnetic field. This applet simulates an experiment concerning the magnetic field of a straight current-carrying wire. A large current passes through a vertical wire. You can reverse the direction of this current by using the red button. The signs at the ends of the wire symbolize the poles of the connected battery. The conventional direction of current is given by the red arrow. Note that the motion of the electrons (green dots) is opposite to the conventional direction! A compass needle which can be moved (by dragging the mouse with pressed mouse button) shows the direction of the magnetic field (blue) at a given position. North and south pole of the compass needle are painted with red respectively green colour. The influence of the earth's magnetic field is neglected in this simulation. The magnetic field lines of a straight current-carrying wire form concentric circles around the wire. The direction of the magnetic field (blue arrows) is given by the right-hand rule: When the thumb of the right hand points in the direction of the conventional current, the fingers curl around the wire in the direction of the magnetic field. URL: http://home.a-city.de/walter.fendt/phe/mfwire.htm © Walter Fendt, September 18, 2000 - Magnetic Field Due To Current In A Straight Wire
- Properties Of Magnets
- Induced Magnetism & Electrical Method Of Magnetisation
- Magnetic Field & Magnetic Field Lines
- Temporary & Permanent Magnets
- Magnetic Field Due To Current In A Solenoid
- Electric Bell
- Circuit Breaker
- Force On A Current-carrying Conductor & Fleming's Left Hand Rule
- Electromagnetic Induction & Lenz's Law
- A.C. Generator
- Workings Of A Transformer
- Practice MCQs For Simple Phenomena Of Magnetism, Force on Conductor in a Magnetic Field, Electromagnetic Force
- O Level Physics Topic List
Table of ContentsThe exploration of electromagnetism reveals that the movement of electric charges is a fundamental cause of magnetism. This principle is crucial for understanding how electric currents, which constitute flows of charge, generate magnetic fields. The nature of these magnetic fields is inherently linked to the configuration of the conductor through which the current flows. When an electric current traverses a straight wire, it induces a magnetic field whose lines of force are concentric circles centered around the wire. This configuration illustrates the intimate relationship between electricity and magnetism, highlighting how electrical currents can create magnetic environments. The Right-Hand Rule: Determining the Direction of Magnetic Fields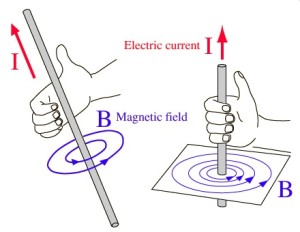 A pivotal tool in the study of electromagnetism is the Right-Hand Rule, which provides a straightforward method for identifying the direction of the magnetic field surrounding a current-carrying conductor. This rule states: - Positioning the Hand : Extend your right hand, and grasp the wire such that your thumb points in the direction of the conventional current (from positive to negative).
- Determining the Field Direction : With your hand in this position, your fingers naturally curl around the wire. The direction in which your fingers wrap around the wire corresponds to the direction of the magnetic field lines generated by the current.
Characteristics of the Magnetic FieldThe strength of the magnetic field generated by a current is not uniform; it varies with distance from the wire: - Near the Wire : The magnetic field is most intense close to the carrying conductor. Here, the field lines are densely packed, indicating a stronger magnetic effect.
- Away from the Wire : As one moves further from the wire, the magnetic field’s intensity diminishes. This decrease in strength is visually represented by the spacing between the concentric circles of the magnetic field, which become farther apart with increased distance from the wire.
Furthermore, the magnitude of the electric current influences the magnetic field’s strength. A larger current will produce a more robust magnetic field, accentuating the dynamic relationship between electrical and magnetic phenomena. This relationship underscores the foundational principles of electromagnetism, providing a framework for understanding the complex interactions between electric currents and the magnetic fields they induce. 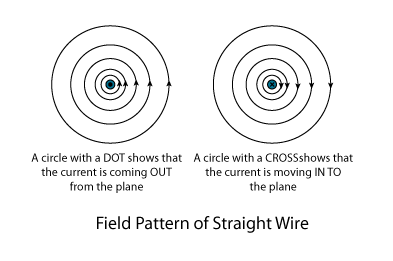  Worked ExamplesExample 1: calculating magnetic field orientation. A student sets up an experiment with a straight wire carrying a current of 5 A. The current flows from the west to the east. Using the Right-Hand Rule, determine the direction of the magnetic field on the north side of the wire. To apply the Right-Hand Rule, extend your right hand so that your thumb points in the direction of the conventional current, which is from west to east in this case. When you wrap your fingers around the wire, they curl in the direction of the magnetic field. On the north side of the wire, your fingers will point towards you, indicating that the magnetic field is directed out of the page or screen. Therefore, the magnetic field on the north side of the wire is directed outwards, towards the observer. Example 2: Understanding Magnetic Field StrengthImagine two wires, Wire A and Wire B, running parallel to each other. Wire A carries a current of 10 A, and Wire B carries a current of 2 A. Both currents flow in the same direction. Without calculating specific values, compare the magnetic field strength generated by each wire at a point 5 cm away from each wire and explain the reasoning. The strength of the magnetic field generated by a current-carrying wire decreases with distance from the wire but is also directly proportional to the magnitude of the current flowing through the wire. Therefore, at the same distance $5 \text{ cm}$ from each wire, Wire A, which carries a larger current $10 \text{ A}$, produces a stronger magnetic field than Wire B, which carries a smaller current $2 \text{ A}$. This illustrates the principle that a larger current results in a more robust magnetic field at any given point away from the wire, provided the distance is the same. Example 3: Magnetic Field Lines in a CoilA coil consists of 5 turns of wire, with an electric current of 3 A flowing through it. The coil is laid flat on a table, and the current flows in a clockwise direction when viewed from above. Using the Right-Hand Rule, determine the direction of the magnetic field through the center of the coil. To apply the Right-Hand Rule to a coil, you can follow the direction of the current in the turns of the wire. For a coil with the current flowing in a clockwise direction when viewed from above, place your right hand above the coil with your fingers following the direction of the current (clockwise). Since your fingers curl in the direction of the current flow, your thumb, when pointed straight down towards the center of the coil, indicates the direction of the magnetic field through the coil. Therefore, the magnetic field through the center of the coil is directed downwards, perpendicular to the plane of the coil lying on the table. Back To Magnetism & Electromagnetism (O Level Physics) Back To O Level Physics Topic List  Mini PhysicsAs the Administrator of Mini Physics, I possess a BSc. (Hons) in Physics. I am committed to ensuring the accuracy and quality of the content on this site. If you encounter any inaccuracies or have suggestions for enhancements, I encourage you to contact us . Your support and feedback are invaluable to us. If you appreciate the resources available on this site, kindly consider recommending Mini Physics to your friends. Together, we can foster a community passionate about Physics and continuous learning. Leave a Comment Cancel replyThis site uses Akismet to reduce spam. Learn how your comment data is processed . Lesson Explainer: The Magnetic Field due to a Current in a Straight Wire Physics • Third Year of Secondary SchoolJoin nagwa classes. Attend live Physics sessions on Nagwa Classes to learn more about this topic from an expert teacher!  In this explainer, we will learn how to calculate the magnetic field produced by a current in a straight wire. We know that a moving charge, or current, produces a magnetic field. A long, straight section of wire carrying a current 𝐼 is shown in the diagram below. Because there is current present in the wire, a magnetic field is produced around the wire and is composed of closed concentric circles, as represented by the gray loops in the diagram. The strength of the resulting magnetic field, 𝐵 , can be found at any distance 𝑑 away from the wire using the equation below. The Strength of the Magnetic Field due to a Current in a Straight WireThe strength of a magnetic field, 𝐵 , some distance 𝑑 away from a straight wire carrying a current, 𝐼 , can be found using the equation 𝐵 = 𝜇 𝐼 2 𝜋 𝑑 , where 𝜇 is a constant known as “the permeability of free space” and has the value 𝜇 = 4 𝜋 × 1 0 ⋅ / T m A . It should be noted that the distance 𝑑 must be measured perpendicular to the wire. A perpendicular distance measurement is shown in the diagram below. The strength of the field, 𝐵 , decreases as the distance away from the wire, 𝑑 , increases. This is illustrated in the diagram below, which shows a view along the length of a straight current-carrying wire. It should be noted that the dot in the center of the wire indicates that the current points out of—and perpendicular to—the screen. Areas where the field lines are closer together indicate where the field is stronger. Although only some field lines are shown above, the field is technically present even infinitely far away from the wire. However, the strength of the field is negligibly small very far away. This is because the distance 𝑑 appears in the denominator of the equation for magnetic field strength; thus, 𝐵 and 𝑑 are inversely proportional to each other and the magnetic field strength goes to 0 as 𝑑 goes to infinity. This proportionality is shown in the graph below. Let us practice using the equation for the magnetic field due to a straight current-carrying wire. Example 1: Calculating the Magnetic Field due to a Current in a Straight WireA long, straight cable in an industrial power plant carries a direct current of 100 A . Calculate the strength of the resulting magnetic field at a perpendicular distance of 0.06 m from this cable. Use 4 𝜋 × 1 0 T⋅m/A for the value of 𝜇 . Give your answer in scientific notation to two decimal places. To begin, let us recall the equation to determine the magnetic field strength a distance 𝑑 away from a straight wire carrying a current 𝐼 , 𝐵 = 𝜇 𝐼 2 𝜋 𝑑 . Since we have been given values for 𝜇 , 𝐼 , and 𝑑 , we are ready to substitute them in and solve for the strength of the magnetic field, 𝐵 . Thus, we have 𝐵 = 4 𝜋 × 1 0 ⋅ / ( ) 2 𝜋 ( 0 . 0 6 ) . T m A A m We can simplify the math by canceling some terms and units. We will cancel the units of metres because m appears in the numerator and the denominator. The numerator includes both 1 /A and A , so amperes will also cancel out. This leaves us with only the unit of magnetic field strength, teslas . Further, we can cancel 2 𝜋 from the numerator and denominator, so we have 𝐵 = 2 × 1 0 ( 1 0 0 ) 0 . 0 6 = 3 . 3 3 3 × 1 0 . T T Rounding to two decimal places, the answer is 3 . 3 3 × 1 0 T . Beyond using precise values to calculate the strength of a field, we can use the magnetic field equation to explore some more conceptual properties. Example 2: Determining a Proportionality for the Magnetic Field due to a Current in a Straight WireA long, straight wire is carrying a direct current, which produces a magnetic field of strength 𝐵 teslas at a perpendicular distance of 𝑑 cm from the wire. Assuming the system does not change, what is the relationship between 𝐵 and the strength of the magnetic field strength 𝐵 at a perpendicular distance of 2 𝑑 cm from the wire? Assume 𝐵 and 𝐵 are much greater than the magnetic field strength of Earth. - 𝐵 = 1 4 𝐵
- 𝐵 = 1 2 𝐵
- 𝐵 = 2 𝐵
- 𝐵 = 4 𝐵
Let us begin by recalling the equation to determine the magnetic field strength some distance away from a straight current-carrying wire, 𝐵 = 𝜇 𝐼 2 𝜋 𝑑 . Here, we have two measurements of field strength, 𝐵 and 𝐵 , measured at distances that we will call 𝑑 and 𝑑 respectively. We are told that all other properties of the system are constant, and therefore, the quantity 𝜇 𝐼 2 𝜋 is equivalent in both cases. We can devise a ratio to relate these values: 𝐵 𝐵 = 𝑑 𝑑 . Comparing the measured distances from the wire, we know that 𝑑 is twice as great as 𝑑 , so 𝑑 = 2 𝑑 . Substituting this into the equation above, we have 𝐵 𝐵 = 2 𝑑 𝑑 . Now, we can cancel the 𝑑 terms on the right side of the equation: 𝐵 𝐵 = 2 . Now, solving for 𝐵 , 𝐵 = 1 2 𝐵 . Thus, the magnetic field strength 𝐵 is measured at twice the distance from the wire as 𝐵 and has half the strength of 𝐵 . Therefore, choice B is correct. Example 3: Calculating the Current in a Straight Wire given the Magnetic Field StrengthA straight wire in an electrical circuit carries a direct current of 𝐼 A . The resulting magnetic field at a perpendicular distance of 18 mm from this wire is measured to be 1 . 2 × 1 0 T . Calculate 𝐼 to the nearest ampere . Use 4 𝜋 × 1 0 T⋅m/A for the value of 𝜇 . Here, we are given a value for the magnetic field produced by a current in a straight wire, and we have been told to find the value of the current. We can begin by recalling the equation for the magnetic field strength due to a straight current-carrying wire, 𝐵 = 𝜇 𝐼 2 𝜋 𝑑 . To solve for the current, 𝐼 , we will multiply both sides of the equation by 2 𝜋 𝑑 𝜇 . Thus, we have 𝐼 = 2 𝜋 𝑑 𝐵 𝜇 . Before we continue, we will convert our distance value into metres , since it is given to us in millimetres . We know that 𝑑 = 1 8 = 0 . 0 1 8 m m m . Now, substituting all of our values in, we have 𝐼 = 2 𝜋 ( 0 . 0 1 8 ) 1 . 2 × 1 0 4 𝜋 × 1 0 ⋅ / = 1 0 . 8 . m T T m A A Rounding to the nearest ampere , we have found that the current in the wire is 11 A . Thus far, we have only been concerned with the magnitude, or strength, of a magnetic field due to current in a wire. However, we must remember that magnetic field is a vector quantity, since it is defined using both a magnitude and a direction. We will use the right-hand rule to determine the direction of the magnetic field, as described below. Rule: Right-Hand Rule for the Magnetic Field due to a Current in a Straight WireTo determine the direction of the magnetic field due to a straight current-carrying wire, perform the following steps: - Using the right hand, point the thumb in the direction of the current.
- “Grab“ the wire, curling the fingers around its imaginary axis. The direction that the fingers curl in corresponds to the direction of the magnetic field.
The diagram below shows how to use the right hand to wrap around the axis of the wire. Notice how the thumb points along the direction of the current and that the fingers curl in the same direction as the magnetic field. We will practice using the right-hand rule in the next example. Example 4: Using the Right-Hand Rule for the Magnetic Field due to a Current in a Straight WireA long, straight wire is carrying a constant current 𝐼 that induces a magnetic field 𝐵 . Magnetic field lines of 𝐵 are shown in the diagram. Based on the diagram, state the direction of the conventional current in the wire. Recall that moving charges produce a magnetic field and that we can determine the direction of the current in the wire using the right-hand rule. To do so, use the right hand to “grab” the wire, with the thumb pointing in the direction of the current. Then, curl the fingers into a fist, and the direction that the fingers curl in indicates the direction of the resulting magnetic field. To test whether the current is going from bottom to top, we point the thumb upward and curl the fingers. In this case, as viewed from above (like in the diagram), the magnetic field would be pointing counterclockwise. This is contrary to what is shown in the diagram, so we know that the current is not moving from bottom to top. We can make sure that the current is indeed moving from top to bottom by making a thumbs-down shape with the right hand. Like in the diagram, as viewed from above, the fingers (and therefore the magnetic field) curl clockwise. Therefore, the current in the wire is moving from top to bottom. Thus, we have seen how to determine the magnitude and direction of the magnetic field due to a current in a straight wire. Let us finish by summarizing a few important concepts. - A long, straight, current-carrying wire produces a magnetic field composed of concentric closed circles, and the field strength is given by 𝐵 = 𝜇 𝐼 2 𝜋 𝑑 .
- The strength of the magnetic field, 𝐵 , is inversely proportional to the distance away from the wire, 𝑑 . Thus, the field strength falls off to zero as 𝑑 gets very large.
- We can determine the direction of the magnetic field using the right-hand rule: point the thumb in the direction of the current and curl the fingers as if grabbing the wire. The direction that the fingers curl in corresponds to the direction of the magnetic field.
Attend live sessions on Nagwa Classes to boost your learning with guidance and advice from an expert teacher! - Interactive Sessions
- Chat & Messaging
- Realistic Exam Questions
 Nagwa uses cookies to ensure you get the best experience on our website. Learn more about our Privacy Policy 22.9 Magnetic Fields Produced by Currents: Ampere’s LawLearning objectives. By the end of this section, you will be able to: - Calculate current that produces a magnetic field.
- Use the right hand rule 2 to determine the direction of current or the direction of magnetic field loops.
How much current is needed to produce a significant magnetic field, perhaps as strong as the Earth’s field? Surveyors will tell you that overhead electric power lines create magnetic fields that interfere with their compass readings. Indeed, when Oersted discovered in 1820 that a current in a wire affected a compass needle, he was not dealing with extremely large currents. How does the shape of wires carrying current affect the shape of the magnetic field created? We noted earlier that a current loop created a magnetic field similar to that of a bar magnet, but what about a straight wire or a toroid (doughnut)? How is the direction of a current-created field related to the direction of the current? Answers to these questions are explored in this section, together with a brief discussion of the law governing the fields created by currents. Magnetic Field Created by a Long Straight Current-Carrying Wire: Right Hand Rule 2Magnetic fields have both direction and magnitude. As noted before, one way to explore the direction of a magnetic field is with compasses, as shown for a long straight current-carrying wire in Figure 22.37 . Hall probes can determine the magnitude of the field. The field around a long straight wire is found to be in circular loops. The right hand rule 2 (RHR-2) emerges from this exploration and is valid for any current segment— point the thumb in the direction of the current, and the fingers curl in the direction of the magnetic field loops created by it. The magnetic field strength (magnitude) produced by a long straight current-carrying wire is found by experiment to be where I I is the current, r r is the shortest distance to the wire, and the constant μ 0 = 4π × 10 − 7 T ⋅ m/A μ 0 = 4π × 10 − 7 T ⋅ m/A is the permeability of free space . ( μ 0 ( μ 0 is one of the basic constants in nature. We will see later that μ 0 μ 0 is related to the speed of light.) Since the wire is very long, the magnitude of the field depends only on distance from the wire r r , not on position along the wire. Example 22.6Calculating current that produces a magnetic field. Find the current in a long straight wire that would produce a magnetic field twice the strength of the Earth’s at a distance of 5.0 cm from the wire. The Earth’s field is about 5 . 0 × 10 − 5 T 5 . 0 × 10 − 5 T , and so here B B due to the wire is taken to be 1 . 0 × 10 − 4 T 1 . 0 × 10 − 4 T . The equation B = μ 0 I 2 πr B = μ 0 I 2 πr can be used to find I I , since all other quantities are known. Solving for I I and entering known values gives So a moderately large current produces a significant magnetic field at a distance of 5.0 cm from a long straight wire. Note that the answer is stated to only two digits, since the Earth’s field is specified to only two digits in this example. Ampere’s Law and OthersThe magnetic field of a long straight wire has more implications than you might at first suspect. Each segment of current produces a magnetic field like that of a long straight wire, and the total field of any shape current is the vector sum of the fields due to each segment. The formal statement of the direction and magnitude of the field due to each segment is called the Biot-Savart law . Integral calculus is needed to sum the field for an arbitrary shape current. This results in a more complete law, called Ampere’s law , which relates magnetic field and current in a general way. Ampere’s law in turn is a part of Maxwell’s equations , which give a complete theory of all electromagnetic phenomena. Considerations of how Maxwell’s equations appear to different observers led to the modern theory of relativity, and the realization that electric and magnetic fields are different manifestations of the same thing. Most of this is beyond the scope of this text in both mathematical level, requiring calculus, and in the amount of space that can be devoted to it. But for the interested student, and particularly for those who continue in physics, engineering, or similar pursuits, delving into these matters further will reveal descriptions of nature that are elegant as well as profound. In this text, we shall keep the general features in mind, such as RHR-2 and the rules for magnetic field lines listed in Magnetic Fields and Magnetic Field Lines , while concentrating on the fields created in certain important situations. Making Connections: RelativityHearing all we do about Einstein, we sometimes get the impression that he invented relativity out of nothing. On the contrary, one of Einstein’s motivations was to solve difficulties in knowing how different observers see magnetic and electric fields. Magnetic Field Produced by a Current-Carrying Circular LoopThe magnetic field near a current-carrying loop of wire is shown in Figure 22.38 . Both the direction and the magnitude of the magnetic field produced by a current-carrying loop are complex. RHR-2 can be used to give the direction of the field near the loop, but mapping with compasses and the rules about field lines given in Magnetic Fields and Magnetic Field Lines are needed for more detail. There is a simple formula for the magnetic field strength at the center of a circular loop . It is where R R is the radius of the loop. This equation is very similar to that for a straight wire, but it is valid only at the center of a circular loop of wire. The similarity of the equations does indicate that similar field strength can be obtained at the center of a loop. One way to get a larger field is to have N N loops; then, the field is B = Nμ 0 I / ( 2 R ) B = Nμ 0 I / ( 2 R ) . Note that the larger the loop, the smaller the field at its center, because the current is farther away. Magnetic Field Produced by a Current-Carrying SolenoidA solenoid is a long coil of wire (with many turns or loops, as opposed to a flat loop). Because of its shape, the field inside a solenoid can be very uniform, and also very strong. The field just outside the coils is nearly zero. Figure 22.39 shows how the field looks and how its direction is given by RHR-2. The magnetic field inside of a current-carrying solenoid is very uniform in direction and magnitude. Only near the ends does it begin to weaken and change direction. The field outside has similar complexities to flat loops and bar magnets, but the magnetic field strength inside a solenoid is simply where n n is the number of loops per unit length of the solenoid ( n = N / l ( n = N / l , with N N being the number of loops and l l the length). Note that B B is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform fields spread over a large volume are possible with solenoids, as Example 22.7 implies. Example 22.7Calculating field strength inside a solenoid. What is the field inside a 2.00-m-long solenoid that has 2000 loops and carries a 1600-A current? To find the field strength inside a solenoid, we use B = μ 0 nI B = μ 0 nI . First, we note the number of loops per unit length is Substituting known values gives This is a large field strength that could be established over a large-diameter solenoid, such as in medical uses of magnetic resonance imaging (MRI). The very large current is an indication that the fields of this strength are not easily achieved, however. Such a large current through 1000 loops squeezed into a meter’s length would produce significant heating. Higher currents can be achieved by using superconducting wires, although this is expensive. There is an upper limit to the current, since the superconducting state is disrupted by very large magnetic fields. There are interesting variations of the flat coil and solenoid. For example, the toroidal coil used to confine the reactive particles in tokamaks is much like a solenoid bent into a circle. The field inside a toroid is very strong but circular. Charged particles travel in circles, following the field lines, and collide with one another, perhaps inducing fusion. But the charged particles do not cross field lines and escape the toroid. A whole range of coil shapes are used to produce all sorts of magnetic field shapes. Adding ferromagnetic materials produces greater field strengths and can have a significant effect on the shape of the field. Ferromagnetic materials tend to trap magnetic fields (the field lines bend into the ferromagnetic material, leaving weaker fields outside it) and are used as shields for devices that are adversely affected by magnetic fields, including the Earth’s magnetic field. PhET ExplorationsGenerate electricity with a bar magnet! Discover the physics behind the phenomena by exploring magnets and how you can use them to make a bulb light. Click to view content . This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission. Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax. Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units - Authors: Paul Peter Urone, Roger Hinrichs
- Publisher/website: OpenStax
- Book title: College Physics 2e
- Publication date: Jul 13, 2022
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
- Section URL: https://openstax.org/books/college-physics-2e/pages/22-9-magnetic-fields-produced-by-currents-amperes-law
© Jul 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.  | 

















IMAGES
VIDEO
COMMENTS
When the thumb of the right hand is aligned in the direction of current flow, the magnetic field produced by current in an infinite straight wire points in the direction of the curled fingers of the right hand.
Explain how the Biot-Savart law is used to determine the magnetic field due to a thin, straight wire. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire.
The magnetic field created by current following any path is the sum (or integral) of the fields due to segments along the path (magnitude and direction as for a straight wire), resulting in a general relationship between current and field known as Ampere’s law.
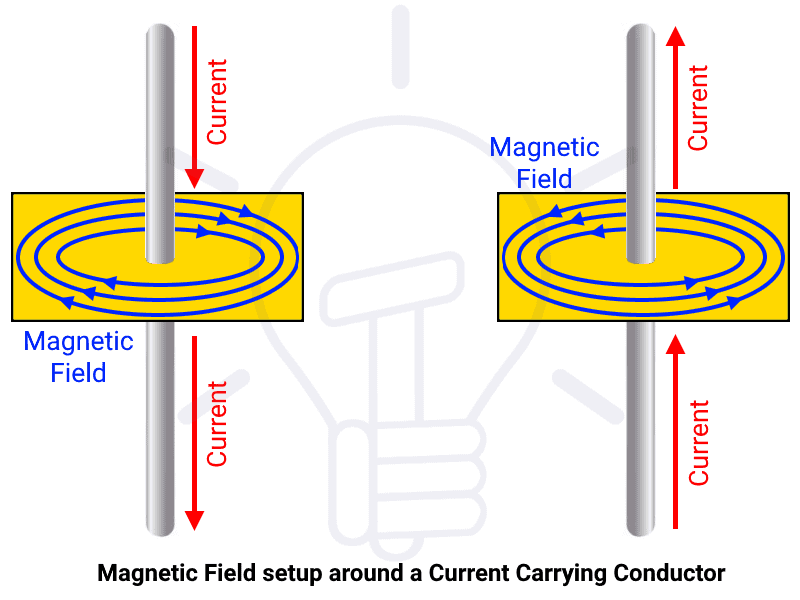
After many experiments, Oersted found that a straight current carrying conductor induces a magnetic field where the direction of magnetic field depends on the direction of flowing current in the conductor.
An electric current produces a magnetic field. This applet simulates an experiment concerning the magnetic field of a straight current-carrying wire. A large current passes through a vertical wire. You can reverse the direction of this current by using the red button.
When an electric current traverses a straight wire, it induces a magnetic field whose lines of force are concentric circles centered around the wire. This configuration illustrates the intimate relationship between electricity and magnetism, highlighting how electrical currents can create magnetic environments.
A long, straight, current-carrying wire produces a magnetic field composed of concentric closed circles, and the field strength is given by 𝐵 = 𝜇 𝐼 2 𝜋 𝑑 . The strength of the magnetic field, 𝐵 , is inversely proportional to the distance away from the wire, 𝑑 .
The magnetic force on a current-carrying wire in a magnetic field is given by \(\vec{F} = I\vec{l} \times \vec{B}\). For part a, since the current and magnetic field are perpendicular in this problem, we can simplify the formula to give us the magnitude and find the direction through the RHR-1.
Each segment of current produces a magnetic field like that of a long straight wire, and the total field of any shape current is the vector sum of the fields due to each segment. The formal statement of the direction and magnitude of the field due to each segment is called the Biot-Savart law.
a current-carrying wire produces a magnetic field around itself; the field reverses when the current is reversed; the field is stronger with more turns of the wire; A simple rule to use to show the direction of the current in a wire and the direction of its associated field is the right hand grip rule. With the thumb of a clenched right hand ...