Mass and weight – problems and solutions
Solved problems in Newton’s laws of motion – Mass, and weight
Wanted: weight (w)
The horizontal component of the weight :

Share this:
Leave a comment cancel reply.

StickMan Physics
Animated Physics Lessons
Mass and Weight
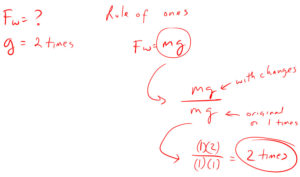
Learn the difference between mass (m) and weight (F w ). Find out how to convert to mass from weight and from weight to mass.
Watch the video as we go through the content and problems set or go through the same material below
Learning Targets
- I know the difference between mass and weight
- I can calculate mass from weight and weight from mass using F w = mg
- I can draw a Force Diagram of an object on a horizontal surface of any planet
Mass is a measurement of matter (molecular composition) of an object. Since an objects molecular composition remains when location changes, mass never changes.
Weight is a measure of the force of gravity on an objects mass. This is directly related to mass but will change with location as the force and acceleration due to gravity changes.
Weight equals mass times gravity
| Weight | F | Newton | N |
| Mass | m | kilogram | kg |
| Acceleration due to gravity | g | Meters per second squared | m/s |
- On the Earth's surface, the accepted value for acceleration due to gravity (g) is 9.81 m/s 2
- In some lessons we had you use a less specific rounded number of 10 m/s 2
Weight Changes When (g) Changes
On Earth, your weight is caused by the earths pull on you. In a future lesson we will see that weight is the result of the your mass, the earths mass, and the distance between you and Earth.
We will solve problems on this page using an average surface acceleration due to gravity
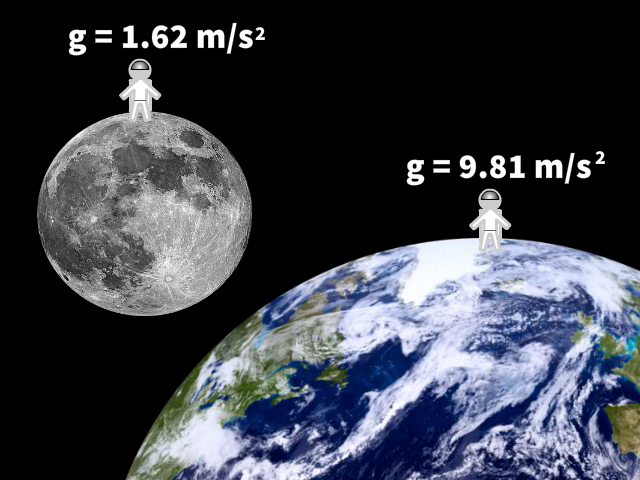
- More massive interstellar objects have a higher surface acceleration due to gravity ( g ).
- The higher the acceleration due to gravity ( g ) the higher the weight ( F w )
Mass, Radius, and Acceleration due to Gravity of Planets
| ) | |||
| Mercury | 3.29 x 10 | 2.440 x 10 | 3.70 |
| Venus | 4.87 x 10 | 6.052 x 10 | 8.88 |
| Earth | 5.97 x 10 | 6.378 x 10 | 9.81 |
| Mars | 6.39 x 10 | 3.396 x 10 | 3.72 |
| Jupiter | 1.90 x 10 | 7.149 x 10 | 24.79 |
| Saturn | 5.68 x 10 | 6.027 x 10 | 10.44 |
| Uranus | 8.68 x 10 | 2.556 x 10 | 8.69 |
| Neptune | 1.02 x 10 | 2.476 x 10 | 11.15 |

Mass, Radius, and Acceleration due to Gravity of Other Interstellar Objects
| ) | |||
| Sun | 1.99 x 10 | 6.963 x 10 | 274.78 |
| Earth’s Moon | 7.35 x 10 | 1.738 x 10 | 1.62 |
| Pluto | 1.31 x 10 | 1.195 x 10 | 0.62 |
Example Questions (Mass and Weight)
1. What is 76 kg Natalia's weight on earth where the acceleration due to gravity is 9.81 m/s 2 ?
See Solution
F w = (76)(9.81)= 745.56 N
2. What is Natalia's weight on the moon where the acceleration due to gravity is 1.62 m/s 2 ?
F w = (76)(1.62)= 123.12 N
3. If 76 kg Natalia went to Neptune where the surface acceleration due to gravity is 11.15 m/s 2 , would her mass or weight change and what would each be?
Mass would still be 76 kg wither location and weight would change
F w = (76)(11.15) = 847.4 N
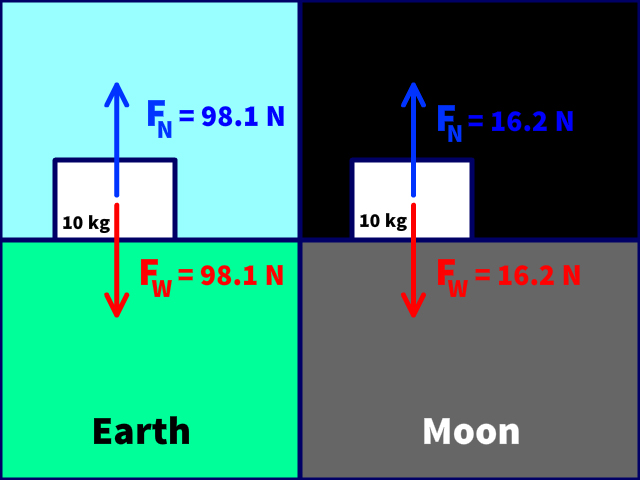
Normal Force Equals Weight on a Horizontal Surface
Notice in the force diagrams :
- Mass ( m ) of 10 kg does not change
- Weight ( F w ) changes with the acceleration due to gravity
- The normal ( F N )force changes with weight ( F w )
Normal force is the force created by weight on a surface pushing back upwards perpendicular to the surface. Perpendicular to any horizontal surface will be up.
Problem Set
1. What is the weight of a 25 kg object on Pluto where the acceleration due to gravity is 0.62 m/s 2 ?
F w = 15.5 N
2. Draw a force diagram including the normal force of this 25 kg object on a horizontal surface of Pluto where the acceleration due to gravity is 0.62 m/s 2 ?
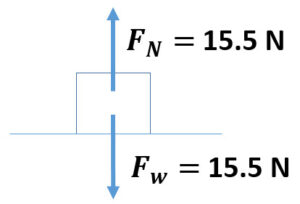
3. What is the mass of a 25 kg object on Pluto where the acceleration due to gravity is 0.62 m/s 2 ?
m = 25 kg (does not change)
4. What is the weight of a 25 kg object on Mars where the acceleration due to gravity is 3.72 m/s 2 ?
5. What is the mass of a 100 N object on the Moon where the acceleration due to gravity is 1.62 m/s 2 ?
6. Draw a force diagram including the normal force of a 100 N object on the surface of the Moon where the acceleration due to gravity is 1.62 m/s 2 ?
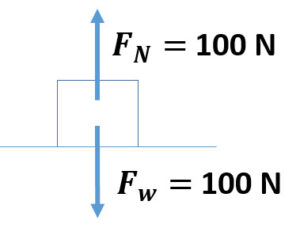
7. If you weigh 1177.2 N on Earth where the acceleration due to gravity is 9.81 m/s 2 what is your mass on Uranus where the acceleration due to gravity is 8.69 m/s 2 ?
8. If you weigh 1177.2 N on Earth where the acceleration due to gravity is 9.81 m/s 2 what is your weight on Uranus where the acceleration due to gravity is 8.69 m/s 2 ?
F w = 1042.8 N
Mass and Weight Quiz
Joe has a mass of 54 kg. What is his mass on the moon where the acceleration due to gravity is 1.62 m/s 2 ?
Mass does not change. Weight does depending on the acceleration due to gravity.
Joe has a mass of 54 kg. What is his weight on the moon where the acceleration due to gravity is 1.62 m/s 2 ?
g = 1.62 m/s 2
F w = (54)(1.62) = 87.48 N
Joe has a mass of 54 kg. What is his weight on the earth?
g = 9.8 m/s 2
F w = (54)(9.8) = 529.2 N
Which changes depending on your location?
Mass (kg) never changes because it is a measure of the matter that you are composed of. You are the same matter on earth or on the moon.
Weight (F w ) changes when g changes. g changes depending on your altitude on earth, in space, or on another planet (it is not always 9.8 m/s 2 which is why many classes use a more rounded 10 m/s 2 instead.
Which is the term for the molecules that make up an object.
Matter is composed of the atoms/molecules that make up an object
What would happen to your weight if you were on a planet with twice the acceleration due to gravity?
Your score is
- Continue to Newton's Third Law
- Back to the Main Forces Page
- Back to the Stickman Physics Home Page
- Equation Sheet
Terms and Conditions - Privacy Policy
- Physics Formulas
Weight Formula

Weight is not anything but the force gravity experiences. It is represented by W and Newton is its SI unit. It is articulated as the product of mass and acceleration due to gravity. So the weight of a given object will show variation according to the gravity in that particular space. So, objects with similar mass appear in different weights across different planets.
Formula of Weight
The formula for weight is articulated as,
W=mg
- Weight of the object is W
- Mass of the object is m
- Acceleration due to gravity is g
Solved Examples
Numerical associated to weight calculations are provided underneath:
Problem 1: Compute the weight of a body on the moon if the mass is 60Kg? g is given as 1.625 m/s 2 . Answer :
It is known that, m = 60 kg and
g = 1.625 m/s 2
Formula for weight is, W = mg W = 60×1.625 W = 97.5 N
Problem 2: Compute the weight of a body on earth whose mass is 25 kg? Answer :
It is known that, m = 25 kg and
g = 9.8 m/s 2
Formula for weight is, W = mg W = 25×9.8 W = 245 N
| FORMULAS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
practice problem 1
Use the weight formula.
W = mg
Solve for mass. Substitute one newton for weight and one standard earth gravity for gravity.
| = | = | 1 N | ||
| 9.8 m/s | ||||
| = | 0.102 kg = 102 g | |||
The 96.7 gram tangerine comes closest to this value. Not all tangerines weigh 98.7 grams, however, so this is only a rule of thumb. There are certainly apples, bananas, oranges, tomatoes, and other fruits out there with a mass of approximately 102 grams and thus a weight of approximately one newton.
Those of you familiar with multiple choice tests should have eliminated the chicken egg as a possible answer. A chicken egg is only metaphorically the "fruit of the chicken".
practice problem 2
Here's the way I usually do it — using values I've memorized from years of use.
| = | |
| 2.2 lb = | (1 kg)(9.8 m/s ) |
| 1 lb = | 4.45… N |
Here's a more accurate way to do it — using values that are exact by definition.
| = | |
| 1 lb = | (0.45359237 kg)( ) |
| 1 lb = | 4.448221615… N |
Not quite a quarter pound, but you get the idea.
| 0.20 lb | < | 0.224808943… lb | < | 0.25 lb |
| ⅕ lb | < | 1 N | < | ¼ lb |
The fraction 9 40 gives a decimal expansion of 0.225, which is accurate to three significant figures. Not my favorite fraction, but it gets the job done. With sixteen avoirdupois ounces in a pound, one newton is also about 3½ ounces.
| 1 N ≈ | 9 lb | × | 16 oz | = | 18 oz | = 3½ oz |
| 40 | 1 lb | 5 |
practice problem 3
Practice problem 4.
5 Newton’s Laws of Motion
5.4 mass and weight, learning objectives.
By the end of the section, you will be able to:
- Explain the difference between mass and weight
- Explain why falling objects on Earth are never truly in free fall
- Describe the concept of weightlessness
Mass and weight are often used interchangeably in everyday conversation. For example, our medical records often show our weight in kilograms but never in the correct units of newtons. In physics, however, there is an important distinction. Weight is the pull of Earth on an object. It depends on the distance from the center of Earth. Unlike weight, mass does not vary with location. The mass of an object is the same on Earth, in orbit, or on the surface of the Moon.
Units of Force
The equation [latex] {F}_{\text{net}}=ma [/latex] is used to define net force in terms of mass, length, and time. As explained earlier, the SI unit of force is the newton. Since [latex] {F}_{\text{net}}=ma, [/latex]
Although almost the entire world uses the newton for the unit of force, in the United States, the most familiar unit of force is the pound (lb), where 1 N = 0.225 lb. Thus, a 225-lb person weighs 1000 N.
Weight and Gravitational Force
When an object is dropped, it accelerates toward the center of Earth. Newton’s second law says that a net force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, commonly called its weight [latex] \overset{\to }{w} [/latex], or its force due to gravity acting on an object of mass m . Weight can be denoted as a vector because it has a direction; down is, by definition, the direction of gravity, and hence, weight is a downward force. The magnitude of weight is denoted as w . Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the same acceleration g . Using Galileo’s result and Newton’s second law, we can derive an equation for weight.
Consider an object with mass m falling toward Earth. It experiences only the downward force of gravity, which is the weight [latex] \overset{\to }{w} [/latex]. Newton’s second law says that the magnitude of the net external force on an object is [latex] {\overset{\to }{F}}_{\text{net}}=m\overset{\to }{a}. [/latex] We know that the acceleration of an object due to gravity is [latex] \overset{\to }{g}, [/latex] or [latex] \overset{\to }{a}=\overset{\to }{g} [/latex]. Substituting these into Newton’s second law gives us the following equations.
The gravitational force on a mass is its weight. We can write this in vector form, where [latex] \overset{\to }{w} [/latex] is weight and m is mass, as
In scalar form, we can write
Since [latex] g=9.80\,{\text{m/s}}^{2} [/latex] on Earth, the weight of a 1.00-kg object on Earth is 9.80 N:
When the net external force on an object is its weight, we say that it is in free fall , that is, the only force acting on the object is gravity. However, when objects on Earth fall downward, they are never truly in free fall because there is always some upward resistance force from the air acting on the object.
Acceleration due to gravity g varies slightly over the surface of Earth, so the weight of an object depends on its location and is not an intrinsic property of the object. Weight varies dramatically if we leave Earth’s surface. On the Moon, for example, acceleration due to gravity is only [latex] {1.67\,\text{m/s}}^{2} [/latex]. A 1.0-kg mass thus has a weight of 9.8 N on Earth and only about 1.7 N on the Moon.
The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body, such as Earth, the Moon, or the Sun. This is the most common and useful definition of weight in physics. It differs dramatically, however, from the definition of weight used by NASA and the popular media in relation to space travel and exploration. When they speak of “weightlessness” and “microgravity,” they are referring to the phenomenon we call “free fall” in physics. We use the preceding definition of weight, force [latex] \overset{\to }{w} [/latex] due to gravity acting on an object of mass m , and we make careful distinctions between free fall and actual weightlessness.
Be aware that weight and mass are different physical quantities, although they are closely related. Mass is an intrinsic property of an object: It is a quantity of matter. The quantity or amount of matter of an object is determined by the numbers of atoms and molecules of various types it contains. Because these numbers do not vary, in Newtonian physics, mass does not vary; therefore, its response to an applied force does not vary. In contrast, weight is the gravitational force acting on an object, so it does vary depending on gravity. For example, a person closer to the center of Earth, at a low elevation such as New Orleans, weighs slightly more than a person who is located in the higher elevation of Denver, even though they may have the same mass.
It is tempting to equate mass to weight, because most of our examples take place on Earth, where the weight of an object varies only a little with the location of the object. In addition, it is difficult to count and identify all of the atoms and molecules in an object, so mass is rarely determined in this manner. If we consider situations in which [latex] \overset{\to }{g} [/latex] is a constant on Earth, we see that weight [latex] \overset{\to }{w} [/latex] is directly proportional to mass m , since [latex] \overset{\to }{w}=m\overset{\to }{g}, [/latex] that is, the more massive an object is, the more it weighs. Operationally, the masses of objects are determined by comparison with the standard kilogram, as we discussed in Units and Measurement . But by comparing an object on Earth with one on the Moon, we can easily see a variation in weight but not in mass. For instance, on Earth, a 5.0-kg object weighs 49 N; on the Moon, where g is [latex] {1.67\,\text{m/s}}^{2} [/latex], the object weighs 8.4 N. However, the mass of the object is still 5.0 kg on the Moon.
Clearing a Field
A farmer is lifting some moderately heavy rocks from a field to plant crops. He lifts a stone that weighs 40.0 lb. (about 180 N). What force does he apply if the stone accelerates at a rate of [latex] 1.5\,{\text{m/s}}^{2}? [/latex]
We were given the weight of the stone, which we use in finding the net force on the stone. However, we also need to know its mass to apply Newton’s second law, so we must apply the equation for weight, [latex] w=mg [/latex], to determine the mass.
No forces act in the horizontal direction, so we can concentrate on vertical forces, as shown in the following free-body diagram. We label the acceleration to the side; technically, it is not part of the free-body diagram, but it helps to remind us that the object accelerates upward (so the net force is upward).
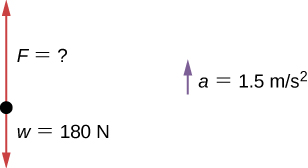
[latex] \begin{array}{ccc}\hfill w& =\hfill & mg\hfill \\ \hfill m& =\hfill & \frac{w}{g}=\frac{180\,\text{N}}{9.8\,{\text{m/s}}^{2}}=18\,\text{kg}\hfill \\ \hfill \sum F& =\hfill & ma\hfill \\ \hfill F-w& =\hfill & ma\hfill \\ \hfill F-180\,\text{N}& =\hfill & (18\,\text{kg})(1.5\,{\text{m/s}}^{2})\hfill \\ \hfill F-180\,\text{N}& =\hfill & 27\,\text{N}\hfill \\ \hfill F& =\hfill & 207\,\text{N}=210\,\text{N to two significant figures}\hfill \end{array} [/latex]
Significance
To apply Newton’s second law as the primary equation in solving a problem, we sometimes have to rely on other equations, such as the one for weight or one of the kinematic equations, to complete the solution.
Check Your Understanding
For (Example) , find the acceleration when the farmer’s applied force is 230.0 N.
[latex] a=2.78\,{\text{m/s}}^{2} [/latex]
Can you avoid the boulder field and land safely just before your fuel runs out, as Neil Armstrong did in 1969? This version of the classic video game accurately simulates the real motion of the lunar lander, with the correct mass, thrust, fuel consumption rate, and lunar gravity. The real lunar lander is hard to control.
Use this interactive simulation to move the Sun, Earth, Moon, and space station to see the effects on their gravitational forces and orbital paths. Visualize the sizes and distances between different heavenly bodies, and turn off gravity to see what would happen without it.
- Mass is the quantity of matter in a substance.
- The weight of an object is the net force on a falling object, or its gravitational force. The object experiences acceleration due to gravity.
- Some upward resistance force from the air acts on all falling objects on Earth, so they can never truly be in free fall.
- Careful distinctions must be made between free fall and weightlessness using the definition of weight as force due to gravity acting on an object of a certain mass.
Conceptual Questions
What is the relationship between weight and mass? Which is an intrinsic, unchanging property of a body?
How much does a 70-kg astronaut weight in space, far from any celestial body? What is her mass at this location?
The astronaut is truly weightless in the location described, because there is no large body (planet or star) nearby to exert a gravitational force. Her mass is 70 kg regardless of where she is located.
Which of the following statements is accurate?
(a) Mass and weight are the same thing expressed in different units.
(b) If an object has no weight, it must have no mass.
(c) If the weight of an object varies, so must the mass.
(d) Mass and inertia are different concepts.
(e) Weight is always proportional to mass.
When you stand on Earth, your feet push against it with a force equal to your weight. Why doesn’t Earth accelerate away from you?
The force you exert (a contact force equal in magnitude to your weight) is small. Earth is extremely massive by comparison. Thus, the acceleration of Earth would be incredibly small. To see this, use Newton’s second law to calculate the acceleration you would cause if your weight is 600.0 N and the mass of Earth is [latex] 6.00\,×\,{10}^{24}\,\text{kg} [/latex].
How would you give the value of [latex] \overset{\to }{g} [/latex] in vector form?
The weight of an astronaut plus his space suit on the Moon is only 250 N. (a) How much does the suited astronaut weigh on Earth? (b) What is the mass on the Moon? On Earth?
a. [latex] \begin{array}{ccc}\hfill {w}_{\text{Moon}}& =\hfill & m{g}_{\text{Moon}}\hfill \\ \hfill m& =\hfill & 150\,\text{kg}\hfill \\ \hfill {w}_{\text{Earth}}& =\hfill & 1.5\,×\,{10}^{3}\,\text{N}\hfill \end{array} [/latex]; b. Mass does not change, so the suited astronaut’s mass on both Earth and the Moon is [latex] 150\,\text{kg.} [/latex]
Suppose the mass of a fully loaded module in which astronauts take off from the Moon is [latex] 1.00\,×\,{10}^{4} [/latex] kg. The thrust of its engines is [latex] 3.00\,×\,{10}^{4} [/latex] N. (a) Calculate the module’s magnitude of acceleration in a vertical takeoff from the Moon. (b) Could it lift off from Earth? If not, why not? If it could, calculate the magnitude of its acceleration.
A rocket sled accelerates at a rate of [latex] {49.0\,\text{m/s}}^{2} [/latex]. Its passenger has a mass of 75.0 kg. (a) Calculate the horizontal component of the force the seat exerts against his body. Compare this with his weight using a ratio. (b) Calculate the direction and magnitude of the total force the seat exerts against his body.
a. [latex] \begin{array}{ccc}\hfill {F}_{\text{h}}& =\hfill & 3.68\,×\,{10}^{3}\,\text{N and}\hfill \\ \hfill w& =\hfill & 7.35\,×\,{10}^{2}\,\text{N}\hfill \\ \hfill \frac{{F}_{\text{h}}}{w}& =\hfill & 5.00\,\text{times greater than weight}\hfill \end{array} [/latex];
b. [latex] \begin{array}{ccc}\hfill {F}_{\text{net}}& =\hfill & 3750\,\text{N}\hfill \\ \hfill \theta & =\hfill & 11.3\text{°}\,\text{from horizontal}\hfill \end{array} [/latex]
Repeat the previous problem for a situation in which the rocket sled decelerates at a rate of [latex] {201\,\text{m/s}}^{2} [/latex]. In this problem, the forces are exerted by the seat and the seat belt.
A body of mass 2.00 kg is pushed straight upward by a 25.0 N vertical force. What is its acceleration?
[latex] \begin{array}{ccc}\hfill w& =\hfill & 19.6\,\text{N}\hfill \\ \hfill {F}_{\text{net}}& =\hfill & 5.40\,\text{N}\hfill \\ \hfill {F}_{\text{net}}& =\hfill & ma⇒a=2.70\,{\text{m/s}}^{2}\hfill \end{array} [/latex]
A car weighing 12,500 N starts from rest and accelerates to 83.0 km/h in 5.00 s. The friction force is 1350 N. Find the applied force produced by the engine.
A body with a mass of 10.0 kg is assumed to be in Earth’s gravitational field with [latex] g=9.80\,{\text{m/s}}^{2} [/latex]. What is its acceleration?
[latex] 0.60\hat{i}-8.4\hat{j}\,{\text{m/s}}^{2} [/latex]
A fireman has mass m ; he hears the fire alarm and slides down the pole with acceleration a (which is less than g in magnitude). (a) Write an equation giving the vertical force he must apply to the pole. (b) If his mass is 90.0 kg and he accelerates at [latex] 5.00\,{\text{m/s}}^{2}, [/latex] what is the magnitude of his applied force?
A baseball catcher is performing a stunt for a television commercial. He will catch a baseball (mass 145 g) dropped from a height of 60.0 m above his glove. His glove stops the ball in 0.0100 s. What is the force exerted by his glove on the ball?
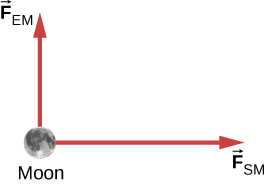
When the Moon is directly overhead at sunset, the force by Earth on the Moon, [latex] {F}_{\text{EM}} [/latex], is essentially at [latex] 90\text{°} [/latex] to the force by the Sun on the Moon, [latex] {F}_{\text{SM}} [/latex], as shown below. Given that [latex] {F}_{\text{EM}}=1.98\,×\,{10}^{20}\,\text{N} [/latex] and [latex] {F}_{\text{SM}}=4.36\,×\,{10}^{20}\,\text{N}, [/latex] all other forces on the Moon are negligible, and the mass of the Moon is [latex] 7.35\,×\,{10}^{22}\,\text{kg}, [/latex] determine the magnitude of the Moon’s acceleration.
- OpenStax University Physics. Authored by : OpenStax CNX. Located at : https://cnx.org/contents/[email protected]:Gofkr9Oy@15 . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy
Worksheet on Word Problem on Measuring Mass
Practice the questions given in the worksheet on word problem on measuring mass (i.e. addition and subtraction). Addition and subtraction in grams and kilograms is done in the similar way as in the case of ordinary numbers.
1. Jason purchased 7 kg 200 g of sugar, 9 kg 395 g of rice. What is the total weight which Jason carried?
2. Rachel bought 8 kg 400 g tomatoes, 2 kg 130 g brinjal and 7 kg 300 g watermelon from the green grocer. How many kilograms of fruits and vegetables did she buy?
3. A rickshaw-puller is carrying two persons weighting 52 kg 250 g and 37 kg 700 g. What is the total weight of the two persons carried by the rickshaw-puller?
4. The total weight of Tania’s bag is 45 kg 750 g and Diana’s bag is 43 kg 950 g. Whose bag is heavier and by how much?
5. A truck was loaded with 352 kg 100 g of pumpkins and 207 kg 432 g of watermelons. Find the total weight carried by the truck.
6. Weight of a pile of English newspaper is 16 kg 270 g and that of French newspaper is 18 kg 227 g. If both the piles are tied together, what will be the total weight of the bundle?
7. A shopkeeper sold 67 kg 626 g of wheat on Saturday and 125 kg 200 g of wheat on Sunday. Find the total weight of wheat sold on both the days.
8. A grocer puts apples and plums together on the weighing machine. The total weight shown on the machine is 8 kg. If the weight of the plums is 2 kg 700 g, then what is the weight of the apples?
9. Jasmine purchased 7 kg 302 g of rice and Melissa purchased 3 kg 598 g more. What quantity of rice did Jasmine and Melissa purchase?
10. The weight of a chocolate carton is 20 kg. Each carton has 10 packets. Each packet has 25 chocolates. How many chocolates are there? Find the weight of each chocolate presuming that weight of carton and packets is negligible.
11. Brian sold 123 kg 231 g of newspapers and 200 kg of magazines. Find the total quantity of articles sold.
12. Ron takes care of deer and wild bulls in the zoo. The deer weighs 182 kg 290 g and a wild bull weighs 753 kg 380 g. Answer the given questions.
(i) If the both the animals stand on a weighing machine together what will be the total weight shown on the machine?
(ii) By how much is a bull heavier than deer?
(iii) If a deer eats 15 kg 250 g grass in a week. How much grass will be eaten by a deer in 42 days?
13. Aaron weight 49 kg 357 g and Ron weights 32 kg 458 g. Who weighs less and by how much?
14. If the total weight of 24 bulls having same weight is 487200 kg. What is the weight of each bull?
15. Father bought 10 kg 750 g of fruits (mangoes and apples). He had 6 kg 860 g of mangoes. What is the weight of apples?
16. Nina bought 5 kg of fruits. On the way home, she ate 750 g of fruits. How much fruit did she take back home?
17. Nancy brought a cake weighing 5 kg 675 g. Approximately 2 kg 395 g of cake is distributed among the children. What quantity of cake is left?
18. Rita weighs 13 kg 250 g. Her elder brother is three times heavier than Rita. What is her brother’s weight?
19. Mother purchased 9 kg 357 g of sweets and snacks for the occasion. Out of which 6 kg 458 g were consumed. What quantity of sweets and snacks were left?
20. A box can carry a total weight of 27 kg. Candies have to be packed inside the box. If the weight of each candy is 30 g, how many candies can be packed inside the box?
21. A shopkeeper purchased 287 kg 500 g of orange. Later on, he found that 98 kg 300 g of oranges were rotten. Find the quantity of oranges in good condition.
22. A lift can withstand a weight of 500 kg. There are 7 people standing to go in the lift. Given below are their weights. Find out if all of them can go inside the lift altogether. If no, then why?

23. Mary weighs 63 kg 59 g and Alex weighs 59 kg 36 g. Who weighs less and by how much?
24. Kellie’s weight is 55 kg 330 g. The doctor says that according to her height, her weight should be 62 kg. How much weight should she gain?
25. How much heavier is the toffee packet which has mass 1 kg 845 g in comparison to 500 g of chocolates?
Answers for the worksheet on word problem on measuring mass (i.e. addition and subtraction) are given below.
1. 16 kg 595 g
2. 17 kg 830 g
3. 89 kg 950 g
4. Tania’s bag is 1 kg 800 g
5. 559 kg 532 g
6. 34 kg 497 g
7. 192 kg 826 g
8. 5 kg 300 g
9. 10 kg 900 g
10. 250, 80 g
11. 323 kg 231 g
12. (i) 935 kg 670 g
(ii) 571 kg 90 g
(iii) 91 kg 500 g
13. Ron weighs less by 16 kg 899 g
14. 20,300 kg
15. 3 kg 890 g
16. 4 kg 250 g
17. 3 kg 280 g
18. 39 kg 750 g
19. 2 kg 899 g

21. 189 kg 200 g
22. All can go, 425 kg 350 g
23. Alex weighs less by 4 kg 23 g
24. 6 kg 670 g
25. 1 kg 345 g
Measurement of Mass:
What is Mass?
Conversion of Standard Unit of Mass
Conversion of Measuring Mass
Addition of Mass
Subtraction of Mass
Addition and Subtraction of Measuring Mass
Worksheet on Conversion of Mass
Worksheet on Addition of Mass
Worksheet on Third Grade Measurement of Mass
Worksheet on Subtraction of Mass
3rd Grade Math Worksheets
3rd Grade Math Lessons
From Worksheet on Word Problem on Measuring Mass to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Subtracting 2-digit numbers | how to subtract two digit numbers.
Sep 27, 24 05:04 PM

Properties of Subtraction |Whole Numbers |Subtraction of Whole Numbers
Sep 26, 24 02:54 PM
Subtraction of Numbers using Number Line |Subtracting with Number Line
Sep 26, 24 12:42 PM
2nd Grade Subtraction Worksheet | Subtraction of 2-Digit Numbers | Ans
Sep 25, 24 04:37 PM
3rd Grade Addition Worksheet | 3-Digit Addition | Word Problems | Ans
Sep 25, 24 01:32 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

The Math You Need, When You Need It
math tutorials for students in introductory geoscience
- First Publication: July 19, 2011
- Revision: September 19, 2024 -- Updated website to improve accessibility of images math equations and chrome.
Density and Specific Gravity - Practice Problems
Jump to: Rock and Mineral density | Rock and mineral specific gravity You can download the questions (Acrobat (PDF) 25kB Jul24 09) if you would like to work them on a separate sheet of paper.
Calculating Densities of Rocks and Minerals

`Volume\times Density=Mass` You can then divide both sides by density to get volume alone: `Volume=\frac{Mass}{Density}` By substituting in the values listed above, `Volume=\frac{2000\ kg}{3200\ \frac{kg}{m^{3}}}`
so the volume will be 0.625 m 3 Note that the above problem shows that densities can be in units other than grams and cubic centimeters. To avoid the potential problems of different units, many geologists use specific gravity (SG), explored in problems 8 and 9, below.

`text{volume}=text{length}\times text{width}\times text{height}` .
The volume of the cube is
`2cm\times2cm\times2cm=8cm^{3}` . The density then is the mass divided by the volume: `Density=\frac{Mass}{Volume}` `Density=\frac{40g}{8cm^{3}}=5.0\frac{g}{cm^{3}}` Thus the cube is NOT gold , since the density (5.0 g/cm 3 ) is not the same as gold (19.3 g/cm 3 ). You tell the seller to take a hike . You might even notice that the density of pyrite (a.k.a. fool's gold) is 5.0 g/cm 3 . Luckily you are no fool and know about density!
Calculating Specific Gravity of Rocks and Minerals
Take the quiz .
If this is not how you feel, you can go back to the explanations .
« Previous Page Next Page »
- TPC and eLearning
- What's NEW at TPC?
- Read Watch Interact
- Practice Review Test
- Teacher-Tools
- Request a Demo
- Get A Quote
- Subscription Selection
- Seat Calculator
- Ad Free Account
- Edit Profile Settings
- Metric Conversions Questions
- Metric System Questions
- Metric Estimation Questions
- Significant Digits Questions
- Proportional Reasoning
- Acceleration
- Distance-Displacement
- Dots and Graphs
- Graph That Motion
- Match That Graph
- Name That Motion
- Motion Diagrams
- Pos'n Time Graphs Numerical
- Pos'n Time Graphs Conceptual
- Up And Down - Questions
- Balanced vs. Unbalanced Forces
- Change of State
- Force and Motion
Mass and Weight
- Match That Free-Body Diagram
- Net Force (and Acceleration) Ranking Tasks
- Newton's Second Law
- Normal Force Card Sort
- Recognizing Forces
- Air Resistance and Skydiving
- Solve It! with Newton's Second Law
- Which One Doesn't Belong?
- Component Addition Questions
- Head-to-Tail Vector Addition
- Projectile Mathematics
- Trajectory - Angle Launched Projectiles
- Trajectory - Horizontally Launched Projectiles
- Vector Addition
- Vector Direction
- Which One Doesn't Belong? Projectile Motion
- Forces in 2-Dimensions
- Being Impulsive About Momentum
- Explosions - Law Breakers
- Hit and Stick Collisions - Law Breakers
- Case Studies: Impulse and Force
- Impulse-Momentum Change Table
- Keeping Track of Momentum - Hit and Stick
- Keeping Track of Momentum - Hit and Bounce
- What's Up (and Down) with KE and PE?
- Energy Conservation Questions
- Energy Dissipation Questions
- Energy Ranking Tasks
- LOL Charts (a.k.a., Energy Bar Charts)
- Match That Bar Chart
- Words and Charts Questions
- Name That Energy
- Stepping Up with PE and KE Questions
- Case Studies - Circular Motion
- Circular Logic
- Forces and Free-Body Diagrams in Circular Motion
- Gravitational Field Strength
- Universal Gravitation
- Angular Position and Displacement
- Linear and Angular Velocity
- Angular Acceleration
- Rotational Inertia
- Balanced vs. Unbalanced Torques
- Getting a Handle on Torque
- Torque-ing About Rotation
- Properties of Matter
- Fluid Pressure
- Buoyant Force
- Sinking, Floating, and Hanging
- Pascal's Principle
- Flow Velocity
- Bernoulli's Principle
- Balloon Interactions
- Charge and Charging
- Charge Interactions
- Charging by Induction
- Conductors and Insulators
- Coulombs Law
- Electric Field
- Electric Field Intensity
- Polarization
- Case Studies: Electric Power
- Know Your Potential
- Light Bulb Anatomy
- I = ∆V/R Equations as a Guide to Thinking
- Parallel Circuits - ∆V = I•R Calculations
- Resistance Ranking Tasks
- Series Circuits - ∆V = I•R Calculations
- Series vs. Parallel Circuits
- Equivalent Resistance
- Period and Frequency of a Pendulum
- Pendulum Motion: Velocity and Force
- Energy of a Pendulum
- Period and Frequency of a Mass on a Spring
- Horizontal Springs: Velocity and Force
- Vertical Springs: Velocity and Force
- Energy of a Mass on a Spring
- Decibel Scale
- Frequency and Period
- Closed-End Air Columns
- Name That Harmonic: Strings
- Rocking the Boat
- Wave Basics
- Matching Pairs: Wave Characteristics
- Wave Interference
- Waves - Case Studies
- Color Addition and Subtraction
- Color Filters
- If This, Then That: Color Subtraction
- Light Intensity
- Color Pigments
- Converging Lenses
- Curved Mirror Images
- Law of Reflection
- Refraction and Lenses
- Total Internal Reflection
- Who Can See Who?
- Lab Equipment
- Lab Procedures
- Formulas and Atom Counting
- Atomic Models
- Bond Polarity
- Entropy Questions
- Cell Voltage Questions
- Heat of Formation Questions
- Reduction Potential Questions
- Oxidation States Questions
- Measuring the Quantity of Heat
- Hess's Law
- Oxidation-Reduction Questions
- Galvanic Cells Questions
- Thermal Stoichiometry
- Molecular Polarity
- Quantum Mechanics
- Balancing Chemical Equations
- Bronsted-Lowry Model of Acids and Bases
- Classification of Matter
- Collision Model of Reaction Rates
- Density Ranking Tasks
- Dissociation Reactions
- Complete Electron Configurations
- Elemental Measures
- Enthalpy Change Questions
- Equilibrium Concept
- Equilibrium Constant Expression
- Equilibrium Calculations - Questions
- Equilibrium ICE Table
- Intermolecular Forces Questions
- Ionic Bonding
- Lewis Electron Dot Structures
- Limiting Reactants
- Line Spectra Questions
- Mass Stoichiometry
- Measurement and Numbers
- Metals, Nonmetals, and Metalloids
- Metric Estimations
- Metric System
- Molarity Ranking Tasks
- Mole Conversions
- Name That Element
- Names to Formulas
- Names to Formulas 2
- Nuclear Decay
- Particles, Words, and Formulas
- Periodic Trends
- Precipitation Reactions and Net Ionic Equations
- Pressure Concepts
- Pressure-Temperature Gas Law
- Pressure-Volume Gas Law
- Chemical Reaction Types
- Significant Digits and Measurement
- States Of Matter Exercise
- Stoichiometry Law Breakers
- Stoichiometry - Math Relationships
- Subatomic Particles
- Spontaneity and Driving Forces
- Gibbs Free Energy
- Volume-Temperature Gas Law
- Acid-Base Properties
- Energy and Chemical Reactions
- Chemical and Physical Properties
- Valence Shell Electron Pair Repulsion Theory
- Writing Balanced Chemical Equations
- Mission CG1
- Mission CG10
- Mission CG2
- Mission CG3
- Mission CG4
- Mission CG5
- Mission CG6
- Mission CG7
- Mission CG8
- Mission CG9
- Mission EC1
- Mission EC10
- Mission EC11
- Mission EC12
- Mission EC2
- Mission EC3
- Mission EC4
- Mission EC5
- Mission EC6
- Mission EC7
- Mission EC8
- Mission EC9
- Mission RL1
- Mission RL2
- Mission RL3
- Mission RL4
- Mission RL5
- Mission RL6
- Mission KG7
- Mission RL8
- Mission KG9
- Mission RL10
- Mission RL11
- Mission RM1
- Mission RM2
- Mission RM3
- Mission RM4
- Mission RM5
- Mission RM6
- Mission RM8
- Mission RM10
- Mission LC1
- Mission RM11
- Mission LC2
- Mission LC3
- Mission LC4
- Mission LC5
- Mission LC6
- Mission LC8
- Mission SM1
- Mission SM2
- Mission SM3
- Mission SM4
- Mission SM5
- Mission SM6
- Mission SM8
- Mission SM10
- Mission KG10
- Mission SM11
- Mission KG2
- Mission KG3
- Mission KG4
- Mission KG5
- Mission KG6
- Mission KG8
- Mission KG11
- Mission F2D1
- Mission F2D2
- Mission F2D3
- Mission F2D4
- Mission F2D5
- Mission F2D6
- Mission KC1
- Mission KC2
- Mission KC3
- Mission KC4
- Mission KC5
- Mission KC6
- Mission KC7
- Mission KC8
- Mission AAA
- Mission SM9
- Mission LC7
- Mission LC9
- Mission NL1
- Mission NL2
- Mission NL3
- Mission NL4
- Mission NL5
- Mission NL6
- Mission NL7
- Mission NL8
- Mission NL9
- Mission NL10
- Mission NL11
- Mission NL12
- Mission MC1
- Mission MC10
- Mission MC2
- Mission MC3
- Mission MC4
- Mission MC5
- Mission MC6
- Mission MC7
- Mission MC8
- Mission MC9
- Mission RM7
- Mission RM9
- Mission RL7
- Mission RL9
- Mission SM7
- Mission SE1
- Mission SE10
- Mission SE11
- Mission SE12
- Mission SE2
- Mission SE3
- Mission SE4
- Mission SE5
- Mission SE6
- Mission SE7
- Mission SE8
- Mission SE9
- Mission VP1
- Mission VP10
- Mission VP2
- Mission VP3
- Mission VP4
- Mission VP5
- Mission VP6
- Mission VP7
- Mission VP8
- Mission VP9
- Mission WM1
- Mission WM2
- Mission WM3
- Mission WM4
- Mission WM5
- Mission WM6
- Mission WM7
- Mission WM8
- Mission WE1
- Mission WE10
- Mission WE2
- Mission WE3
- Mission WE4
- Mission WE5
- Mission WE6
- Mission WE7
- Mission WE8
- Mission WE9
- Vector Walk Interactive
- Name That Motion Interactive
- Kinematic Graphing 1 Concept Checker
- Kinematic Graphing 2 Concept Checker
- Graph That Motion Interactive
- Two Stage Rocket Interactive
- Rocket Sled Concept Checker
- Force Concept Checker
- Free-Body Diagrams Concept Checker
- Free-Body Diagrams The Sequel Concept Checker
- Skydiving Concept Checker
- Elevator Ride Concept Checker
- Vector Addition Concept Checker
- Vector Walk in Two Dimensions Interactive
- Name That Vector Interactive
- River Boat Simulator Concept Checker
- Projectile Simulator 2 Concept Checker
- Projectile Simulator 3 Concept Checker
- Hit the Target Interactive
- Turd the Target 1 Interactive
- Turd the Target 2 Interactive
- Balance It Interactive
- Go For The Gold Interactive
- Egg Drop Concept Checker
- Fish Catch Concept Checker
- Exploding Carts Concept Checker
- Collision Carts - Inelastic Collisions Concept Checker
- Its All Uphill Concept Checker
- Stopping Distance Concept Checker
- Chart That Motion Interactive
- Roller Coaster Model Concept Checker
- Uniform Circular Motion Concept Checker
- Horizontal Circle Simulation Concept Checker
- Vertical Circle Simulation Concept Checker
- Race Track Concept Checker
- Gravitational Fields Concept Checker
- Orbital Motion Concept Checker
- Angular Acceleration Concept Checker
- Balance Beam Concept Checker
- Torque Balancer Concept Checker
- Aluminum Can Polarization Concept Checker
- Charging Concept Checker
- Name That Charge Simulation
- Coulomb's Law Concept Checker
- Electric Field Lines Concept Checker
- Put the Charge in the Goal Concept Checker
- Circuit Builder Concept Checker (Series Circuits)
- Circuit Builder Concept Checker (Parallel Circuits)
- Circuit Builder Concept Checker (∆V-I-R)
- Circuit Builder Concept Checker (Voltage Drop)
- Equivalent Resistance Interactive
- Pendulum Motion Simulation Concept Checker
- Mass on a Spring Simulation Concept Checker
- Particle Wave Simulation Concept Checker
- Boundary Behavior Simulation Concept Checker
- Slinky Wave Simulator Concept Checker
- Simple Wave Simulator Concept Checker
- Wave Addition Simulation Concept Checker
- Standing Wave Maker Simulation Concept Checker
- Color Addition Concept Checker
- Painting With CMY Concept Checker
- Stage Lighting Concept Checker
- Filtering Away Concept Checker
- InterferencePatterns Concept Checker
- Young's Experiment Interactive
- Plane Mirror Images Interactive
- Who Can See Who Concept Checker
- Optics Bench (Mirrors) Concept Checker
- Name That Image (Mirrors) Interactive
- Refraction Concept Checker
- Total Internal Reflection Concept Checker
- Optics Bench (Lenses) Concept Checker
- Kinematics Preview
- Velocity Time Graphs Preview
- Moving Cart on an Inclined Plane Preview
- Stopping Distance Preview
- Cart, Bricks, and Bands Preview
- Fan Cart Study Preview
- Friction Preview
- Coffee Filter Lab Preview
- Friction, Speed, and Stopping Distance Preview
- Up and Down Preview
- Projectile Range Preview
- Ballistics Preview
- Juggling Preview
- Marshmallow Launcher Preview
- Air Bag Safety Preview
- Colliding Carts Preview
- Collisions Preview
- Engineering Safer Helmets Preview
- Push the Plow Preview
- Its All Uphill Preview
- Energy on an Incline Preview
- Modeling Roller Coasters Preview
- Hot Wheels Stopping Distance Preview
- Ball Bat Collision Preview
- Energy in Fields Preview
- Weightlessness Training Preview
- Roller Coaster Loops Preview
- Universal Gravitation Preview
- Keplers Laws Preview
- Kepler's Third Law Preview
- Charge Interactions Preview
- Sticky Tape Experiments Preview
- Wire Gauge Preview
- Voltage, Current, and Resistance Preview
- Light Bulb Resistance Preview
- Series and Parallel Circuits Preview
- Thermal Equilibrium Preview
- Linear Expansion Preview
- Heating Curves Preview
- Electricity and Magnetism - Part 1 Preview
- Electricity and Magnetism - Part 2 Preview
- Vibrating Mass on a Spring Preview
- Period of a Pendulum Preview
- Wave Speed Preview
- Slinky-Experiments Preview
- Standing Waves in a Rope Preview
- Sound as a Pressure Wave Preview
- DeciBel Scale Preview
- DeciBels, Phons, and Sones Preview
- Sound of Music Preview
- Shedding Light on Light Bulbs Preview
- Models of Light Preview
- Electromagnetic Radiation Preview
- Electromagnetic Spectrum Preview
- EM Wave Communication Preview
- Digitized Data Preview
- Light Intensity Preview
- Concave Mirrors Preview
- Object Image Relations Preview
- Snells Law Preview
- Reflection vs. Transmission Preview
- Magnification Lab Preview
- Reactivity Preview
- Ions and the Periodic Table Preview
- Periodic Trends Preview
- Chemical Reactions Preview
- Intermolecular Forces Preview
- Melting Points and Boiling Points Preview
- Bond Energy and Reactions Preview
- Reaction Rates Preview
- Ammonia Factory Preview
- Stoichiometry Preview
- Nuclear Chemistry Preview
- Gaining Teacher Access
- Task Tracker Directions
- Conceptual Physics Course
- On-Level Physics Course
- Honors Physics Course
- Chemistry Concept Builders
- All Chemistry Resources
- Users Voice
- Tasks and Classes
- Webinars and Trainings
- Subscription
- Subscription Locator
- 1-D Kinematics
- Newton's Laws
- Vectors - Motion and Forces in Two Dimensions
- Momentum and Its Conservation
- Work and Energy
- Circular Motion and Satellite Motion
- Thermal Physics
- Static Electricity
- Electric Circuits
- Vibrations and Waves
- Sound Waves and Music
- Light and Color
- Reflection and Mirrors
- Measurement and Calculations
- Elements, Atoms, and Ions
- Compounds,Names, and Formulas
- About the Physics Interactives
- Task Tracker
- Usage Policy
- Newtons Laws
- Vectors and Projectiles
- Forces in 2D
- Momentum and Collisions
- Circular and Satellite Motion
- Balance and Rotation
- Electromagnetism
- Waves and Sound
- Atomic Physics
- Forces in Two Dimensions
- Work, Energy, and Power
- Circular Motion and Gravitation
- Sound Waves
- 1-Dimensional Kinematics
- Circular, Satellite, and Rotational Motion
- Einstein's Theory of Special Relativity
- Waves, Sound and Light
- QuickTime Movies
- About the Concept Builders
- Pricing For Schools
- Directions for Version 2
- Measurement and Units
- Relationships and Graphs
- Rotation and Balance
- Vibrational Motion
- Reflection and Refraction
- Teacher Accounts
- Kinematic Concepts
- Kinematic Graphing
- Wave Motion
- Sound and Music
- About CalcPad
- 1D Kinematics
- Vectors and Forces in 2D
- Simple Harmonic Motion
- Rotational Kinematics
- Rotation and Torque
- Rotational Dynamics
- Electric Fields, Potential, and Capacitance
- Transient RC Circuits
- Light Waves
- Units and Measurement
- Stoichiometry
- Molarity and Solutions
- Thermal Chemistry
- Acids and Bases
- Kinetics and Equilibrium
- Solution Equilibria
- Oxidation-Reduction
- Nuclear Chemistry
- Newton's Laws of Motion
- Work and Energy Packet
- Static Electricity Review
- NGSS Alignments
- 1D-Kinematics
- Projectiles
- Circular Motion
- Magnetism and Electromagnetism
- Graphing Practice
- About the ACT
- ACT Preparation
- For Teachers
- Other Resources
- Solutions Guide
- Solutions Guide Digital Download
- Motion in One Dimension
- Work, Energy and Power
- Chemistry of Matter
- Measurement and the Metric System
- Names and Formulas
- Algebra Based On-Level Physics
- Honors Physics
- Conceptual Physics
- Other Tools
- Frequently Asked Questions
- Purchasing the Download
- Purchasing the Digital Download
- About the NGSS Corner
- NGSS Search
- Force and Motion DCIs - High School
- Energy DCIs - High School
- Wave Applications DCIs - High School
- Force and Motion PEs - High School
- Energy PEs - High School
- Wave Applications PEs - High School
- Crosscutting Concepts
- The Practices
- Physics Topics
- NGSS Corner: Activity List
- NGSS Corner: Infographics
- About the Toolkits
- Position-Velocity-Acceleration
- Position-Time Graphs
- Velocity-Time Graphs
- Newton's First Law
- Newton's Second Law
- Newton's Third Law
- Terminal Velocity
- Projectile Motion
- Forces in 2 Dimensions
- Impulse and Momentum Change
- Momentum Conservation
- Work-Energy Fundamentals
- Work-Energy Relationship
- Roller Coaster Physics
- Satellite Motion
- Electric Fields
- Circuit Concepts
- Series Circuits
- Parallel Circuits
- Describing-Waves
- Wave Behavior Toolkit
- Standing Wave Patterns
- Resonating Air Columns
- Wave Model of Light
- Plane Mirrors
- Curved Mirrors
- Teacher Guide
- Using Lab Notebooks
- Current Electricity
- Light Waves and Color
- Reflection and Ray Model of Light
- Refraction and Ray Model of Light
- Teacher Resources
- Subscriptions

- Newton's Laws
- Einstein's Theory of Special Relativity
- About Concept Checkers
- School Pricing
- Newton's Laws of Motion
- Newton's First Law
- Newton's Third Law
Launch Concept Builder
Lesson resources
Starter quiz questions
Starter quiz answers
Exit quiz questions
Exit quiz answers
Your details
Lesson Streak

Learn Spelling
Learn grammar, learn handwriting.

Weighted Average Problems
In these lessons, we will learn how to solve weighted average problems.
Related Pages Mean, Median, Mode, Range Other Algebra Word Problems
There are three main types of average problems commonly encountered in school algebra: Average (Arithmetic Mean) , Weighted Average and Average Speed .
The following table gives the formulas for average problems: Weighted Average, Mean, and Average Speed. Scroll down the page for examples and solutions.

We have lots of free Printable and Online Statistics Worksheets for you to review and practice your skills in Statistics.
One type of average problems involves the weighted average - which is the average of two or more terms that do not all have the same number of members. To find the weighted term, multiply each term by its weighting factor, which is the number of times each term occurs.
The formula for weighted average is:
Example: A class of 25 students took a science test. 10 students had an average (arithmetic mean) score of 80. The other students had an average score of 60. What is the average score of the whole class?
Solution: Step 1: To get the sum of weighted terms, multiply each average by the number of students that had that average and then sum them up.
80 × 10 + 60 × 15 = 800 + 900 = 1700
Step 2: Total number of terms = Total number of students = 25
Step 3: Using the formula,
Answer: The average score of the whole class is 68.
Be careful! You will get the wrong answer if you add the two average scores and divide the answer by two.
Example of how to calculate the weighted average
Example: At a health club, 80% of the members are men and 20% of the members are women. If the average age of the men is 30 and the average age of the women is 40, what is the average age of all the members?
How to find the weighted average given a frequency table?
Example: A group of people were surveyed for how many movies they see in a week. The table below shows the result of the survey. (a) How many people took part in the survey? (b) What was the total number of movies seen in a week by all the survey takers? (c) What was the average number of movies seen in a week per person surveyed?
How to solve Weighted Averages and Mixture Problems? Mixture problems are problems in which two or more parts are combined into a whole.
- Premium coffee is $9.50/lb, Supreme coffee is $11.75/lb and Blend coffee is $10.00/lb. How many pounds of Premium coffee beans should be mixed with two pounds of Supreme coffee to make Blend coffee?
- A car’s radiator should contain a solution of 50% antifreeze. Bo has 2 gallons of 35% antifreeze. How many gallons of 100% antifreeze should he add to his solution to produce a solution of 50% antifreeze?
How to solve Weighted Average Word Problems?
- How many pounds of mixed nuts selling for $4.75 per pound should be mixed with 10 pounds of dried fruit selling for $5.50 per pound to obtain a trail mix that sells for $4.95 per pound?
- A chemistry experiment calls for a 30% solution of copper sulfate. Kendra has 40 milliliters of 25% solution. How many milliliters of 60% solution should she add to make a 30% solution?
- A car and an emergency are heading toward each other. The car is traveling at a speed of 30 mph or 44 feet per second. The emergency vehicle is traveling at a speed of 50 mph or about 74 feet per second. If the vehicles are 1000 feet apart and the conditions are ideal, in how many seconds will the drive of the car first hear the siren?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
These are our mass and weight Word Problems worksheets for 2nd grade math school. Click on the previews to go to download page.
Worksheet by math grade levels:
Our grade 2 math worksheets are free and printable in PDF format. Based on the Singaporean math curriculum for second graders, these math worksheets are made for students in grade level 2. However, also students in other grade levels can benefit from doing these math worksheets. Feel free to print them. Our math worksheets cover important math topics such as: whole numbers, spelling, place value, skip counting, addition and subtraction, multiplication tables, basic division facts, fractions, mixed operations, geometry, graphing, picture graphs, measurement of time, mass, length and volume.
Our first grade math worksheets are free and printable in PDF format. Based on the Singaporean math school curriculum for grade 1 students, these 1st level math worksheets are made for students in school, tutoring or online math education. Our grade 1 math worksheets cover topics such as: whole numbers, spelling of basic numbers up to 10 or 100 and first grade math operations, grade 1addition and subtraction, place value, skip counting, introduction to division and multiplication, first grade geometry and basic shapes, easy picture graphs, length, volume and mass measurement and beginners number patterns.
WORD PROBLEMS INVOLVING MASS AND WEIGHT
The mass of an object is the amount of matter it contains.
Example 1 :
If one egg has a mass of 55 g, find the total mass of eggs in 50 cartons, each containing 12 eggs.
Mass of 1 egg = 55 g
Number of eggs in each carton = 12
Total number of cartons = 50
Total mass = 55 x 12 x 50
= 33000 g
1000g = 1 kg
= 33 kg
Example 2 :
Find the total mass of 32 chocolates, each of mass 28 grams.
Number of chocolates = 32
Mass of each chocolate = 28 grams
Total mass = 32 x 28
= 896 grams
Example 3 :
If a clothes peg has a mass of 6.5 g, how many pegs are there in a 13 kg box?
Mass of 1 cloth peg = 6.5 g
Mass of box = 13 kg
1000 grams = 1 kg
Converting kg to grams, we get
= 13000 grams
Number of pegs = 13000/6.5
= 2000 pegs
Example 4 :
If a roof tile has mass 1.25 kilograms, how many tiles could a van with a load limit of 8 tonnes carry?
1000 kg = 1 tonne
8 tonnes = 8(1000)
= 8000 kg
Mass of 1 roof tile = 1.25 kg
Number of roof tiles carried by the van = 8000/1.25
= 6400 tiles
Example 5 :
Find the total mass in tonnes of 3500 books, each with mass 800 grams.
Mass of each book = 800 grams
Total number of books = 3500
Mass of 3500 books = 800 x 3500
= 2800000 grams
= 2800000/1000
= 2800 kg
1000 kg = 1 tonne
= 2800/1000
= 2.8 tonnes
Example 6 :
If the mass of 8000 oranges is 1.04 tonnes, what is the average mass of one orange?
Total number of oranges = 8000
Weight of oranges = 1.04 tonnes
= 1.04 (1000)
= 1040 kg
= 1040(1000)
= 1040000 grams
Average weight of 1 orange = 1040000 / 8000
= 130 grams
So, mass of 1 orange is 130 grams.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Derivative problems and solutions (part - 10).
Sep 27, 24 02:01 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Sep 26, 24 10:14 AM
Digital SAT Math Problems and Solutions (Part - 45)
Sep 26, 24 10:12 AM
The problem with new claims that Marlowe’s Doctor Faustus was co-written by a forgotten dramatist
Professor of Shakespeare Studies, De Montfort University
PhD Candidate, Languages and Literature, De Montfort University
Disclosure statement
The authors do not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and have disclosed no relevant affiliations beyond their academic appointment.
De Montfort University provides funding as a member of The Conversation UK.
View all partners

In Shakespeare’s time, about a quarter of all plays were collaboratively written by two or more dramatists. Christopher Marlowe’s classic work Doctor Faustus was first performed in the 1580s or early 1590s but only published in 1604, 11 years after his death. The dramatists Samuel Rowley and William Bird were paid in 1602 to write new additions to the play.
However, researchers have long suspected that the original play was not written by Marlowe alone. Its broader comic parts, largely in prose, have been thought to be the work of a second writer who never got the credit they deserved.
Previous research has suggested one of the dramatists Thomas Nashe or Henry Porter. Nashe left us only one play, Summer’s Last Will and Testament (1592). Porter wrote several in collaboration with other dramatists, but only one sole-authored play survives, The Two Angry Women of Abingdon (1599).
So, can a new computer analysis of texts resolve this question and finally credit the second author of Doctor Faustus?
In an article in the journal Notes & Queries and a piece in the Guardian , Darren Freebury-Jones describes computer techniques that point to Marlowe’s co-author being Porter. But we have found methodological problems in Freebury-Jones’s approach, and believe the evidence he presents does not support the conclusions he draws from it.
Computational analysis can certainly generate new knowledge about authorship, but his work is not a convincing example of this burgeoning art.
Unique matches
Freebury-Jones’s Notes & Queries article presents tables from a free online dataset, Collocations and N-Grams , created by independent Shakespeare analyst Pervez Rizvi. For 527 plays from the 1550s to the 1650s (pretty much all of those that have survived from this period), the dataset lists all four-word phrases that each play has in common with the other 526.
But the phrases Rizvi considers most significant are those that appear only in the play under consideration and one other play – known as “unique matches”. For each of the 527 plays, he ranks which other plays have the most unique matches to it.
If these rare phrases are particular to each dramatist’s idiolect (unique way of speaking), then researchers should, for example, find at the top of the Macbeth table some other plays by Shakespeare. And we do: among the top-ten plays that share the most unique matches with Macbeth are Julius Caesar, Coriolanus, King Lear and Hamlet.
But while the top-ten list for Macbeth gives grounds for optimism about Freebury-Jones’s method, since four of its plays are Shakespeare’s, the top-ten list for Doctor Faustus, reproduced below, dashes this:
- The Taming of a Shrew
- A Trick to Catch the Old One
- The Devil’s Charter
- Caesar and Pompey, or Caesar’s Revenge
- The Family of Love
- Messalina, the Roman Empress
- The Sisters
- The Two Angry Women of Abingdon
- Tamburlaine
While Porter is present in this list as the author of The Two Angry Women of Abingdon, Marlowe himself has only one play in it: Tamburlaine (1587) at position ten. If this method were detecting authorship, Marlowe’s other plays should dominate the list, just as the Macbeth list is dominated by Shakespeare plays.
Moreover, Porter’s play also appears at number ten for unique matches with Macbeth. This suggests the evidence for Porter being a coauthor of Macbeth is almost as strong as for Doctor Faustus – but Freebury-Jones makes no mention of this.
Porter can hardly be expected to dominate any top-ten list as Shakespeare does for Macbeth, since he left us only play. In contrast, with his roughly 1 million words of writing, Shakespeare presents a much greater “surface area” to any method that counts rare words or phrases – so he has more opportunities than anyone else to write the rare phrases we are looking for. To compensate for this, Rizvi discounts the significance of matches to authors with large canons.
Freebury-Jones mentions that the raw counts “are divided by the combined word counts for each pairing”, which is the scaling process Rizvi describes in the notes to Collocations and N-Grams. But nobody knows if this is the right way to scale for different canons or not, because the science of this problem has not been explored.
Rizvi changed his scaling formula in 2018 at my (Gabriel Egan’s) suggestion. But I did not claim to have solved the problem, and I consider it an open question whether we can derive a fair formula for such scaling.
Furthermore, Rizvi’s dataset does not distinguish between the plays that Shakespeare wrote alone and those he co-wrote, so his scaling factor treats as Shakespeare’s some substantial writings of other authors.
Further problems
This highlights another question with the analysis. In the top-ten list for unique matches with Macbeth are two plays co-authored by the dramatists Francis Beaumont and John Fletcher: The Woman Hater (1606) and Philaster (1620) .
So, what should a researcher do when a play has more than one author? One response is to count matches to Beaumont’s part separately from matches to Fletcher’s part, using the widely accepted divisions of these two plays – as first proposed by Cyrus Hoy , an expert in the English Renaissance stage, in 1958. Alternatively, you could exclude co-authored plays entirely, as many authorship investigators do.
But Freebury-Jones says nothing about this problem of judging writers by their co-authored works. This consideration bears somewhat on Macbeth too, since many Shakespearians believe the playwright Thomas Middleton wrote about 5%-10% of it.
So where does all this leave Porter? Freebury-Jones ends his Notes & Queries piece with a cautious claim: “We may reasonably conclude that Henry Porter is a likelier candidate than [Thomas] Nashe for Marlowe’s collaborator on Doctor Faustus.”
But in speaking to the Guardian, he abandoned this caution. He reports being “astonished by just how close the dramatic language of Doctor Faustus actually was to Porter”, and insists that we must recognise “Porter as the most likely collaborator”.
It’s possible that Porter did co-write Doctor Faustus. But the problems with Freebury-Jones’s analysis mean that, for now, we still can’t say for sure.

Looking for something good? Cut through the noise with a carefully curated selection of the latest releases, live events and exhibitions, straight to your inbox every fortnight, on Fridays. Sign up here .
- Shakespeare
- Christopher Marlowe
- Elizabethan theatre
- Renaissance
- Give me perspective

Economics Editor

Deputy Vice-Chancellor (Indigenous Strategy and Services)

Director and Chief of Staff, Indigenous Portfolio

Chief People & Culture Officer
Lecturer / senior lecturer in construction and project management.

IMAGES
VIDEO
COMMENTS
See also Gravitational force Weight - Problems and Solutions. 3. The mass of a box is 1 kg and acceleration due to gravity is 9.8 m/s 2. Find (a) weight (b) the horizontal component and the vertical component of the weight. Solution. Weight : w = m g = (1 kg)(9.8 m/s 2) = 9.8 kg m/s 2 = 9.8 Newton.
Practice mass and weight word problems in customary, metric or mixed units. No conversions of units are needed. Find more free math worksheets for kids in kindergarten to grade 5.
Learn the difference between mass and weight, and how they change with location and gravity. See examples, problems, and solutions on mass and weight conversion and force diagrams.
3. If the mass of a rock is 5 kg, what is its weight on Jupiter? 4. If the mass of an elephant is 5,678 kg on Earth, what is its mass on Venus? 5. If a book has a mass of 168 g, what is its weight on Earth? (You need mass in kg!) 6. If a dog has a mass of 12 kg, what is its weight on Neptune? 7. If a metal block has a mass of 22 kg, what is its ...
Weight of the object is W; Mass of the object is m; Acceleration due to gravity is g; Solved Examples. Numerical associated to weight calculations are provided underneath: Problem 1: Compute the weight of a body on the moon if the mass is 60Kg? g is given as 1.625 m/s 2. Answer: It is known that, m = 60 kg and. g = 1.625 m/s 2. Formula for ...
Practice mass and weight problems with customary and metric units. Solve addition, subtraction, multiplication or division of amounts with units of mass. No conversions between systems of units.
Weight is the force of gravity acting on an object due to its mass. The three things that affect gravity are location, location, location. ... Use the weight formula. W = mg. Solve for mass. Substitute one newton for weight and one standard earth gravity for gravity. m = W = 1 N: g: 9.8 m/s 2: m = 0.102 kg = 102 g: ... A problem for Americans ...
Express the answer clearly in a sentence or statement that answers the question posed in the word problem. Solving weight word problems requires a combination of mathematical skills, understanding of units of measurement, and critical thinking. Regular practice with a variety of problems can help students develop proficiency in solving such ...
A 1.0-kg mass thus has a weight of 9.8 N on Earth and only about 1.7 N on the Moon. The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body, such as Earth, the Moon, or the Sun. This is the most common and useful definition of weight in physics.
The total weight shown on the machine is 8 kg. If the weight of the plums is 2 kg 700 g, then what is the weight of the apples? 9. Jasmine purchased 7 kg 302 g of rice and Melissa purchased 3 kg 598 g more. What quantity of rice did Jasmine and Melissa purchase? 10. The weight of a chocolate carton is 20 kg. Each carton has 10 packets.
Solve problems involving density and specific gravity of rocks and minerals using formulas and examples. Test your knowledge with a quiz or download the questions as a PDF.
Each interactive concept-builder presents learners with carefully crafted questions that target various aspects of a discrete concept. There are typically multiple levels of difficulty and an effort to track learner progress at each level. Question-specific help is provided for the struggling learner; such help consists of short explanations of how to approach the situation.
Compare, describe and solve practical problems for mass/weight teaching resources for 2014 National Curriculum Resources. Created for teachers, by teachers! Professional Measurement teaching resources.
Solving problems with two unknowns. Explain how you know you have found all the possible solutions to a problem with two unknowns. Downloads. Download. Select resources to download. Lesson resources. Select all. Slide deck. PPTX. Worksheet. PDF. Worksheet. PPTX. Starter quiz questions. PDF.
Practice adding, subtracting, multiplying or dividing amounts with units of mass (lbs, kg, oz, g) in these worksheets. No conversion of units is required.
Key Points: The weight of an object tells us how heavy it is. 1 ounce is almost as light as a slice of bread. Key Points: The weight of an object tells us how heavy it is. ... Volume Word Problems. Teachers: Assign to students. Duplicate. Edit Questions. Edit Article. Assign. Preview Questions. Edit. Duplicate. Class Ace. Tech-Enhanced Learning.
Mass & weight word problems (customary units) Grade 4 Word Problems Worksheet 1. A bag of flour weigh 3 lbs. If a chef needs 15 lbs of flour, how ... The total weight of the roasted turkey is 20 lbs. 5. 2 lbs 4 oz = 2 x 16 oz + 4 oz = 36 oz 20 oz < 36 oz The box of butter weighs heavier. 6. 0.5 lbs = 8 oz
How to solve Weighted Averages and Mixture Problems? Mixture problems are problems in which two or more parts are combined into a whole. Examples: Premium coffee is $9.50/lb, Supreme coffee is $11.75/lb and Blend coffee is $10.00/lb. How many pounds of Premium coffee beans should be mixed with two pounds of Supreme coffee to make Blend coffee?
These are our mass and weight Word Problems worksheets for 2nd grade math school. Click on the previews to go to download page. Mass Problems (level 2) Mass Problems (level 2) Mass Problems (level 2) Worksheet by math grade levels: Grade 1 sheets. Grade 2 sheets. Grade 3 sheets.
Learn how to solve word problems involving mass and weight using simple examples and formulas. Find the mass of objects in different units and the average mass of a group of objects.
But nobody knows if this is the right way to scale for different canons or not, because the science of this problem has not been explored. Rizvi changed his scaling formula in 2018 at my (Gabriel ...