centre of mass experiment method

August 11, 2016

"X" Marks the Spot: Finding the Center of Mass

A centering science activity

By Ben Finio & Science Buddies

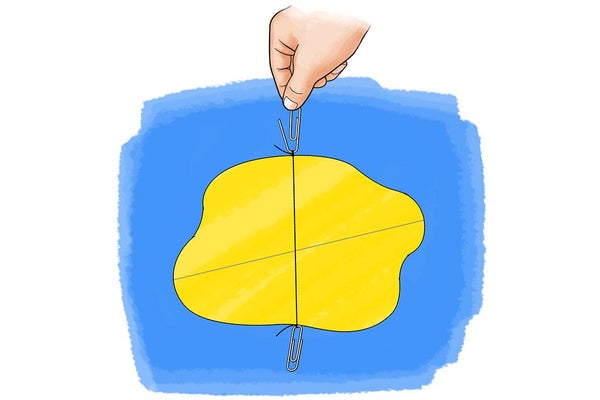
Can you find the center of a shape? You'll be able to--even for the oddest oblong creation--with this simple science activity. No strings attached (okay, maybe one)! 

George Retseck

Key concepts Physics Geometry Gravity Center of mass

Introduction With a little time, you can probably find the center of simple shapes such as circles and squares pretty easily. But how do you find the “middle” of an irregular shape such as a drawing of a dog or a cat? This project will show you how to do it using nothing but string and paper clips!

Background How do you define the exact center of an object? One way to do this is to find the object's center of mass. The center of mass is the point about which an object will balance if you try to rest it on your fingertip. Or if you hang an object, for example a picture frame from a nail, the center of mass will hang directly below the nail.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For symmetrical objects, finding the center of mass is relatively easy. For example, for a rectangular picture frame, you know the center of mass is in the middle of the rectangle and you can find that with a ruler. When you hang the picture frame, you will make sure it is centered on the nail—otherwise it will tip to one side and will be off-center. The same applies to other symmetrical objects such as a spherical basketball; you know the center of mass is in the middle of the sphere.

What about irregularly shaped objects such as a dog or cat or person? Now finding the center of mass is not so easy! This activity will show you how to find the center of mass for any two-dimensional shape you cut out of paper using a trick that has to do with the hanging picture frame mentioned above. If you hang a shape from a single point, you know the center of mass will always rest directly below that point. So, if you hang a shape from two different points (one at a time) and draw a line straight down from each point, the center of mass is where those lines intersect. This technique can be used for any irregular two-dimensional shape. Don't believe it? Try this activity to find out!

Paper (Heavier paper, such as construction paper, card stock or thin cardboard from the side of a cereal box will work best.)

Scissors (Have an adult help with cutting if necessary—especially on thicker materials.)

Two paper clips or a pushpin and another small, relatively heavy object you can tie to the string (such as a metal washer)

Preparation

Cut a piece of string about one foot long and tie a paper clip to each end. (Alternatively, you can use any other small object such as a metal washer on one end—this will serve as a weight—and any other small, pointy object like a needle or pushpin on the other end—this will be used to puncture the paper.)

Start with an easy shape: Cut out a rectangular piece of paper or cardboard. Can you guess where the center of mass of the rectangle is? If so, use a ruler to measure where you think it will be and mark this spot with your pencil.

Punch several small holes around the edge of the paper. Make them as close to the edge as possible without ripping the paper. (This is important for the accuracy of this technique). The exact location of the holes does not matter but this technique will work best if you space them all the way around the edge (not just put two holes right next to each other).

Now poke one end of one paper clip (or pushpin) through one of the holes to act like a hanging hook. Make sure the paper can swing easily from the hook and does not get stuck (Rotate it back and forth a few times to loosen the hole if necessary).

Hold on to your “hook” and hold the paper up against the wall. Let the paper swing freely and make sure the string can hang straight down and does not get stuck.

Use a pencil and ruler to draw a straight line on the paper along the string. Does this line go through the center of mass you predicted earlier?

Now, hang your paper from a different hole and repeat the process. Where does this line intersect the first line?

Repeat the process several more times with different holes. Do all the lines intersect at the same point?

Now cut out an irregular shape. You can cut out a “blob” or draw something like a dog or cat and then cut out the outline. Make sure the shape you cut out remains stiff and flat. (That is, do not cut very thin sections that might be floppy.) Can you use a ruler to predict where the center of mass of your irregular shape will be? This is much harder!

Punch holes around the edge of your irregular shape and repeat the activity. One at a time, hang the shape and the string from one of the holes and draw a line along the string. Where do the lines intersect? Does this match up with what you predicted?

Extra: If you use a stiff enough material to cut out your shape (such as cardboard), can you try balancing it on your fingertip at the center of mass? What happens if you try to balance it about another point?

Observations and results You should have found that the center of mass of the rectangle is right in the middle of the piece—halfway along the width and halfway along the height. You can easily locate this spot with a ruler. Then, when you hang the rectangle from a hole on its edge, the string should always pass through this point, regardless of which hole you use. Whereas it is much harder to predict the center of mass for an irregular shape, the same principle holds true. Regardless of what point you hang the irregular shape from, the string will always pass through the center of mass. So, if you hang it from two or more points (one at a time), you can find the intersection of these lines—and that is the center of mass.

Note that due to small variables in the activity (such as friction on the hook that prevents the paper from rotating perfectly or the holes not being close enough to the edge of the paper), if you draw multiple lines, they might not all intersect in exactly the same place but they should still be fairly close to one another.

More to explore Fun with Gravity and Center of Mass ( pdf ), from Gravity Recovery and Climate Experiment Circus Science: How to Balance Anything , from Scientific American Swinging with a Pendulum , from Scientific American Science Activities for All Ages! from Science Buddies

This activity brought to you in partnership with Science Buddies

Sciencing_Icons_Science SCIENCE

Sciencing_icons_biology biology, sciencing_icons_cells cells, sciencing_icons_molecular molecular, sciencing_icons_microorganisms microorganisms, sciencing_icons_genetics genetics, sciencing_icons_human body human body, sciencing_icons_ecology ecology, sciencing_icons_chemistry chemistry, sciencing_icons_atomic & molecular structure atomic & molecular structure, sciencing_icons_bonds bonds, sciencing_icons_reactions reactions, sciencing_icons_stoichiometry stoichiometry, sciencing_icons_solutions solutions, sciencing_icons_acids & bases acids & bases, sciencing_icons_thermodynamics thermodynamics, sciencing_icons_organic chemistry organic chemistry, sciencing_icons_physics physics, sciencing_icons_fundamentals-physics fundamentals, sciencing_icons_electronics electronics, sciencing_icons_waves waves, sciencing_icons_energy energy, sciencing_icons_fluid fluid, sciencing_icons_astronomy astronomy, sciencing_icons_geology geology, sciencing_icons_fundamentals-geology fundamentals, sciencing_icons_minerals & rocks minerals & rocks, sciencing_icons_earth scructure earth structure, sciencing_icons_fossils fossils, sciencing_icons_natural disasters natural disasters, sciencing_icons_nature nature, sciencing_icons_ecosystems ecosystems, sciencing_icons_environment environment, sciencing_icons_insects insects, sciencing_icons_plants & mushrooms plants & mushrooms, sciencing_icons_animals animals, sciencing_icons_math math, sciencing_icons_arithmetic arithmetic, sciencing_icons_addition & subtraction addition & subtraction, sciencing_icons_multiplication & division multiplication & division, sciencing_icons_decimals decimals, sciencing_icons_fractions fractions, sciencing_icons_conversions conversions, sciencing_icons_algebra algebra, sciencing_icons_working with units working with units, sciencing_icons_equations & expressions equations & expressions, sciencing_icons_ratios & proportions ratios & proportions, sciencing_icons_inequalities inequalities, sciencing_icons_exponents & logarithms exponents & logarithms, sciencing_icons_factorization factorization, sciencing_icons_functions functions, sciencing_icons_linear equations linear equations, sciencing_icons_graphs graphs, sciencing_icons_quadratics quadratics, sciencing_icons_polynomials polynomials, sciencing_icons_geometry geometry, sciencing_icons_fundamentals-geometry fundamentals, sciencing_icons_cartesian cartesian, sciencing_icons_circles circles, sciencing_icons_solids solids, sciencing_icons_trigonometry trigonometry, sciencing_icons_probability-statistics probability & statistics, sciencing_icons_mean-median-mode mean/median/mode, sciencing_icons_independent-dependent variables independent/dependent variables, sciencing_icons_deviation deviation, sciencing_icons_correlation correlation, sciencing_icons_sampling sampling, sciencing_icons_distributions distributions, sciencing_icons_probability probability, sciencing_icons_calculus calculus, sciencing_icons_differentiation-integration differentiation/integration, sciencing_icons_application application, sciencing_icons_projects projects, sciencing_icons_news news.

• Share Tweet Email Print
• Home ⋅

Center of Mass: Definition, Equation, How to Find (w/ Examples)

Have you ever seen one of those toy birds that is able to balance on your fingertip by its beak without tipping over, as if by magic? It isn’t magic that allows the bird to balance at all, but the simple physics associated with center of mass.

Understanding the physics behind the center of mass allows you not only to understand conservation of momentum and other related physics, but can also inform stability and dynamics in the sports you play, as well as allow you to perform some creative balancing acts.

Definition of Center of Mass

An object’s ​ center of mass ​, sometimes also called the center of gravity, can be thought of as the point where the total mass of an object or a system can be treated as a point mass. In certain situations, external forces can be treated as though they are acting on the center of mass of the object.

For the toy bird balancing on your fingertip, the center of mass is at its beak. This might seem wrong at first, which is why the act of balancing appears magical. Indeed, for a bird sitting on a branch, its center of mass is somewhere in its body. But the balancing bird toy often has weighted wings that span outward and forward, causing it to balance differently.

The center of mass can be determined for a single object – such as the balancing bird – or it can be computed for a system of several objects, as you will see in a later section.

Center of Mass for a Single Object

There will always be a single point on a rigid body that is the location of that body’s center of mass. The position of the center of mass of an object depends on the distribution of mass.

If an object is of uniform density, its center of mass is easier to determine. For example, in a circle of uniform density, the center of mass is the center of the circle. (This would not be the case, however, if the circle was denser on one side than the other).

In fact, the center of mass will always be at the geometric center of the object when density is uniform. (This geometric center is called the ​ centroid ​.)

If the density is not uniform, there are other ways to determine the center of mass. Some of these methods involve the use of calculus, which is beyond the scope of this article. But one simple way to determine the center of mass of a rigid object is to simply try to balance it on your fingertip. The center of mass will be at the balancing point.

Another method, useful for planar objects, is as follows:

• Suspend the shape from one edge point along with a plumb line.
• Draw a line on the shape that lines up with the plumb line.
• Suspend the shape from a different edge point along with a plumb line.
• Draw a line on the shape that lines up with the new plumb line.
• The two lines drawn should intersect at a single point.
• This unique intersection point is the location of the center of mass.

For some objects, however, it is possible for the balance point to be outside the bounds of the object itself. Think of a ring, for example. The center of mass for a ring shape is in the center, where no part of the ring exists at all.

Center of Mass of a System of Particles

The position of the center of mass for a system of particles can be thought of as their average mass position.

The same idea can be used as for a rigid object if you imagine this system of particles are all connected by rigid, massless plane. The center of mass would then be the balance point of that system.

To determine the center of mass of a system of particles mathematically, the following simple formula can be used:

Where ​ M ​ is the total mass of the system, ​ m i ​ are the individual masses and ​ r i ​ are their position vectors.

In one dimension (for masses distributed along a straight line) you can replace ​ r ​ with ​ x ​.

In two dimensions, you can find the ​ x ​-coordinate and ​ y ​-coordinate of the center of mass separately as:

Examples of Calculating the Center of Mass

​ Example 1: ​ Find the coordinates of the center of mass of the following system of particles: particle of mass 0.1 kg located at (1, 2), particle of mass 0.05 kg located at (2, 4) and particle of mass 0.075 kg located at (2, 1).

​ Solution 1: ​ Apply the formula for the ​ x ​-coordinate of the center of mass as follows:

Then apply the formula for the ​ y ​-coordinate of the center of mass as follows:

So the location of the center of mass is (0.079, 2.11).

​ Example 2: ​ Find the location of the center of mass of a uniform density equilateral triangle whose vertices lie at points (0, 0), (1, 0) and (1/2, √3/2).

​ Solution 2: ​ You need to find the geometric center of this equilateral triangle with side length 1. The ​ x ​-coordinate of the geometric center is straightforward – it is simply 1/2.

The ​ y ​-coordinate is a little trickier. It will occur at the location that a line from the top of the triangle to the point (0, 1/2) intersects with a line from any of the other vertices to the midpoint of one of the opposite side. If you sketch such an arrangement, you will find yourself with a 30-60-90 right triangle whose long leg is 0.5 and short leg is the ​ y ​-coordinate. The relationship between these sides is √3y = 1/2, hence y = √3/6, and the coordinates of the center of mass are (1/2, √3/6).

Motion of the Center of Mass

The location of the center of mass of an object or system of objects can be used as a reference point in many physics calculations.

When working with a system of interacting particles, for example, finding the center of mass of the system allows for an understanding of linear momentum. When linear momentum is conserved, the center of mass of the system will move with a constant velocity even as the objects themselves bounce off one another.

For a falling rigid object, gravity can be treated as acting on that object’s center of mass, even if that object is rotating.

The same is true of projectiles. Imagine tossing a hammer, and as it flies through an arc in the air, it rotates end over end. This might seem like complex motion to model at first, but it turns out that the center of mass of the hammer moves in a nice smooth parabolic path.

A simple experiment can be performed which demonstrates this by taping a small piece of glow tape to the hammer’s center of mass, and then tossing the hammer as described in a dark room. The glow tape will appear to move in a smooth arc, like a tossed ball.

A Simple Experiment: Find the Center of Mass of a Broom

A fun center-of-mass experiment that you can perform at home involves using a simple technique for finding the center of mass of a broom. All you need for this experiment is one broom and two hands.

With your hands relatively far apart, hold up the broom on the end of two pointer fingers. Then, slowly bring your hands closer together, sliding them underneath the broom. As you move your hands closer together you may notice one hand wants to slide along the underside of the broom handle while the other one stays put for a while before sliding.

The entire time your hands move, the broom remains balanced. Eventually, when your two hands meet, they will meet at the location of the broom’s center of mass.

Center of Mass of the Human Body

The center of mass of the human body is located somewhere near the navel (belly button). In men, the center of mass tends to be a little higher since they carry more body mass in their upper body, and in women, the center of mass is lower because they carry more mass in their hips.

If you stand on one foot, your center of mass will shift toward the side of the foot you are standing on. You may notice yourself leaning more toward that side. This is because in order to stay balanced, your center of mass needs to stay over the foot you are balancing on, or else you will tip over.

If you stand with one leg and hip against a wall and try to lift your other leg, you will likely find it impossible because the wall prevents your weight from shifting over the balance leg.

Another thing to try is standing with your back to the wall and your heels touching the wall. Then try to bend forward and touch the floor without bending your legs. Women may be more successful at this task than men because their center of mass is lower in their body and may end up still being over their toes as they lean forward.

Center of Mass and Stability

The location of the center of mass relative to an object’s base determines its stability. Something is considered stably balanced if, when tipped slightly and then released, it then returns back to its original position instead of tipping further and falling over.

Consider a three-dimensional pyramid shape. If balanced on its base, it is stable. If you lift one end slightly and let it go, it falls back down. But if you try to balance the pyramid on its tip, then any deviations from perfect balance will cause it to fall over.

You can determine if an object will fall back to its original position or tip over by looking at the location of the center of mass relative to the base. Once the center of mass moves past the base, the object will tip over.

If you play sports, you might be familiar with the ready position where you stand with a wide stance and knees bent. This keeps your center of mass low, and the wide base makes you more stable. Consider how hard someone would have to push you to tip you over if you are in the ready position vs. when you are standing up straight with your feet together.

Some cars have problems with rolling over when they take sharp turns. This is because of the location of their center of mass. If the center of mass of a vehicle is too high and the base is not wide enough, then it doesn’t take much to cause it to tip over. It’s always best for the stability of a vehicle to have most of the weight as low as possible.

Related Articles

Science project on how the mass of a paper airplane..., what are the three principles of gravity that affect..., levers used in everyday life, how to build a knee school project, how to use a single and double pulley system, principles of pulleys & levers, how to calculate cg, how to calculate center of mass, how to make a model of the pivot joint, how to make a clay model of the urinary system, how to make a compass at home for geometry, tips to make a strong marshmallow tower, how to make a bridge out of straws, how to find a hermit crab, how to build a model of the leaning tower of pisa, how to build a catenary curve arch, how to build an easy catapult for kids, 6 types of freely movable joints.

• Georgia State University HyperPhysics: Center of Mass
• Top End Sports: Center of Gravity

About the Author

Gayle Towell is a freelance writer and editor living in Oregon. She earned masters degrees in both mathematics and physics from the University of Oregon after completing a double major at Smith College, and has spent over a decade teaching these subjects to college students. Also a prolific writer of fiction, and founder of Microfiction Monday Magazine, you can learn more about Gayle at gtowell.com.

Find Your Next Great Science Fair Project! GO

• Sign in / Register
• Administration
• My Bookmarks
• My Contributions
• Activity Review
• Edit profile

The PhET website does not support your browser. We recommend using the latest version of Chrome, Firefox, Safari, or Edge.

Centre of Mass

In this article we are going to learn about centre of mass, performing and describing an experiment to determine the position of the centre of mass of a plane lamina. describe qualitatively the effect of the position of the centre of mass on the stability of simple objects., definition of terms:.

Centre of mass or centre of gravity : is a point at which the mass of a body seems to be concentrated at and the body’s weight can be considered to act at this point even though the Earth attracts every part of it.

Centre of mass of a plane lamina:

Experiment to find centre of mass of a plane lamina

Materials : lamina (irregular paper), nail, thread, weight (object), stand, ruler and pencil.

Step 1 : Make a hole A in the lamina.

Step 2 : Hang lamina so that it can swing freely on a nail clamped in a stand and wait for it to be at rest.

Step 3 : Tie a plumb line (a thread and a weight) to the nail.

Step 4 : Draw a straight line along thread using a ruler and mark line (plumb line) A and B with a pencil.

Step 5 : Repeat step 1, 2, 3 and 4 at a different point and mark line C and D with a pencil.

Step 6 : Make a point where two lines intersect. This point is the centre of mass of a plane lamina.

Stability and three States of equilibrium:

1. Stable equilibrium : A body is in stable equilibrium if when slightly displaced and then released it returns to its previous position.

2. Unstable equilibrium : A body is in unstable equilibrium if it moves further away from its previous position when slightly displaced and released.

3. Neutral equilibrium : A body is in neutral equilibrium if it stays in its new position when displaced. Its centre of mass does not rise or fall because there is no moment to increase or decrease the displacement.

Ways to increase stability of a body:

(a) Lowering its centre of mass.

(b) Increasing the area of its base.

In this article we learnt about centre of mass, performing and describing an experiment to determine the position of the centre of mass of a plane lamina. describe qualitatively the effect of the position of the centre of mass on the stability of simple objects.

Terms of service.

Terms and Conditions ("Terms")

Last updated: (10 th June 2023)

Please read these Terms and Conditions ("Terms", "Terms and Conditions") carefully before using the http://www.scienceinlesotho.com website (the "Service") operated by scienceinlesotho ("us", "we", or "our").

Your access to and use of the Service is conditioned on your acceptance of and compliance with these Terms. These Terms apply to all visitors, users and others who access or use the Service.

By accessing or using the Service you agree to be bound by these Terms. If you disagree with any part of the terms then you may not access the Service.

You are free to study with us and all courses offered are paid with time limit, and any course may be blocked automatically if time limit is reached.

If you wish to purchase any product or service made available through the Service ("Purchase"), you may be asked to supply certain information relevant to your Purchase including, without limitation personal details, and payments are made online (on this website) or offline and payments are non-refundable.

Our Service allows you to comment, contact, link, store, share and otherwise make available certain information, text, graphics, videos, or other material ("Content"). You are responsible for the charges of any calls you make.

The Content and products as well as prices are provided by scienceinlesotho and all content is public to all users but you can hide your profile at any time.

Links To Other Web Sites

Our Service may contain links to third-party web sites or services that are not owned or controlled by scienceinlesotho.

We scienceinlesotho has no control over, and assumes no responsibility for, the content, privacy policies, or practices of any third party web sites or services. You further acknowledge and agree that scienceinlesotho shall not be responsible or liable, directly or indirectly, for any damage or loss caused or alleged to be caused by or in connection with use of or reliance on any such content, goods or services available on or through any such web sites or services.

We reserve the right, at our sole discretion, to modify or replace these Terms at any time. If a revision is material we will try to provide at least 30 days' notice prior to any new terms taking effect. What constitutes a material change will be determined at our sole discretion.

If you have any questions about these Terms, please contact us.

Terms of Use

Privacy policy, frequently asked questions.

We offer both physical and online classes.

How to be scienceinlesotho student?

1. You need to contact us via WhatsApp, call, mail, email, Facebook or website .

2. We will add you to our WhatsApp group, then after you have paid your monthly fee for any supported course you like to study; We register you to Learning Management System ( portal ) to access online courses ( classes ) and teachers.

3. All physical learning students will access online courses ( classes ) and teachers for official announcements, tests, asking teachers questions and many more.

How to Access classes?

Answer: Just click clsses tab on the menu or click take courses or portal link and will be directed to courses or portal page.

How to enrol or take course?

Answer: Please bear in mind that you should contact admins then you will be able to buy and enrol into a course.

How to pay courses?

Answer: You have two options.

You can pay via Mpesa or Ecocash.

Will provide bank account soon.

How do I contact admins?

Answer: You are free to contact us on all provided methods of contacting us like whatsApp, facebook, calls, mails and many more. .