problem solving with long division

WELCOME!     Find what you need

Elementary Math

Elementary Ela-Reading

Teaching Tips

Career Exploration

How to solve long division problems.

Refresh your memory on how to teach long division with success for students and yourself. This step-by-step guide is filled with tips and helpful advice.

So many teachers become frustrated while teaching students how to solve long-division problems. I know that feeling well; I’ve been there. But teaching long division doesn’t have to be as difficult as that – cross my heart! 

I’ll walk you through a few steps that make long division easier for you to teach. But first, let’s talk to our students about what long division is and why it exists in the first place.

Introduce the topic to students.

As you’re introducing long division to students, setting the right tone is important. They shouldn’t be told how hard it is or that it’s scary and tough to learn. They need reassurance and confidence that they’ll be successful with your help.

Say something like, “I know you’re excited to learn about long division. We’ll use many skills you’ve learned over the years and put them together to solve division problems.”

Go on to explain that long division is simply a way of splitting a number into smaller, even parts. In real-life terms, it’s a way of dividing a big group of things into many smaller groups. 

For example, if we have a bag of candies and a group of children. We want each child to get the same number of candies, so we need to figure out how many candies each child gets. We can find the answer through long division.

Teach the basic terminology.

While instructing students, you should use the correct terminology. Here’s a quick refresher:

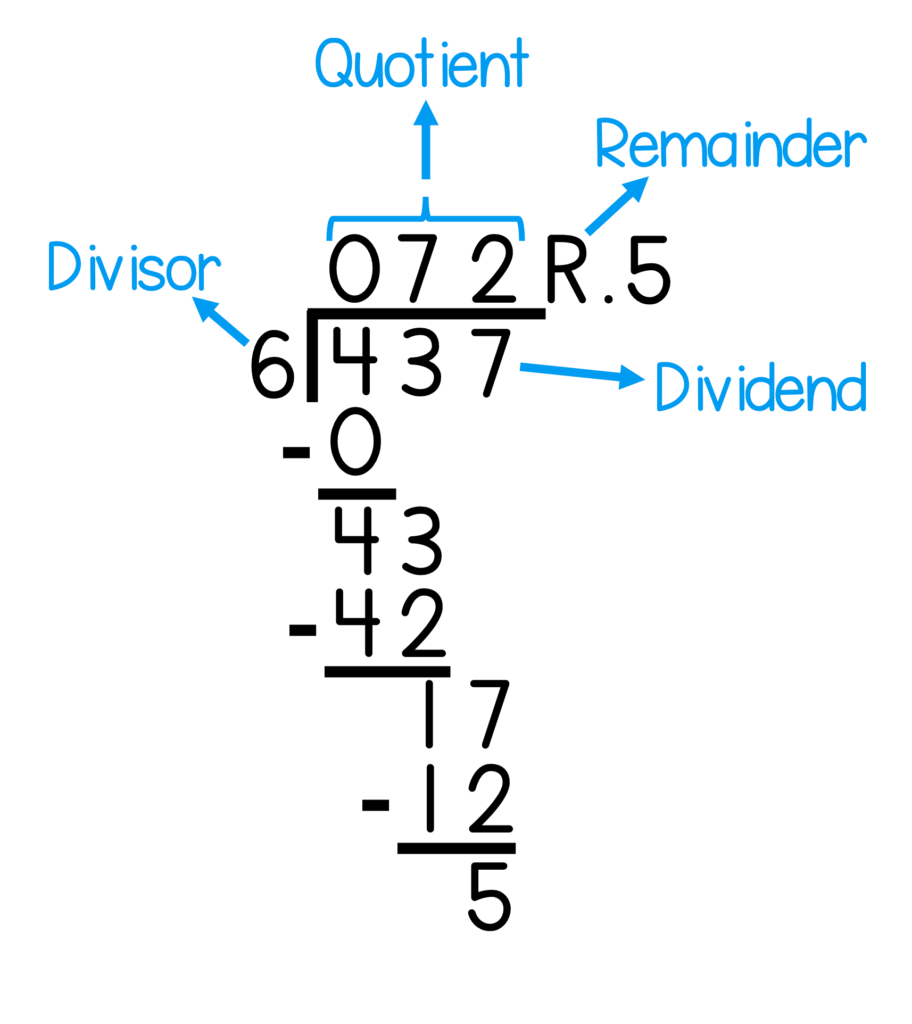
• The dividend is the number being divided or split up (the number inside the division symbol).
• The divisor is the number you divide by (the number of groups the dividend is split into).
• The quotient is the name of the answer to the division problem (how many are in each group).
• The remainder is the number that is left over after dividing.

In other words, dividend ÷ divisor = quotient , and the remainder is any extra amount.

You may have to provide several more examples to help students understand why we perform long division.

Long division can be broken down into steps.

Long division is a process that can be broken down into steps. Teaching each step will make it easier for students to become fluent. Long division takes practice, repetition, and feedback, but students will master the skill over time.

As you begin to instruct students on the steps for solving long division, follow these steps:

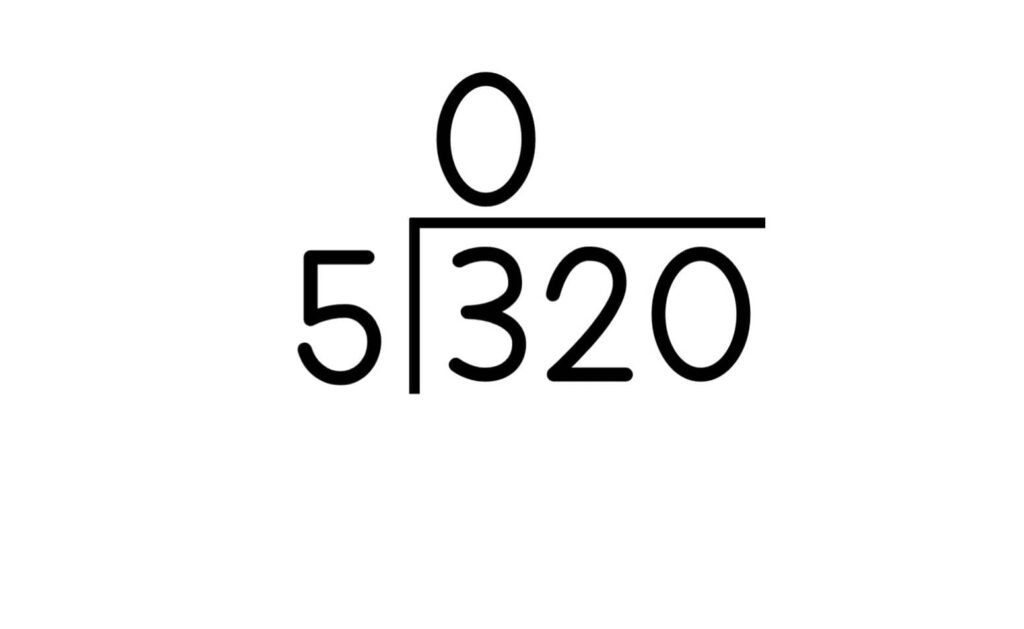
1. Set up the equation with a dividend and divisor. 

2. Divide the first digit in the dividend by the divisor by finding how many times the divisor can go into the first digit of the dividend. Write that number above the first digit of the dividend. That is the first digit of the quotient. In the above example, ask how many groups of 5 are there in 3?

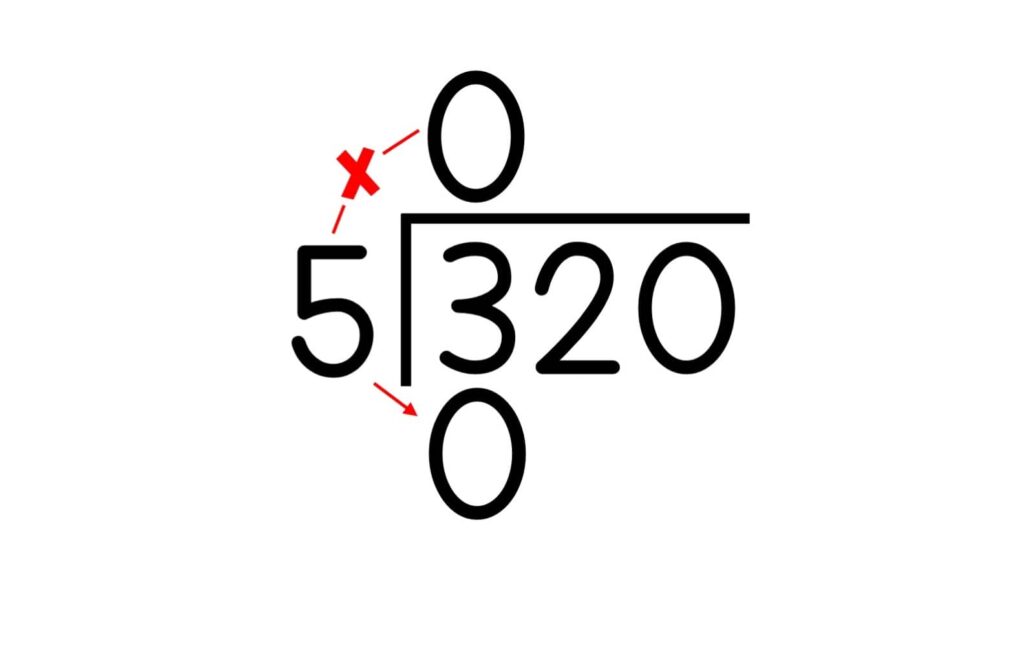
3. If the divisor is larger than the first digit, place a zero above the first digit of the dividend

4. Multiply the digit in the quotient times the divisor. In our example, this is 0.

5. Write the product below the dividend.

6. Write a line under the product.

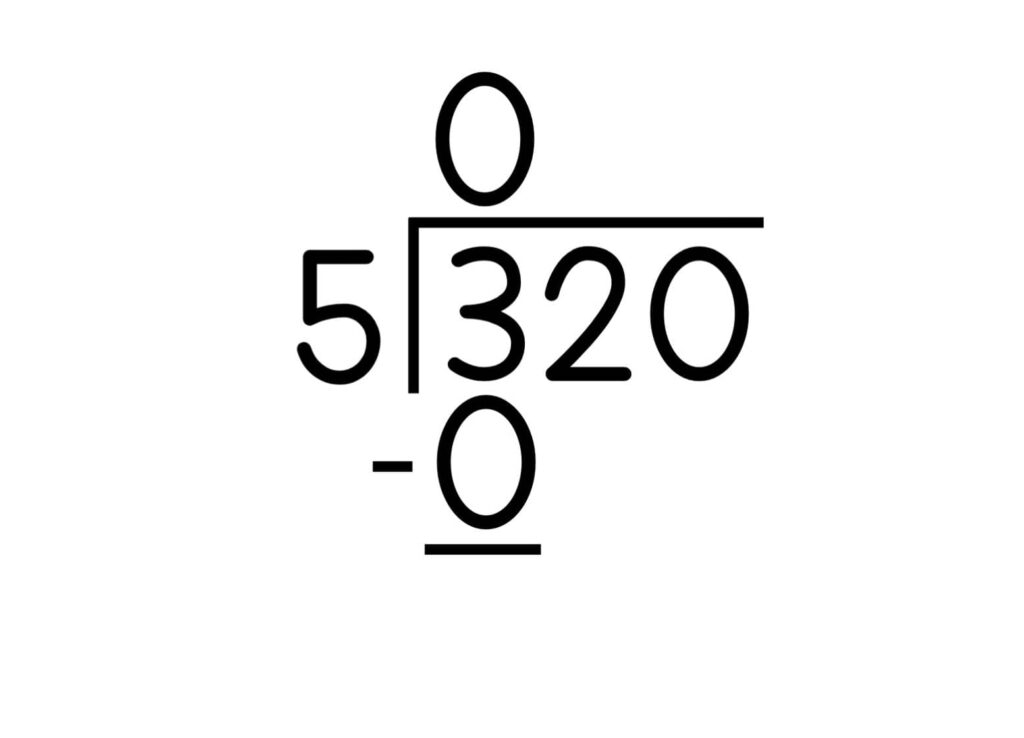
7. Subtract the product from the dividend. Write the difference (answer) under the line.

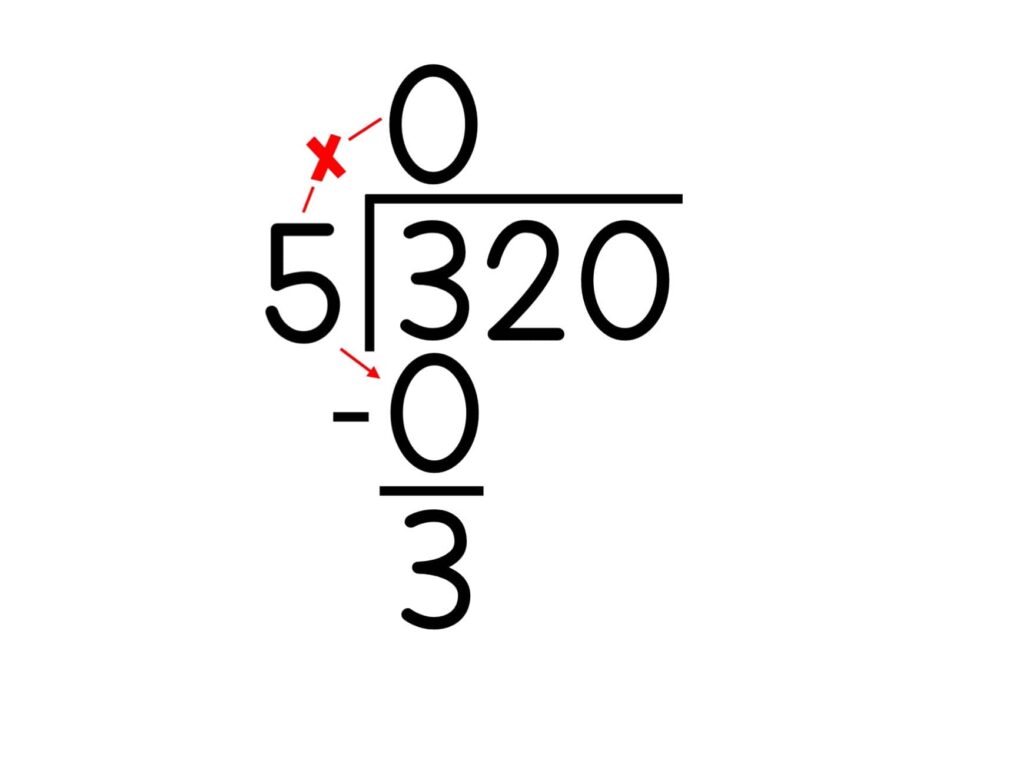
8. Bring down the next digit in the dividend.

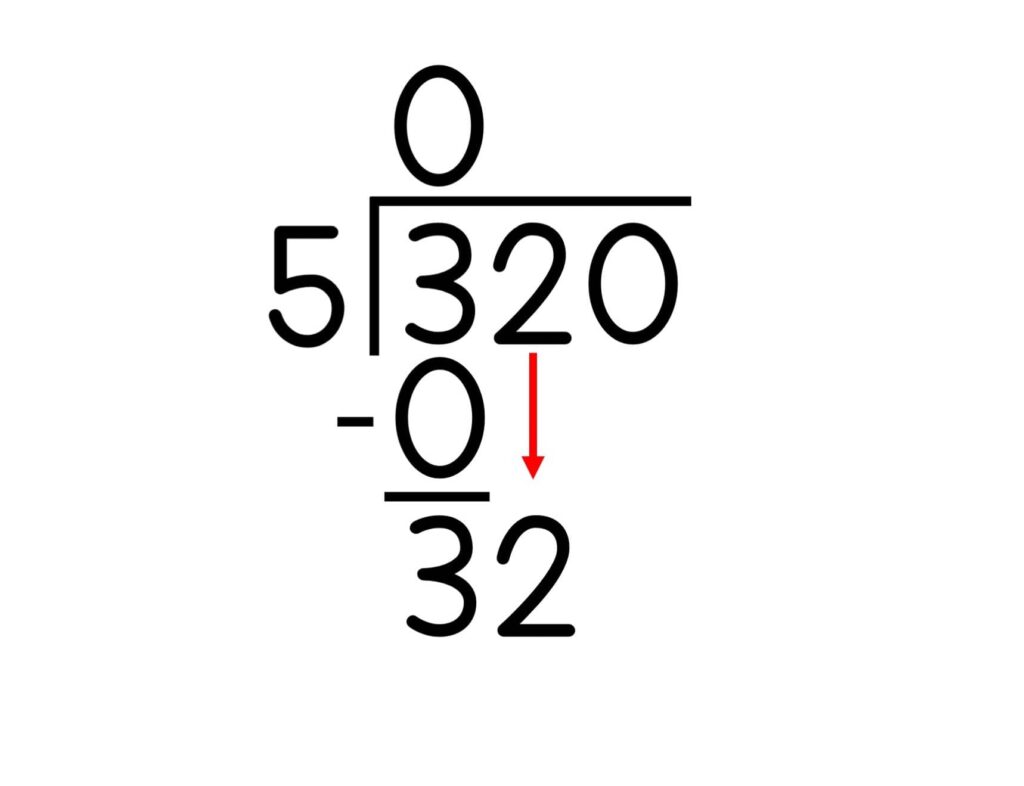
9. Repeat the process by dividing the new number by your divisor. Write that digit above the dividend as the next digit of the quotient. Continue this process until all the digits in the dividend have been brought down and divided.

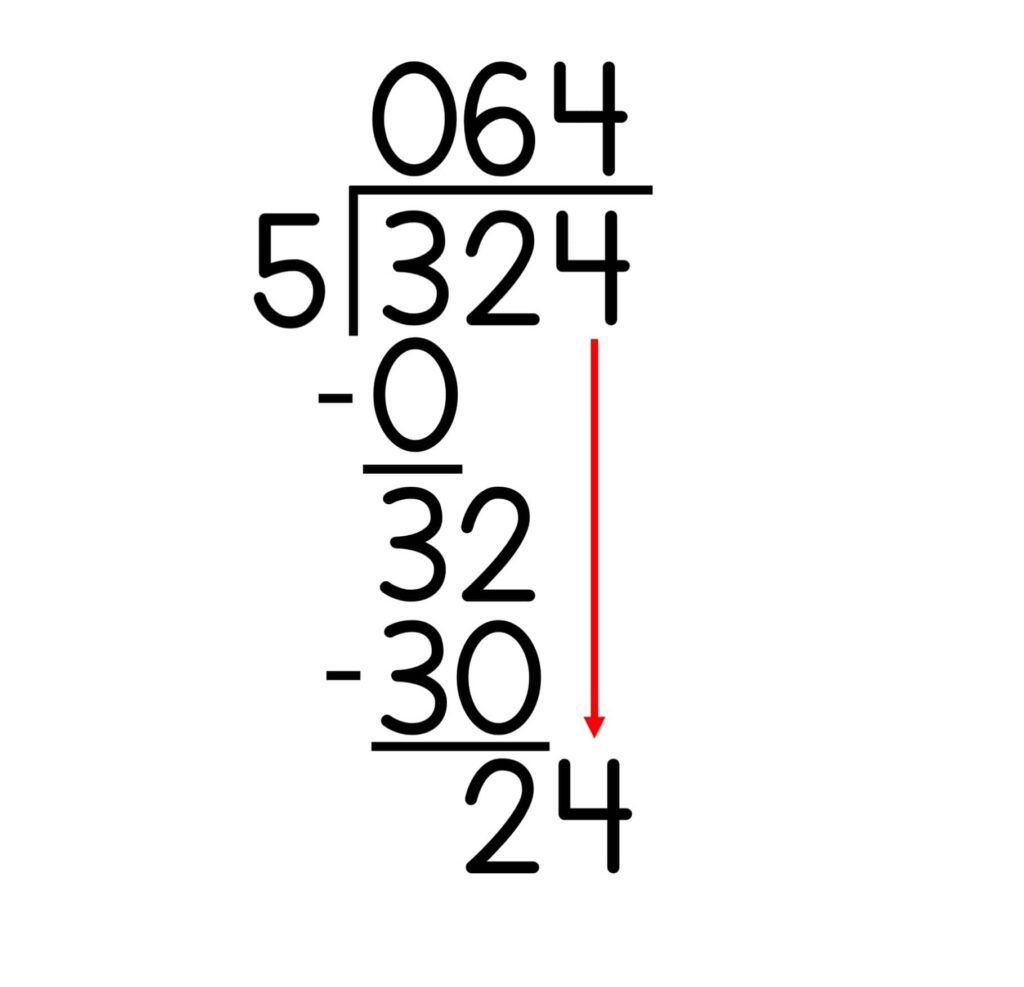
10. If the numbers don’t divide evenly, you’ll be left with a remainder. After the quotient, write “R.” and then the number left over. In our example, that remainder is 4.

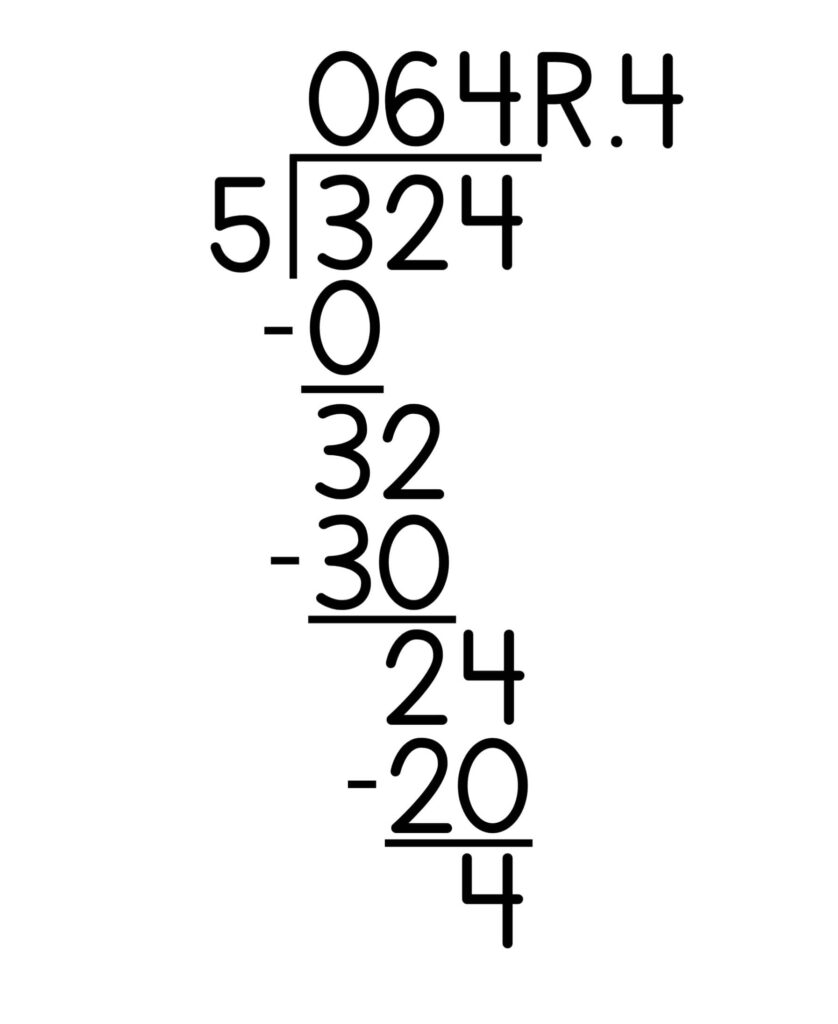
11. Remember to label your quotient and final answer. If you divide candies between children, you’ll label the final answer “candies.”

Provide several examples and think out loud.

Students learn a lot by hearing how you problem solve. 

As you’re explaining the examples, be sure to model your thinking out loud. For example, you might say, “Hmm. How many groups of 7 can be taken out of 30? I know 7 x 4 is 28, and that’s pretty close to 30.”

Be sure to:

• Over-teach by providing plenty of examples.
• Explain your thinking and reasoning for each step of the process.
• Be consistent. Repeat the process the same way every time.
• Provide real-world examples to help students understand how we use division in real-life situations.
• Use visual aids such as anchor charts, reference guides, posters, and diagrams to illustrate the concepts.
• Provide frequent feedback. The more often you provide feedback, the more students can self-correct.

Practice, practice, practice in a group.

Provide a long division problem for students to solve at their seats using whiteboards or paper. Have students practice problems independently or with assistance from a partner. As students are working, circulate around the room to provide frequent feedback. Once most students are finished, invite a student to show their work as they solve the problem in front of the class. Sometimes hearing the steps from a peer helps students understand. Discuss problem areas before moving on to the next problem.

As you’re circulating around the room, if you see students having trouble, ask them questions about their thinking processes. Make corrections on the spot to ensure that students understand the steps. 

You can also have students use their whiteboards for questions about what they don’t understand. 

More about partner work.

Partner work with whiteboards is a great way for students to learn from each other. They can also check each other’s work while practicing to improve their skills. Teaching others is the highest form of understanding, so students who are comfortable with the process can help classmates who are still struggling. Both students benefit. 

Important note – Peer tutoring can be a valuable part of learning for both students. However, don’t overuse it. Advanced students should be challenged so they continue moving forward. Struggling students need direct instruction from trained teachers. Use this approach wisely.

During partner work, you can circulate around the room and catch students’ mistakes immediately. The immediate feedback and reinforcement save students time and frustration. 

Be sure to note the students who need more assistance. You can work with those individuals in a small group or individually.

My favorite method for teaching long division.

My absolute favorite method for teaching long division is Shaped Math . It’s fantastic for introducing long division and for students who need support. 

Check out the video that explains this visual support for teaching long division.

Grab This FREE Long Division Set:

Grab the FREE Shaped Math Long Division.

Learn more about How to Teach Long Division with Shaped Math.

Additional tools to support students:

For students who need additional support, try out graph paper accommodations.

Standard Algorithm Using Shaped Math.

Conclusion .

Hopefully, you’ve found these tips helpful. If you’re teaching long division, this strategy is a great way for students to learn the skill successfully.

Hi, I’m Jules

Find it fast, browse the blog, visit my teachers pay teachers shop.

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Halloween Color By Number
• Halloween Dot to Dot
• Kindergarten Halloween Sheets
• 1st Grade Halloween Sheets
• Puzzles & Challenges
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• Kindergarten Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Long Division Problems with Answers

(randomly generated).

Welcome to our Long Division Problems with Answers page.

Here you will find our free worksheet generator for generating your own long division sheets and answers.

If you are looking to create your own custom-made long or short division worksheets then look no further!

We also have several worked examples showing long division on this page so you can see how the method works.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Using the random sheet generator will allow you to:

• choose the number range and number of questions you wish the worksheet to have;
• print or save your worksheet and a corresponding answer sheet;
• choose your own title and instructions for completing the sheet - great for homework!

For optimal printing, please set your margins to zero on your print setup options.

To save your worksheets, select Print to PDF in the printing options.

If you have any problems with our Random Generator, please let us know using the Contact Us link at the top of each page.

Mobile View of Worksheets

Please note that our generated worksheets may have problems displaying correctly on some mobile devices.

This should not affect the printing of the sheets which should display correctly.

Long Division Problems with Answers Generator

Here is our random worksheet generator for creating your own long or short division worksheets.

You can generate a range of long division worksheets ranging from 2 digit by 1 digit up to 5 digits by 2 digits.

Using this generator will let you create your own worksheets for:

• Dividing 2, 3, 4 and 5 digit numbers by a range of different numbers up to 99;
• Dividing numbers with or without a remainder;
• Choosing exactly which divisors you want to include;

One of the best features of this generator is that you can choose individual values for the divisors for the worksheets (between 2 and 15).

This means that:

• if you were introducing long division for the first time, you could choose just to divide 2 digit numbers by, say, 2, 3 and 5.
• if you wanted to introduce dividing by two digits but you wanted to divide 3 digit numbers by 11 and 12, you could do that also.
• to access this feature, go to the 'Select divisors from a list' option.

To start creating your sheet, choose an option from the Number values box below.

Parts of a Long Division Equation

The dividend is the number being divided.

The divisor is the number you are dividing by.

The quotient is the number of times the divisor goes into the dividend.

The remainder is what is left over from the dividend when the divisor has been taken away as many times as it can be without leading to a negative answer.

The remainder can be a whole number, but it can also be expressed as a fraction or decimal.

Long Division Problems with Answers Worksheet Generator

4 Steps to Your Worksheets...

• Choose your divisor value - this is the number you are dividing by
• Choose your dividend value - this is the number you are dividing
• Choose if you want to have remainders or not
• Choose the number of questions
• View your sheet
• Print your sheet (if you want to save a hard copy of your sheet, choose 'Save to PDF'.

(Optional) Give your worksheet a title.

(Optional) Write out any instructions to go at the top of the sheet.

Divisor Value:

Remainders:

Dividend value:

Number of Questions:

Your worksheet will appear below.

Examples of Long Division Problems with Answers

Here are some examples showing some long division problems with answers, along with commentary on each step.

Example 1) Work out 84 ÷ 3

So we are working out \[ 3 \enclose {longdiv} {84} \]

FIrst step is to work out 8 ÷ 3, which means we need to find how many groups of 3 make 8.

We can get 2 groups of 3 in 8, and 2 x 3 = 6 so this gives us: \[ \begin {array}{l} \quad 2 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \end{array} \]

Next we subtract 6 from 8 to give us: \[ \begin {array}{l} \quad 2 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 2 \end{array} \]

The next step is to bring down the 4 and put it next to the 2 \[ \begin {array}{l} \quad 2 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 24 \end{array} \]

We now have to work out 24 ÷ 3, or how many groups of 3 make 24.

8 groups of 3 make 24. So this gives us: \[ \begin {array}{l} \quad 28 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 24 \\ \quad \underline{24} \end{array} \]

Finally subtract 24 from 24 to give us an answer of 0. \[ \begin {array}{l} \quad 28 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 24 \\ \quad \underline{24} \\ \quad \; \; 0 \end{array} \]

There are no more digits to bring down and we have no remainders, so we have finished.

Answer: 84 ÷ 3 = 28

Example 2) Work out 347 ÷ 4

So we are working out \[ 4 \enclose {longdiv} {347} \]

FIrst step is to work out 3 ÷ 4, which means we need to find how many groups of 4 make 3.

There are 0 groups of 4 in 3, so we keep the 3 in its place and go on to the next digit which is 4.

This gives us: \[ \begin {array}{l} \quad 0 \\ 4 \enclose {longdiv} {347} \end{array} \]

So the next step is to work out 34 ÷ 4, or find how many groups of 4 make 34.

8 groups of 4 make 32. So this gives us: \[ \begin {array}{l} \quad 08 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \end{array} \]

We subtract 32 from 34 to give us an answer of 2. This gives us: \[ \begin {array}{l} \quad 08 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 2 \end{array} \]

Next we bring the 7 down alongside the 2. \[ \begin {array}{l} \quad 08 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 27 \end{array} \]

So we need to work out 27 ÷ 4, or find how many 4s make 27.

6 groups of 4 make 24. So this gives us: \[ \begin {array}{l} \quad 086 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 27 \\ \quad \; \; \underline {24} \end{array} \]

Finally we need to subtract 24 from 27 to give us 3.

There are no more digits to bring down, so we are left with 3 as a remainder. \[ \begin {array}{l} \quad 086r3 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 27 \\ \quad \; \; \underline {24} \\ \quad \quad 3 \end{array} \]

Answer: 347 ÷ 4 = 86r3

If we wanted the remainder as a fraction, we would have 347 ÷ 4 = 86 ¾

Example 3) Work out 8165 ÷ 12

So we are working out \[ 12 \enclose {longdiv} {8165} \]

FIrst step is to work out 8 ÷ 12, which means we need to find how many groups of 12 make 8.

There are 0 groups of 12 in 8, so we keep the 8 in its place and go on to the next digit which is 1.

This gives us: \[ \begin {array}{l} \quad \; 0 \\ 12 \enclose {longdiv} {8165} \end{array} \]

So the next step is to work out 81 ÷ 12, or find how many groups of 12 make 81.

6 groups of 12 make 72. So this gives us: \[ \begin {array}{l} \quad \; 06 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \end{array} \]

6 groups of 12 make 72. So this gives us: \[ \begin {array}{l} \quad \; 06 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 9 \end{array} \]

Next we bring the 6 down alongside the 9. \[ \begin {array}{l} \quad \; 06 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \end{array} \]

So we need to work out 96 ÷ 12, or find how many 12s make 96.

8 groups of 12 make 96. So this gives us: \[ \begin {array}{l} \quad \; 068 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \end{array} \]

Now we subtract 96 from 96 to give us 0. \[ \begin {array}{l} \quad \; 068 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 0 \end{array} \]

Now we bring down the 5. \[ \begin {array}{l} \quad \; 068 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 05 \end{array} \]

Nexy we need to work out 5 ÷ 12, or how many 12s make 5.

0 groups of 12 make 5, so this gives us: \[ \begin {array}{l} \quad \; 0680 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 05 \\ \qquad \; \: \underline {00} \end{array} \]

Subtracting 0 from 5 gives us 5. There are no more digits to bring down, so 5 is the remainder. \[ \begin {array}{l} \quad \; 0680r5 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 05 \\ \qquad \; \: \underline {00} \\ \qquad \quad 5 \end{array} \]

Answer: 8165 ÷ 12 = 680r5

If we wanted the remainder as a fraction, we would have \[ 8165 \div 12 = 680 {5 \over 12} \]

Other Recommended Worksheets & Resources

Here are some of our other related worksheets you might want to look at.

Long Division Support

We have created a calculator to help you master the long division method.

Just type in the dividend and divisor and let the calculator show you how to work out the long division, step-by-step.

The calculator also gives commentary to show you what is happending at each stage.

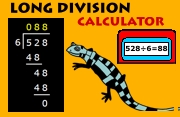
• Step by Step Long Division Calculator

More Randomly Generated Multiplication and Division Worksheets

As well as our long division problems with answers generator on this page, we also have a a generator for making your own division facts and several multiplication worksheet generators.

• Long Division with Money (randomly generated)
• Division Facts Worksheet Generator
• Single Digit Multiplication Worksheets Generator
• Multi Digit Multiplication Generator
• Money Multiplication Worksheets Generator

Graded (non-generated) Division Sheets

As well as our randomly generated long division worksheets, we also have a selection of carefully graded division worksheets for each grade.

These sheets are especially useful for introducing the concept and keeping the numbers to divide manageable and simple.

The sheets in the links below are not randomly generated, but have been carefully selected to progress your child through their division learning.

Learning long division starts at a 3rd grade level with learning to divide by a single digit. It then gradually gets more complex for higher grades.

Long Division Worksheets (graded)

• Long Division Worksheets 3rd Grade
• 4th Grade Long Division Worksheets
• Long Division Worksheets 5th Grade
• Long Division of Decimal Numbers

Mental Division Worksheets

As well as long division worksheets, you also need to know your division facts.

Knowing your division facts will help improve the speed and accuracy of your long division.

We have a wide variety of division fact worksheets for you to choose from.

Division Facts Worksheets

Division facts starts off with understanding the link between multiplication and division.

Once you understand this, you can start learning the division facts related to the multiplication table.

After this, at a 4th and 5th grade level, you can start learning related division facts.

This means that if you know that 12 ÷ 4 = 3 then you can work out 120 ÷ 4 = 30 or that 120 ÷ 40 = 3, etc

• Understanding Division Sheets (2nd grade)
• Division Facts to 10x10 Worksheets (3rd grade)
• Divding by Multiples of 10 and 100 Worksheets (4th grade)
• Decimal Division Facts (5th grade)

Multiply and Divide by 10 and 100

Knowing how to multiply and divide numbers by 10 and 100 is a very useful skill.

It is especially useful when converting between metric units or when using percentages.

• Multiply and Divide by 10 and 100 (decimals)

Division Math Games

Here you will find a range of Free Division Games.

The following games develop the Math skill of dividing and learning your division facts in a fun and motivating way.

Using these sheets will help your child to:

• learn their division facts;
• develop their strategic thinking skills.
• Math Division Games

Return to Division Worksheets

Return to Math Worksheets Generator

Return from Long Division Problems with Answers to Math Salamanders Home Page

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

We're sorry, but we don't support Internet Explorer anymore. Please use a different browser .

Long Division

Online practice for grades 4-6.

Practice long division problems step-by-step interactively and online!

Each long division problem is presented in a grid, and you can write numbers and calculate the remainders just like if you were using paper and pencil.

You can choose the number of digits for the dividend and for the divisor (actually, a range for the number of digits), to make the problems easier or more challenging.

- For fourth grade: choose single-digit divisors and 2-4 digit dividends

- For fifth grade: choose single and two-digit divisors, and 3-6 digit dividends

At any point of your practice problem, you can push the "Check" button to check your work thus far. Any wrong digits are marked red, and correct ones are marked green.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Understanding multiplication

Understanding division

Long division

Here you will learn about long division, including how to divide using long division and solving for quotients with and without remainders.

Students will first learn about long division as part of the number system in grade 6 and will continue to use the skill throughout middle school and high school.

What is long division?

Long division , also known as the standard algorithm, is a standardized process used to divide multi-digit numbers, by breaking the multiplication into a sequence of steps.

Before performing long division, you must first understand the different parts of a division equation:

• The dividend is the number that is being divided equally.
• The divisor is the number that divides the dividend. It is also thought of as the number of items in each group, or the number of groups.
• The quotient is the answer of the division process. In some cases, there may be a remainder included with the quotient.

For example, if we were to divide 120 \div 6,

How to divide using long division

In order to divide using long division, first identify the dividend and divisor. You will write the dividend under a division bracket, with the divisor to the left.

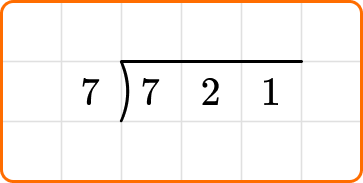
You will then start a sequence of steps that include dividing, multiplying and subtraction. These steps can be done once, or many times, depending on the size of the divisor and dividend.

Divide : First, calculate how many times the divisor 7 can divide into the first digit of the dividend, 7.

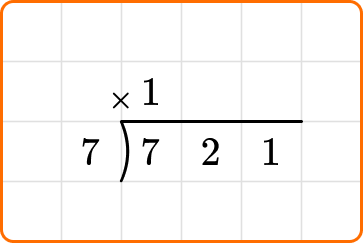
Multiply : The 1 will be placed above the top line of the division bracket, and multiplied by the divisor, 7.

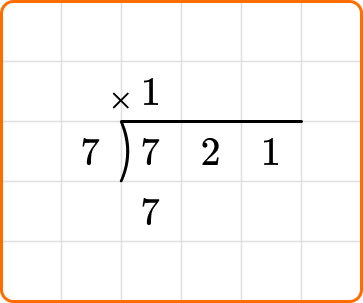
Subtract : Place this number under the first number in the hundreds place, 7 and subtract.

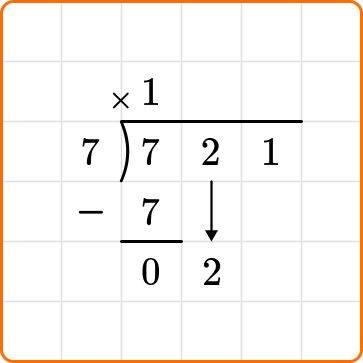
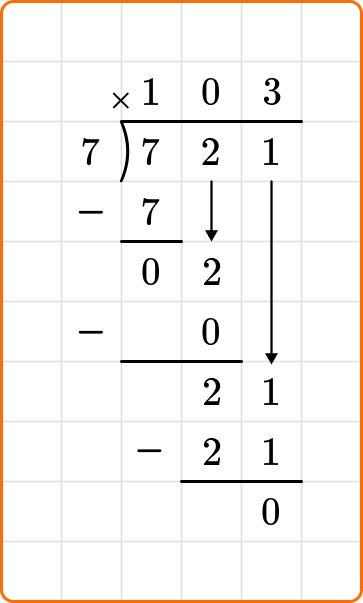
Bring down the next number from the dividend, and continue dividing until all numbers in the dividend have been brought down.

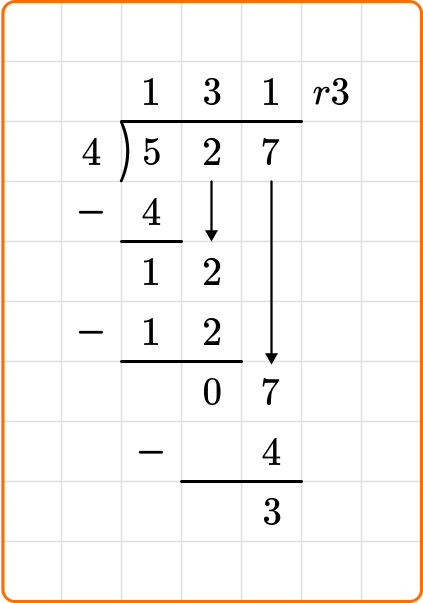
Quotients with remainders

Sometimes the dividend cannot be equally divided into by the divisor. When this happens, you would be left with a remainder. You may see a remainder in different formats:

• As a whole number
• As a decimal
• As a fraction

Students in upper grade levels are often taught to leave the reminders as either whole numbers or fractions. As students move into long division in middle school, students will be expected to express their remainders as fractions.

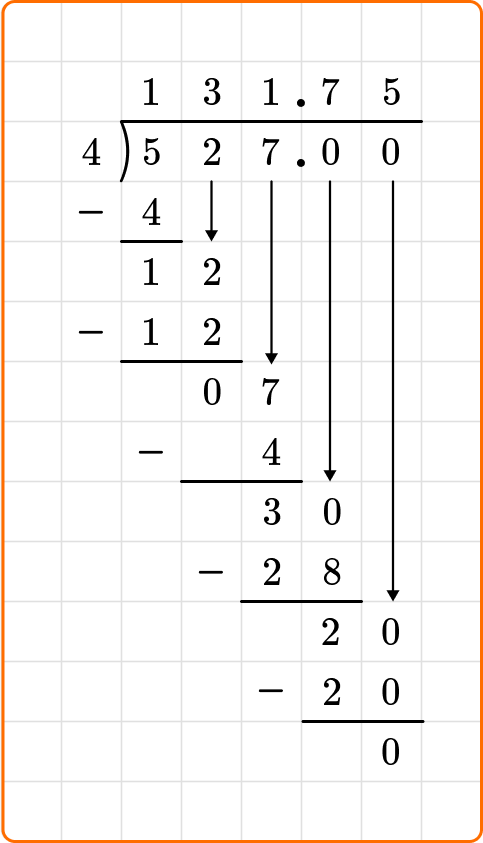
If you divide 527 \div 4, you will end up with a remainder of 3. Let’s look at how you can show the remainder of 3 in all three ways:

Remainders as a whole number

When you leave the remainder as a whole number, you will write a lowercase r to the right of the quotient, and place the remainder after.

For example,

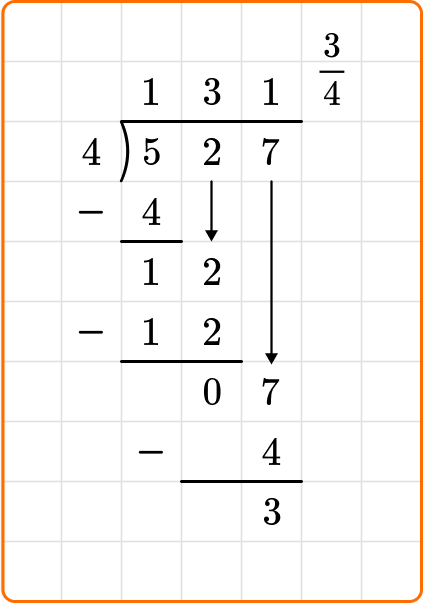
Remainders as a fraction

When you leave your remainder as a fraction, you will write the remainder as the numerator, and the divisor as the denominator.

Remainder as a decimal

When asked to leave your remainder as a decimal, you will continue dividing. First, you will place a decimal to the left of the ones place of the dividend, as well as in the quotient. After the decimal place next to the dividend, place a zero.

You will then bring that zero down, as you had all the digits from the dividend, and continue dividing until you get a remainder of zero.

Common Core State Standards

How does this relate to 6 th and 7 th grade math?

• Grade 6 – The Number System (6.NS.B.2) Fluently divide multi-digit numbers using the standard algorithm.
• Grade 7 – The Number System (7.NS.A.2d) Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.

[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)

Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4th, 5th and 7th grade multiplication and division topics to identify areas of strength and support!

In order to divide using long division, you need to:

Set up the division equation using a division bracket.

Divide, multiply and subtract.

Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor.

State your answer.

Long division examples

Example 1: long division without remainders.

Solve 672 \div 6.

Write the dividend, 672, inside the division bracket, and the divisor, 6, out to the left of the division bracket.

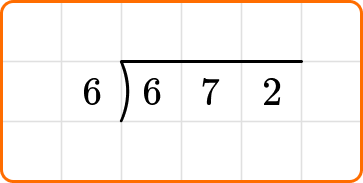
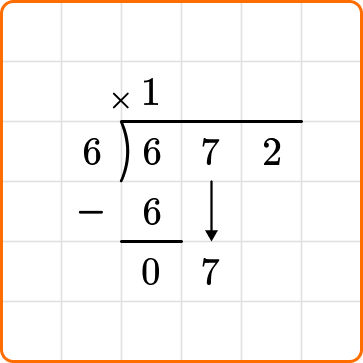
2 Divide, multiply and subtract.

Ask yourself: How many times does 6 go into the first digit of the dividend 6?

Divide: 6 \div 6=1

Write the number 1 above the long division symbol.

Multiply: 6 \times 1=6

Write the result beneath the dividend.

Subtract: 6-6=0

Bring down the next digit of the dividend, the 7.

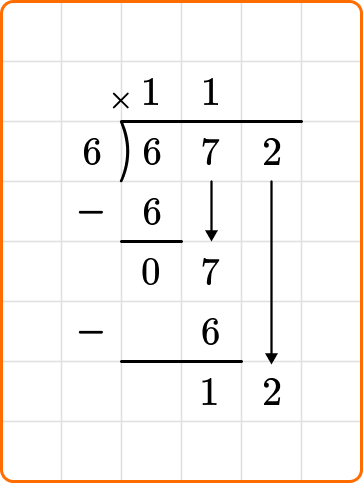
3 Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor.

Ask yourself: How many times does 6 go into 7?

Divide: 7 \div 6=1

Subtract: 7-6=1

Bring down the next digit of the dividend, 2, beside the 1.

12 is larger than the divisor 6, so continue dividing.

Ask yourself: How many times does 6 go into 12?

Divide: 12 \div 6=2

Write the number 2 above the long division symbol.

Multiply: 6 \times 2=12

Subtract: 12-12=0

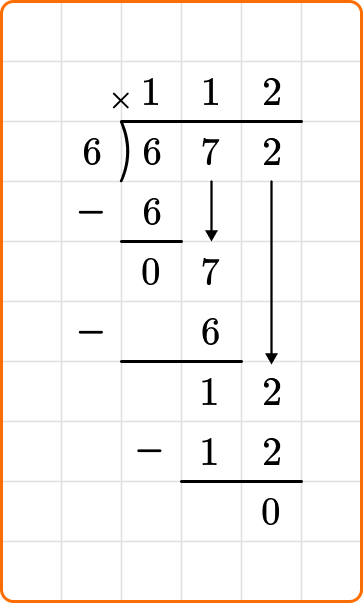
There is no remaining value to divide, so you are done dividing. The quotient is the number on the top of the division bracket.

4 State your answer.

Example 2: long division without remainders

Solve 9,240 \div 30.

Write the dividend, 9,240, inside the division bracket, and the divisor, 30, out to the left of the division bracket.

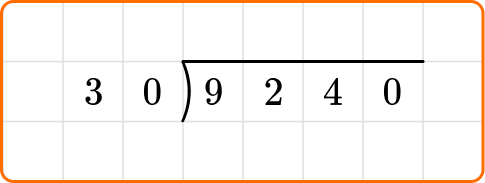
Ask yourself: How many times can 30 go into 92?

Divide: 92 \div 30=3

Write the number 3 above the long division symbol.

Multiply: 30 \times 3=90

Subtract: 92-90=2

Bring down the next digit of the dividend, 4, beside the 2.

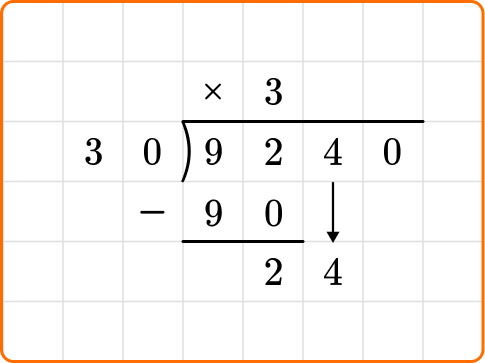
Ask yourself: How many times does 30 go into 24?

Divide: 24 \div 30=0

Write the number 0 above the long division symbol.

Multiply: 30 \times 0=0

Subtract: 24-0=24

Bring down the remaining dividend, 0, and you are left with 240.

240 is larger than the divisor 30, so continue dividing.

Ask yourself: How many times 30 goes into 240?

Divide: 240 \div 30=8

Write the number 8 above the long division symbol.

Multiply: 30 \times 8=240

Subtract: 240-240=0

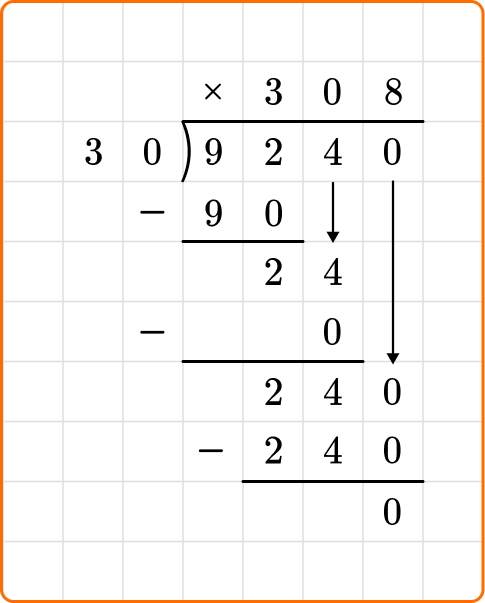
Example 3: long division with whole number remainders

Solve 763 \div 28. Write the remainder as a whole number.

Write the dividend, 763, inside the division bracket, and the divisor, 28, out to the left of the division bracket.

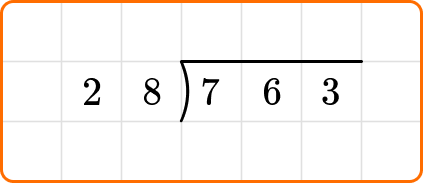
Ask yourself: How many times does 28 go into the first two digits of the dividend, 76?

Divide: 76 \div 28=2

Multiply: 28 \times 2=56

Subtract: 76-56=20

Bring down the next digit of the dividend, the 3.

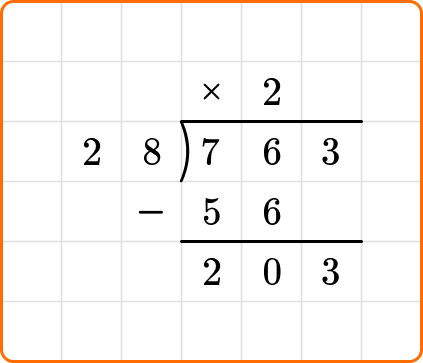
Ask yourself: How many times does 28 go into 203?

Divide: 203 \div 28=7

Write the number 7 above the long division symbol.

Multiply: 28 \times 7=196

Subtract: 203-196=7

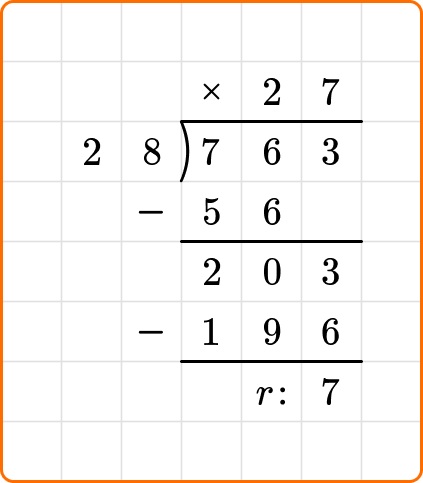
7 is less than the divisor 28, so you are finished dividing.

The question states to write your remainder as a whole number.

763 \div 28=27 \; r7

Example 4: long division with remainders as fractions

Solve 167 \div 8. Write your remainder as a fraction.

Write the dividend, 167, inside the division bracket, and the divisor, 8, out to the left of the division bracket.

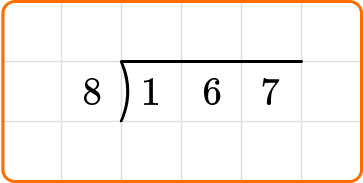
Ask yourself: How many times does 8 go into the first two digits of the dividend, 16?

Divide: 16 \div 8=2

Multiply: 8 \times 2=16

Subtract: 16-16=0

Bring down the next digit of the dividend, 7, beside the 0.

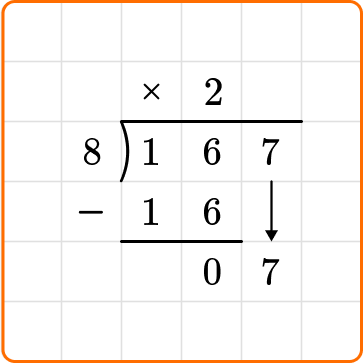
Ask yourself: How many times does 8 go into 7?

Divide: 7 \div 8=0

Multiply: 0 \times 8=0

Subtract: 7-0=7

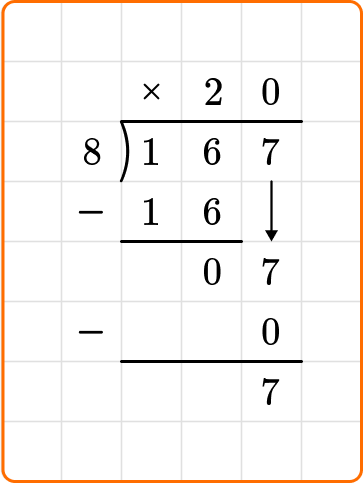
7 is less than 8, so you are done dividing.

To write your remainder as a fraction, the remainder is the numerator and the divisor becomes your denominator.

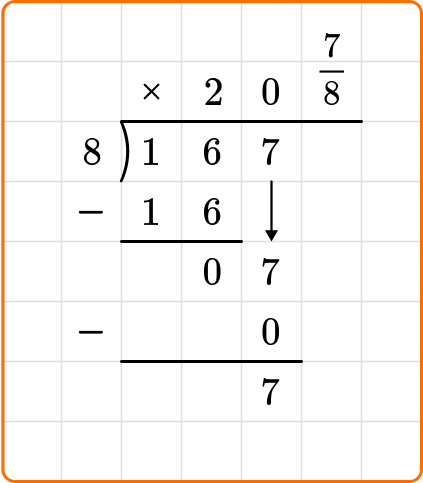
The question states to write your remainder as a fraction.

167 \div 8=20 \cfrac{7}{8}

Example 5: long division with a decimal remainder

Solve 53 \div 4. Write your remainder as a decimal.

Write the dividend, 53, inside the division bracket, and the divisor, 4, out to the left of the division bracket.

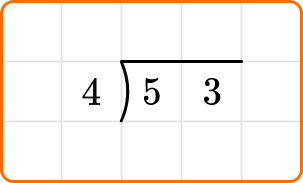
Ask yourself: How many times does 4 go into the first digit of the dividend, 5?

Divide: 5 \div 4=1

Multiply: 4 \times 1=4

Subtract: 5-4=1

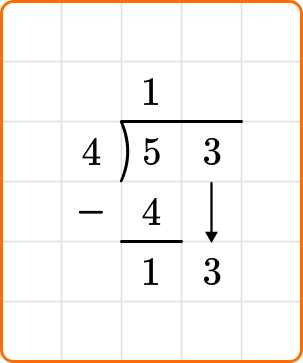
Ask yourself: How many times does 4 go into 13?

Divide: 13 \div 4=3

Multiply: 4 \times 3=12

Subtract: 13-12=1

Because the problem states to write the remainder as a decimal, you will keep dividing, even though the remainder is less than the divisor.

You will add a decimal point after the 3 in 53, followed by a 0. Make sure to write the decimal point above the division bracket too. Bring the zero down next to the 1 and continue dividing.

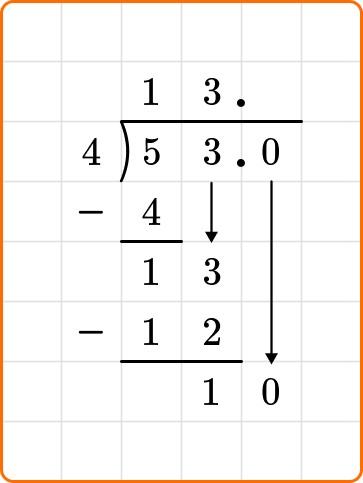
Ask yourself: How many times does 4 go into 10?

Divide: 10 \div 4=2

Write the number 2 above the division symbol, to the right of the decimal point.

Multiply: 4 \times 2=8

Subtract: 10-8=2

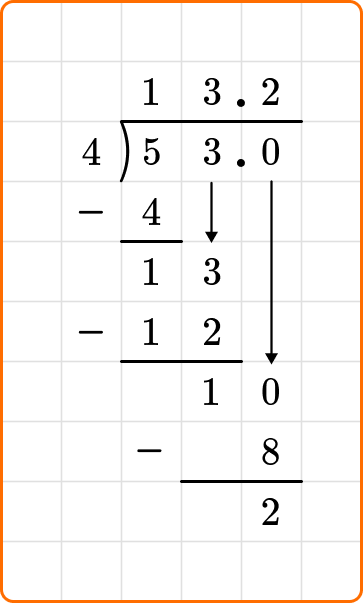
You will repeat the process of adding another zero to the dividend and bring it down until you have a zero after subtracting.

Ask yourself: How many times does 4 go into 20?

Divide: 20 \div 4=5

Write the number 5 above the long division symbol.

Multiply: 4 \times 5=20

Subtract: 20-20=0

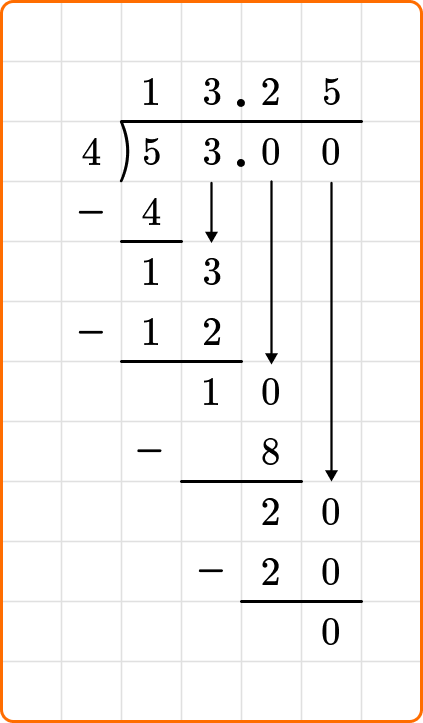
The problem states to write your remainder as a decimal.

53 \div 4=13.25

Example 6: long division word problem

Cassie received \$1,260 for her graduation. She wants to spend the money equally over the next 6 months. How much money can Cassie spend each month?

Write the dividend, 1,260, inside the division bracket, and the divisor, 6, out to the left of the division bracket.

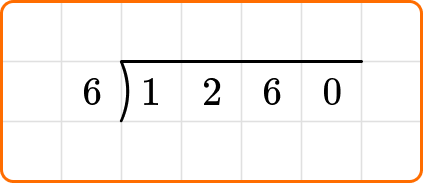
Bring down the next digit of the dividend, the 6.

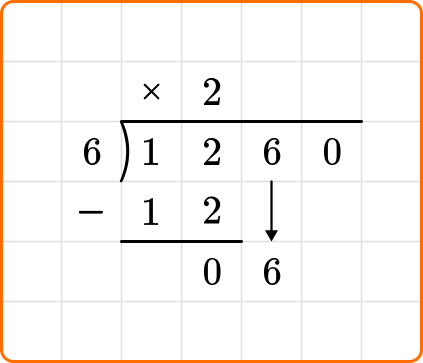
Ask yourself: How many times does 6 go into 6?

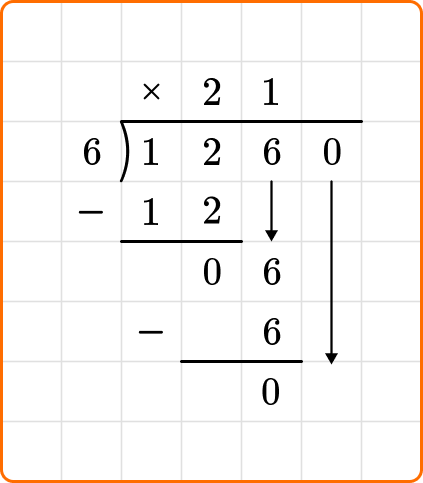
Ask yourself: How many times does 6 go into 0?

Divide: 6 \div 0=0

Multiply: 6 \times 0=0

Subtract: 0-0=0

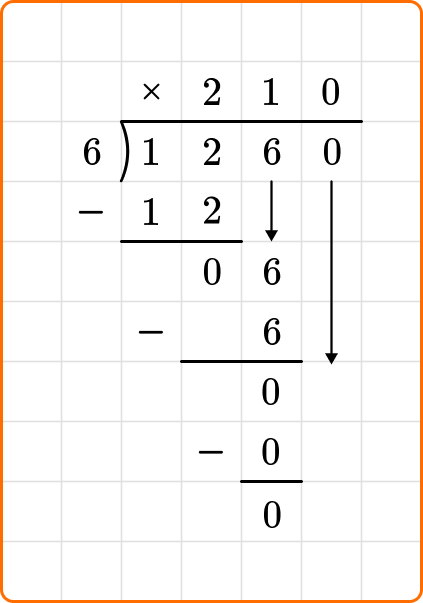
Cassie can spend \$210 each month.

1260 \div 6=210

Teaching tips for long division

• Make sure students have a firm grasp on how to divide using partial quotients, as it helps students visualize why the long division method works.
• If using long division worksheets, start with simple long division problems, such as dividing by one digit divisors with no remainders. Once students begin grasping the concept of long division, increase the challenge of the problems, including large numbers.
• Emphasize paying attention to the place value of each digit as they set up and solve the problem. Allowing students to use graph paper when first beginning long division will allow them to easily organize their math, especially when working with larger numbers.
• Providing the students with step-by-step division steps allows them to refer back to them as needed. These can be displayed within the classroom on an anchor chart or in their math journals.
• Allow students to check their answers using a long division calculator. This allows real time feedback for students so they do not continue to practice the long division algorithm incorrectly.

Easy mistakes to make

• Forgetting to bring down the next number Students will divide the first set of numbers correctly but may forget they need to bring down the next digit from the dividend to continue dividing. Having an example of a complete long division problem will give students something to refer back to.
• Alignment issues Proper placement of numbers is important and can lead to calculation errors if the work is not organized. Allowing students to use graph paper is one way to assist with this.

Related multiplication and division lessons

• Negative numbers
• Negative times negative
• Multiplying and dividing integers
• Multiplying and dividing rational numbers
• Multiplying multi digit numbers
• Multiplicative comparison
• Dividing multi digit numbers
• Multiplication

Practice long division questions

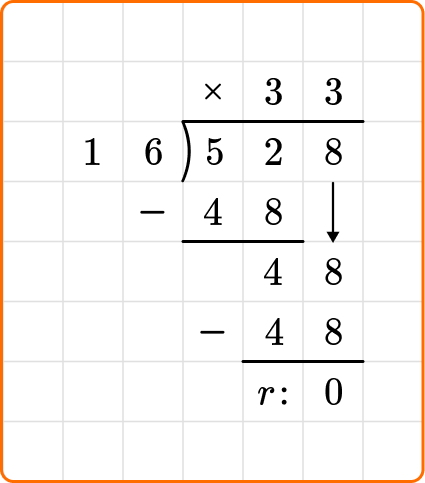
1. Solve 528 \div 16.

Set up your division equation with the dividend, 528, inside the division bracket and the divisor, 16, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 16.

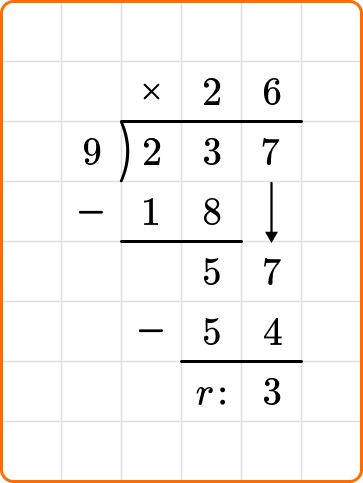
2. Divide 237 \div 9.

Set up your division equation with the dividend, 237, inside the division bracket and the divisor, 9, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 9.

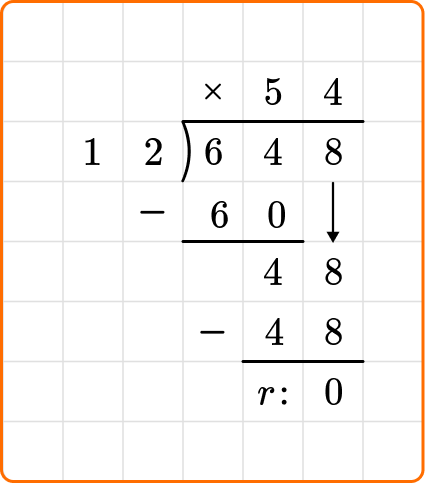
3. Solve 648 \div 12.

Set up your division equation with the dividend, 648, inside the division bracket and the divisor, 12, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 12.

4. Solve 489 \div 15. Write the quotient as a decimal.

Set up your division equation with the dividend, 489, inside the division bracket and the divisor, 15, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0, leaving your remainder as a decimal.

5. Solve 357 \div 8. Write the quotient as a fraction.

Set up your division equation with the dividend, 357, inside the division bracket and the divisor, 8, to the left.

Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0, leaving your remainder as a fraction.

6. Mrs. Davis had 112 pencils to divide into 9 pencil boxes. How many pencils did Mrs. Davis put in each pencil box?

Set up your division equation with the dividend, 112, inside the division bracket and the divisor, 9, to the left.

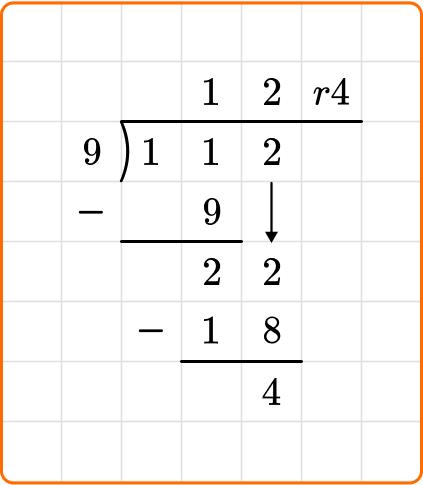
Mrs. Davis can equally place 12 pencils in each pencil box and will have 4 pencils left over.

Long division FAQs

The number of decimal places will vary by division problem. Some division problems will only have one decimal place, while others will have many.

The long division symbol is sometimes called a division bracket, but does not have an established name.

The next lessons are

• Types of numbers
• Rounding numbers
• Factors and multiples

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview