area problem solving questions

• Maths Questions

Area Questions

Students can easily access a variety of area questions with complete explanations, which are provided below. One of the most fundamental concepts taught in elementary and secondary schools is the concept of areas of different shapes. NCERT curriculum is used to frame the questions. Students can use these questions to get a fast overview of the topics and practise them so that they will become more knowledgeable about the concept. To cross-verify your answers, look over the complete explanations for each question. To learn more about areas of different shapes, click here .

Go through the different types of area questions and practise them to learn the concept well.

Area Questions with Solutions

1. Find the area of a circle if its diameter is 42 cm. (Use π = 22/7 )

Given: Diameter, d = 42 cm.

Hence, Radius, r = d/2 = 42/2 = 21 cm

We know that the area of a circle = πr 2 square units.

A = (22/7) × 21 × 21

A = 22 × 3 × 21

A = 1386 cm 2 .

Therefore, the area of the circle = 1386 cm 2 .

2. Calculate the radius of a circle if its area is 25π m 2 .

Given: Area = 25π m 2

We know that area of a circle = πr 2

Hence, we can write,

Hence, r = 5 m

Therefore, the radius of the circle is 5 m.

3. Find the area of a square whose side length is 7 cm.

Given, Side, a = 7 cm.

As we know, the area of square = a 2 square units

A = 7 2 cm 2

A = 49 cm 2

Hence, the area of the square is 49 cm 2 .

4. Compute the side length of a square, if its area is 121 cm 2 .

Given: Area of a square = 121 cm 2 .

We know that, A = side 2 square units

121 = side 2

Side = 11 cm

Therefore, the side length of the square is 11 cm, if its area is 121 cm 2 .

5. Determine the area of a rectangle, if its length is 11 cm and breadth is 9 cm.

Given: Length = 11 cm

Breadth = 9 cm.

We know that the formula to find the area of a rectangle is:

Area = Length × Breadth square units

Area = 11 × 9 cm 2

Area = 99 cm 2

Therefore, the area of the rectangle is 99 cm 2 .

6. Compute the breadth of a rectangle if its area is 84m 2 and length is 12 m.

Area of a rectangle = 84 m 2

Length = 12 m

As we know,

Rectangle’s area = Length × Breadth

84 = 12 × Breadth

Therefore, Breadth = 84/12

Breadth = 7 m.

Hence, the breadth of the rectangle is 7 m if its area is 84 m 2 and length is 12 m.

7. Find the area of a parallelogram, if its base length is 9 cm and height is 5 cm.

Given: Base length = 9 cm

Height = 5 cm.

The formula to calculate the area of a parallelogram is:

Area = Base × Height square units.

On substituting the given values, we get

Area = 9 × 5 cm 2

Area = 45 cm 2

Therefore, the area of the parallelogram is 45 cm 2 .

8. Compute the area of a triangle, if its base measurement is 6 cm and height is 10 cm.

Given: Base, b = 6 cm

Height, h = 10 cm.

We know that the area of a triangle = (½) × b × h square units.

Now, substitute the given values, we get

A = ½ × 6 × 10 cm 2

A = 3 × 10 cm 2

A = 30 cm 2

Therefore, the area of the triangle is 30 cm 2 .

9. Determine the height of a triangle, if its base length is 8 cm and its area is 52 cm 2 .

Given: Base length, b = 8 cm

Area = 52 cm 2

As we know, the area of a triangle is ½ bh square units

52 = (½) × 8 × h

52 × 2 = 8 × h

104 = 8 × h

Hence, the height of the triangle is 13 cm if its base is 8 cm and its area is 52 cm 2 .

10. Determine the area of a rhombus if its diagonals are 7 cm and 10 cm.

Diagonal 1 = 7 cm

Diagonal 2 = 10 cm

The area of a rhombus = ½ × diagonal 1 × diagonal 2

Now, substitute the values, we get;

Area = ½ × 7 × 10 cm 2

Area = 7 × 5 cm 2

Area = 35 cm 2

Therefore, the area of the rhombus is 35 cm 2 , if its diagonals are 7 cm and 10 cm.

Explore More Articles:

• Area of Triangle
• Area of Circle
• Area of Rhombus
• Rectangle Questions
• Area of Parallelogram Questions
• Quadrilaterals Questions
• Geometry Questions

Practice Questions

• Compute the area of a triangle, if its base is 14 cm and height is 10 cm.
• Determine the area of a rectangle if its length is 17 cm and breadth is 15 cm.
• Find the area of a square whose side measures 19 cm.

To learn all Maths-related concepts, download BYJU’S – The Learning APP today and explore more interesting videos.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

REAL WORLD PROBLEMS INVOLVING AREA AND PERIMETER

Problem 1 :

The diagram shows the shape and  dimensions of Teresa’s rose garden.

(a) Find the area of the garden.

(b) Teresa wants to buy mulch for her garden. One bag of mulch covers  12 square feet. How many bags will she need?

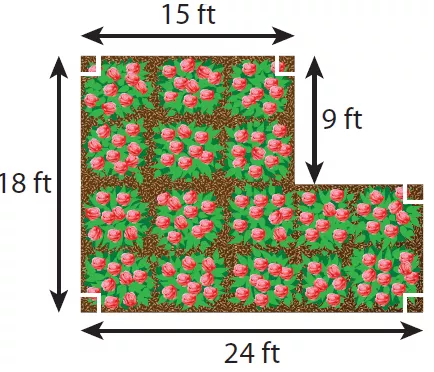
By drawing a horizontal line, we can divide the given shape into two parts as shown below.

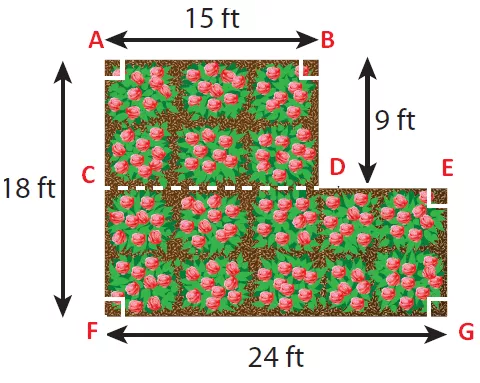
(1) ABCD is a rectangle

(2) CEFG is also a rectangle

Area of the garden

= Area of rectangle ABCD + Area of the rectangle CEFG

Area of rectangle ABCD :

length AB = 15 ft and width BD = 9 ft

= length x width 

 =  15 x 9

=  135 ft ²  ----(1)

Area of rectangle CEFG :

length CE = 24 ft and width CF = AF - AC ==> 18 - 9 = 9 ft

 =  24 x 9

=  216 ft ²  ----(1)

(1) + (2) 

Area of the rose garden = 135 + 216 ==> 351 ft ²

Number of bags that she needed = 351/12 ==> 29.25

So, she will need 30 bags of mulch

Problem 2 :

The length of a rectangle is 4 less than 3 times its width. If its length is 11 cm, then find the perimeter. 

Let w be the width of the rectangle.

Then, its length is (3w - 4).

Given : Length is 11 cm. 

Then, 

Length (l)  =  11

3w - 4  =  11

3w  =  15

w  =  5

So, the perimeter of the rectangle is 

=  2(l + w)

=  2(11 + 5)

=  2(16)

=  32 cm

Problem 3 :

The diagram shows the floor plan of a hotel  lobby. Carpet costs $3 per square foot. How  much will it cost to carpet the lobby?

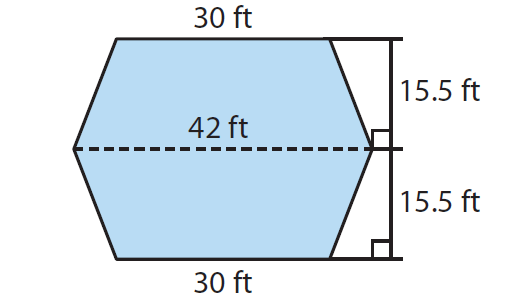
By observing the above picture, we can find two trapeziums of same size. Since both are having same size. We can find area of one trapezium and multiply the area by 2.

Area of trapezium = (1/2) h (a +  b)

h = 15.5 ft  a = 30 ft  and b = 42 ft

  =  (1/2) x 15.5 x (30 + 42)

  =  (1/2) x 15.5 x 72 ==> 15.5 x 36==> 558 square feet

Area of floor of a hotel  lobby = 2 x 558

 =  1116 square feet

Cost of carper per square feet = $3

=  3 x 1116 ==> $ 3348

Amount spent for carpet =    $ 3348.

Problem 4 :

The cost of fencing a circle shaped garden is $20 per foot. If the radius of the garden is 14 feet, find the total cost of fencing the garden. ( π  =  22/7).  

To know the length of fencing required, find the circumference of the circle shaped garden.

Circumference of the circle shaped garden is 

=  2πr

Substitute 22/7 for π and 14 for r. 

=  2(22/7)(14)

=  88 feet

Total cost of fencing is 

=  88(20)

=  $1760

Problem 5 :

Jess is painting a giant arrow on a playground. Find the area of  the giant arrow. If one can of paint covers 100 square feet,  how many cans should Jess buy?

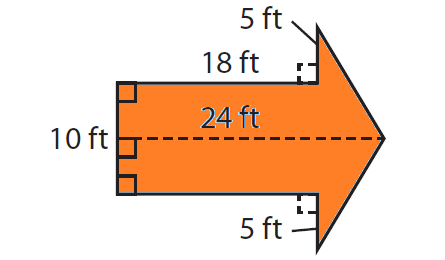
Now we are going to divide this into three shapes. Two triangles and one rectangle.

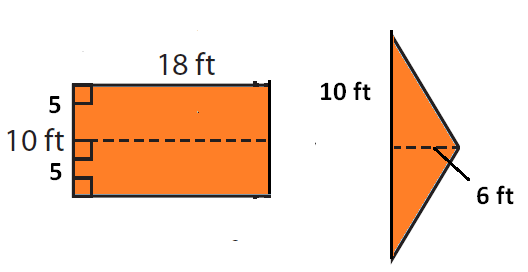
Area of rectangle = length x width

   =  18 x 10 ==> 180 square feet

Area of one triangle = (1/2) x b x h

   =  (1/2) x 6 x 10 ==> 30 square feet

Area of two triangles = 2 x 30 = 60 square feet

Total area of the given shape = 180 + 60

=   240 square feet

one can of paint covers 100 square feet

Number of cans needed = 240/100 = 2.4 approximately 3.

So, Jessy has to 3 cans of paint.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

AP Precalculus Problems and Solutions (Part - 1)

Oct 30, 24 10:07 AM

SAT Math Resources (Videos, Concepts, Worksheets and More)

Oct 29, 24 06:24 AM

Digital SAT Math Problems and Solutions (Part - 61)

Oct 29, 24 06:23 AM

Reset password New user? Sign up

Existing user? Log in

Length and Area Problem Solving

Already have an account? Log in here.

• A Former Brilliant Member

To solve problems on this page, you should be familiar with the following: Perimeter Area of Triangle Area of Rectangles Area of Circles

You should also know the following formulas:

• Square with side length \(L\): Area is \(L^2\), and perimeter is \(4L \).
• Rectangle with side length \(L\) and breadth \(B\): Area is \(L\times B\), and perimeter is \(2(L+B) \).
• Equilateral triangle with side length \(s\): Area is \( \frac {\sqrt3}4 s^2 \), and perimeter is \(3s\).

If the area of a square is 144, what is the perimeter of the square? ANSWER Let \(L\) denote the area of the square, then \(L^2 = 144 = 12^2 \) or \(L =12\). Note that we are only taking the positive root because \(L\) represents a physical dimension. Thus the perimeter of the square is \(4L = 4\times 12= 48. \ _\square\)

The ancients talked about "squaring the circle," by creating a square and a circle which have the same area. If the radius of the circle is 1, what would be the side length of the square? ANSWER Let the side length of the square be \( S \). Then, we are given that \( S^2 = \pi \times 1 ^2 = \pi \). Taking square roots, we obtain \( S = \sqrt{\pi } \). \(_\square\)

If the ratio of the area of a square to the area of an equilateral triangle is \( 4 : 3 \), what is the ratio of the side length of the square to the side length of the equilateral triangle? Let the side length of the square be \(S\). Then the area of the square is \(S^2 \). Let the side length of the equilateral triangle be \(T \). Then the area of the equilaterial triangle is \( \frac{ \sqrt{3}} {4} T^2 \). We are given that \( \frac{ S^2 } { \frac{ \sqrt{3}} {4} T^2 } = \frac{4}{3} \), or that \( \frac{ S^2 }{ T^2 } = \frac{ \sqrt3 } { 3 } \). Taking square roots on both sides, \( \frac{ S } { T} = \frac1{3^{1/4}} \). \(_\square\)

If a square and a circle have the same perimeter, which of them will have a greater area? ANSWER Let the radius of the circle be \(r\) and the side length of the square be \(s\). Then \[2\pi r=4s \Rightarrow r=\dfrac{2s}{\pi}.\] Now the area of the square is \(s^2,\) and the area of the circle is \(\pi r^2 = \pi \times \left(\dfrac{2s}{\pi}\right)^2=\dfrac{4s^2}{\pi}.\) Then the ratio of the area of the square to the area of the circle is \(\dfrac{s^2}{\hspace{2mm} \frac{4s^2}{\pi}\hspace{2mm} } = \dfrac{\pi}{4} <1.\) Hence, the circle has a larger area. \(_\square\)

Line segments are drawn from the vertices of the large square to the midpoints of the opposite sides to form a smaller, white square.

If each red or blue line-segment measures \(10\) m long, what is the area of the smaller, white square in m\(^{2}?\)

A triangle, a square, a pentagon, a hexagon, an octagon, and a circle all have the same perimeter.

Which one has the smallest area?

Note: All of the polygons are regular.

Four squares of respective side lengths 4, 9,15, and 21 are arranged as shown. Find the length of the yellow line. If your answer can be expressed as \(\frac{a}{7}+\frac{b}{7}\sqrt{c}\), where \(c\) is square free, give \(a+b+c.\)

Note: Neglect the thickness of the lines.

Problem Loading...

Note Loading...

Set Loading...

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Geometry >
• Rectangles >

Word Problems Worksheets | Area of Rectangles

Promote mathematical interest in children of grade 3 through grade 6 by relating the concept to the real-life situation with this batch of printable word problems worksheets on area of rectangles. The word problems offer two levels of difficulty; level 1 comprises word problems to find the area of rectangles and the missing parameters, while level 2 has scenarios to find the area involving unit conversions or finding the cost. Also, included here are word problems to find the area of rectangular shapes. Delve into practice with the free worksheets here!

Area Word Problems | Level 1

Equip children to bring together reality and math with these pdf word problems on area of rectangles. Instruct 3rd grade and 4th grade kids to plug in the dimensions in the formula A = length * width to compute the area.

• Download the set

Area Word Problems | Level 2

Visualize the scenario and highlight the length and width. Children are expected to convert to the specified units and then solve for the area of rectangles. Some word problems require calculating the cost.

Find the Missing Length or Width | Level 1

Direct children of grade 4 and grade 5 to figure out the area and the length or width in each word problem. Rearrange the rectangle formula, making the missing dimension the subject, substitute and solve for length or width.

Find the Missing Length or Width | Level 2

Level up with this set of printable worksheets featuring word problems to solve for the unknown dimension using the area and the dimension given. The word problems involve either unit conversion or determining the cost to provide ample practice for 5th grade and 6th grade children.

Area of Rectangular Paths | Word Problems

Read the scenario and draw the rectangular path, decompose the path into non-overlapping rectangles and find the area of each individual rectangle, add the areas to determine the area of the rectangular paths in this set of pdf worksheets.

Related Worksheets

» Area of Squares

» Area of Parallelograms

» Area of Quadrilaterals

» Area of Polygons

» Rectangles

Become a Member

Membership Information

Printing Help

How to Use Online Worksheets

How to Use Printable Worksheets

Privacy Policy

Terms of Use

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!