solving assignment problem

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

Problem Formulation

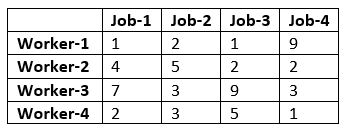
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.  

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Blending Problem in Python using Gurobi
• Transshipment Problem in Python Using PuLP

You May Also Like

Solving Linear Programming using Python PuLP

Dimensionality Reduction using tSNE

Agglomerative Clustering

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

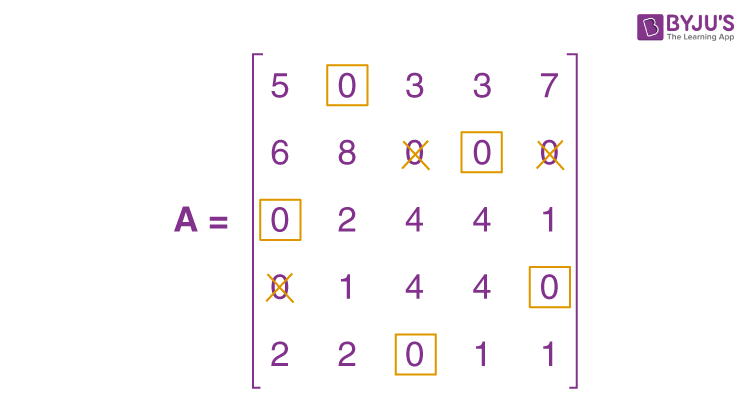
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

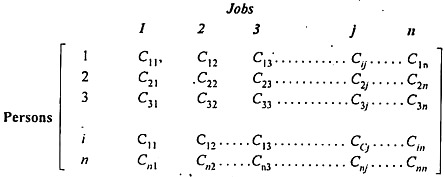
• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Similar Reads

• Mathematical

Please Login to comment...

Improve your coding skills with practice.

What kind of Experience do you want to share?

Assignment Problem: Maximization

There are problems where certain facilities have to be assigned to a number of jobs, so as to maximize the overall performance of the assignment.

The Hungarian Method can also solve such assignment problems , as it is easy to obtain an equivalent minimization problem by converting every number in the matrix to an opportunity loss.

The conversion is accomplished by subtracting all the elements of the given matrix from the highest element. It turns out that minimizing opportunity loss produces the same assignment solution as the original maximization problem.

• Unbalanced Assignment Problem
• Multiple Optimal Solutions

Example: Maximization In An Assignment Problem

At the head office of www.universalteacherpublications.com there are five registration counters. Five persons are available for service.

How should the counters be assigned to persons so as to maximize the profit ?

Here, the highest value is 62. So we subtract each value from 62. The conversion is shown in the following table.

On small screens, scroll horizontally to view full calculation

Now the above problem can be easily solved by Hungarian method . After applying steps 1 to 3 of the Hungarian method, we get the following matrix.

Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix.

Select the smallest element from all the uncovered elements, i.e., 4. Subtract this element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment. Repeating step 3, we obtain a solution which is shown in the following table.

Final Table: Maximization Problem

Use Horizontal Scrollbar to View Full Table Calculation

The total cost of assignment = 1C + 2E + 3A + 4D + 5B

Substituting values from original table: 40 + 36 + 40 + 36 + 62 = 214.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem