null hypothesis statistical testing example

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

Knowledge Base
Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

Null hypothesis (H 0 ): There’s no effect in the population .
Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

	( )

Does tooth flossing affect the number of cavities?	Tooth flossing has on the number of cavities.	test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ .
Does the amount of text highlighted in the textbook affect exam scores?	The amount of text highlighted in the textbook has on exam scores.	: There is no relationship between the amount of text highlighted and exam scores in the population; β = 0.
Does daily meditation decrease the incidence of depression?	Daily meditation the incidence of depression.*	test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ .

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.



Does tooth flossing affect the number of cavities?	Tooth flossing has an on the number of cavities.	test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ .
Does the amount of text highlighted in a textbook affect exam scores?	The amount of text highlighted in the textbook has an on exam scores.	: There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0.
Does daily meditation decrease the incidence of depression?	Daily meditation the incidence of depression.	test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < .

Null and alternative hypotheses are similar in some ways:

They’re both answers to the research question
They both make claims about the population
They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.


	A claim that there is in the population.	A claim that there is in the population.


	Equality symbol (=, ≥, or ≤)	Inequality symbol (≠, <, or >)
	Rejected	Supported
	Failed to reject	Not supported

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

	( )
test with two groups	The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ .	The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ .
with three groups	The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ .	The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population.
	There is no correlation between independent variable and dependent variable in the population; ρ = 0.	There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0.
	There is no relationship between independent variable and dependent variable in the population; β = 0.	There is a relationship between independent variable and dependent variable in the population; β ≠ 0.
Two-proportions test	The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = .	The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ .

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 27 September 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :


equal (=)	not equal (≠) greater than (>) less than (<)
greater than or equal to (≥)	less than (<)
less than or equal to (≤)	more than (>)

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Null Hypothesis Definition and Examples

PM Images / Getty Images

Chemical Laws
Periodic Table
Projects & Experiments
Scientific Method
Biochemistry
Physical Chemistry
Medical Chemistry
Chemistry In Everyday Life
Famous Chemists
Activities for Kids
Abbreviations & Acronyms
Weather & Climate
Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
B.A., Physics and Mathematics, Hastings College

In a scientific experiment, the null hypothesis is the proposition that there is no effect or no relationship between phenomena or populations. If the null hypothesis is true, any observed difference in phenomena or populations would be due to sampling error (random chance) or experimental error. The null hypothesis is useful because it can be tested and found to be false, which then implies that there is a relationship between the observed data. It may be easier to think of it as a nullifiable hypothesis or one that the researcher seeks to nullify. The null hypothesis is also known as the H 0, or no-difference hypothesis.

The alternate hypothesis, H A or H 1 , proposes that observations are influenced by a non-random factor. In an experiment, the alternate hypothesis suggests that the experimental or independent variable has an effect on the dependent variable .

How to State a Null Hypothesis

There are two ways to state a null hypothesis. One is to state it as a declarative sentence, and the other is to present it as a mathematical statement.

For example, say a researcher suspects that exercise is correlated to weight loss, assuming diet remains unchanged. The average length of time to achieve a certain amount of weight loss is six weeks when a person works out five times a week. The researcher wants to test whether weight loss takes longer to occur if the number of workouts is reduced to three times a week.

The first step to writing the null hypothesis is to find the (alternate) hypothesis. In a word problem like this, you're looking for what you expect to be the outcome of the experiment. In this case, the hypothesis is "I expect weight loss to take longer than six weeks."

This can be written mathematically as: H 1 : μ > 6

In this example, μ is the average.

Now, the null hypothesis is what you expect if this hypothesis does not happen. In this case, if weight loss isn't achieved in greater than six weeks, then it must occur at a time equal to or less than six weeks. This can be written mathematically as:

H 0 : μ ≤ 6

The other way to state the null hypothesis is to make no assumption about the outcome of the experiment. In this case, the null hypothesis is simply that the treatment or change will have no effect on the outcome of the experiment. For this example, it would be that reducing the number of workouts would not affect the time needed to achieve weight loss:

H 0 : μ = 6

Null Hypothesis Examples

"Hyperactivity is unrelated to eating sugar " is an example of a null hypothesis. If the hypothesis is tested and found to be false, using statistics, then a connection between hyperactivity and sugar ingestion may be indicated. A significance test is the most common statistical test used to establish confidence in a null hypothesis.

Another example of a null hypothesis is "Plant growth rate is unaffected by the presence of cadmium in the soil ." A researcher could test the hypothesis by measuring the growth rate of plants grown in a medium lacking cadmium, compared with the growth rate of plants grown in mediums containing different amounts of cadmium. Disproving the null hypothesis would set the groundwork for further research into the effects of different concentrations of the element in soil.

Why Test a Null Hypothesis?

You may be wondering why you would want to test a hypothesis just to find it false. Why not just test an alternate hypothesis and find it true? The short answer is that it is part of the scientific method. In science, propositions are not explicitly "proven." Rather, science uses math to determine the probability that a statement is true or false. It turns out it's much easier to disprove a hypothesis than to positively prove one. Also, while the null hypothesis may be simply stated, there's a good chance the alternate hypothesis is incorrect.

For example, if your null hypothesis is that plant growth is unaffected by duration of sunlight, you could state the alternate hypothesis in several different ways. Some of these statements might be incorrect. You could say plants are harmed by more than 12 hours of sunlight or that plants need at least three hours of sunlight, etc. There are clear exceptions to those alternate hypotheses, so if you test the wrong plants, you could reach the wrong conclusion. The null hypothesis is a general statement that can be used to develop an alternate hypothesis, which may or may not be correct.

Kelvin Temperature Scale Definition
Independent Variable Definition and Examples
Theory Definition in Science
Hypothesis Definition (Science)
de Broglie Equation Definition
Law of Combining Volumes Definition
Chemical Definition
Pure Substance Definition in Chemistry
Acid Definition and Examples
Extensive Property Definition (Chemistry)
Radiation Definition and Examples
Valence Definition in Chemistry
Atomic Solid Definition
Weak Base Definition and Examples
Oxidation Definition and Example in Chemistry
Definition of Binary Compound

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

Hypothesis Testing: Uses, Steps & Example

By Jim Frost 4 Comments

What is Hypothesis Testing?

Hypothesis testing in statistics uses sample data to infer the properties of a whole population . These tests determine whether a random sample provides sufficient evidence to conclude an effect or relationship exists in the population. Researchers use them to help separate genuine population-level effects from false effects that random chance can create in samples. These methods are also known as significance testing.

For example, researchers are testing a new medication to see if it lowers blood pressure. They compare a group taking the drug to a control group taking a placebo. If their hypothesis test results are statistically significant, the medication’s effect of lowering blood pressure likely exists in the broader population, not just the sample studied.

Using Hypothesis Tests

A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement the sample data best supports. These two statements are called the null hypothesis and the alternative hypothesis . The following are typical examples:

Null Hypothesis : The effect does not exist in the population.
Alternative Hypothesis : The effect does exist in the population.

Hypothesis testing accounts for the inherent uncertainty of using a sample to draw conclusions about a population, which reduces the chances of false discoveries. These procedures determine whether the sample data are sufficiently inconsistent with the null hypothesis that you can reject it. If you can reject the null, your data favor the alternative statement that an effect exists in the population.

Statistical significance in hypothesis testing indicates that an effect you see in sample data also likely exists in the population after accounting for random sampling error , variability, and sample size. Your results are statistically significant when the p-value is less than your significance level or, equivalently, when your confidence interval excludes the null hypothesis value.

Conversely, non-significant results indicate that despite an apparent sample effect, you can’t be sure it exists in the population. It could be chance variation in the sample and not a genuine effect.

Learn more about Failing to Reject the Null .

5 Steps of Significance Testing

Hypothesis testing involves five key steps, each critical to validating a research hypothesis using statistical methods:

Formulate the Hypotheses : Write your research hypotheses as a null hypothesis (H 0 ) and an alternative hypothesis (H A ).
Data Collection : Gather data specifically aimed at testing the hypothesis.
Conduct A Test : Use a suitable statistical test to analyze your data.
Make a Decision : Based on the statistical test results, decide whether to reject the null hypothesis or fail to reject it.
Report the Results : Summarize and present the outcomes in your report’s results and discussion sections.

While the specifics of these steps can vary depending on the research context and the data type, the fundamental process of hypothesis testing remains consistent across different studies.

Let’s work through these steps in an example!

Hypothesis Testing Example

Researchers want to determine if a new educational program improves student performance on standardized tests. They randomly assign 30 students to a control group , which follows the standard curriculum, and another 30 students to a treatment group, which participates in the new educational program. After a semester, they compare the test scores of both groups.

Download the CSV data file to perform the hypothesis testing yourself: Hypothesis_Testing .

The researchers write their hypotheses. These statements apply to the population, so they use the mu (μ) symbol for the population mean parameter .

Null Hypothesis (H 0 ) : The population means of the test scores for the two groups are equal (μ 1 = μ 2 ).
Alternative Hypothesis (H A ) : The population means of the test scores for the two groups are unequal (μ 1 ≠ μ 2 ).

Choosing the correct hypothesis test depends on attributes such as data type and number of groups. Because they’re using continuous data and comparing two means, the researchers use a 2-sample t-test .

Here are the results.

Hypothesis testing results for the example.

The treatment group’s mean is 58.70, compared to the control group’s mean of 48.12. The mean difference is 10.67 points. Use the test’s p-value and significance level to determine whether this difference is likely a product of random fluctuation in the sample or a genuine population effect.

Because the p-value (0.000) is less than the standard significance level of 0.05, the results are statistically significant, and we can reject the null hypothesis. The sample data provides sufficient evidence to conclude that the new program’s effect exists in the population.

Limitations

Hypothesis testing improves your effectiveness in making data-driven decisions. However, it is not 100% accurate because random samples occasionally produce fluky results. Hypothesis tests have two types of errors, both relating to drawing incorrect conclusions.

Type I error: The test rejects a true null hypothesis—a false positive.
Type II error: The test fails to reject a false null hypothesis—a false negative.

Learn more about Type I and Type II Errors .

Our exploration of hypothesis testing using a practical example of an educational program reveals its powerful ability to guide decisions based on statistical evidence. Whether you’re a student, researcher, or professional, understanding and applying these procedures can open new doors to discovering insights and making informed decisions. Let this tool empower your analytical endeavors as you navigate through the vast seas of data.

Learn more about the Hypothesis Tests for Various Data Types .

Reader Interactions

June 10, 2024 at 10:51 am

Thank you, Jim, for another helpful article; timely too since I have started reading your new book on hypothesis testing and, now that we are at the end of the school year, my district is asking me to perform a number of evaluations on instructional programs. This is where my question/concern comes in. You mention that hypothesis testing is all about testing samples. However, I use all the students in my district when I make these comparisons. Since I am using the entire “population” in my evaluations (I don’t select a sample of third grade students, for example, but I use all 700 third graders), am I somehow misusing the tests? Or can I rest assured that my district’s student population is only a sample of the universal population of students?

June 10, 2024 at 1:50 pm

I hope you are finding the book helpful!

Yes, the purpose of hypothesis testing is to infer the properties of a population while accounting for random sampling error.

In your case, it comes down to how you want to use the results. Who do you want the results to apply to?

If you’re summarizing the sample, looking for trends and patterns, or evaluating those students and don’t plan to apply those results to other students, you don’t need hypothesis testing because there is no sampling error. They are the population and you can just use descriptive statistics. In this case, you’d only need to focus on the practical significance of the effect sizes.

On the other hand, if you want to apply the results from this group to other students, you’ll need hypothesis testing. However, there is the complicating issue of what population your sample of students represent. I’m sure your district has its own unique characteristics, demographics, etc. Your district’s students probably don’t adequately represent a universal population. At the very least, you’d need to recognize any special attributes of your district and how they could bias the results when trying to apply them outside the district. Or they might apply to similar districts in your region.

However, I’d imagine your 3rd graders probably adequately represent future classes of 3rd graders in your district. You need to be alert to changing demographics. At least in the short run I’d imagine they’d be representative of future classes.

Think about how these results will be used. Do they just apply to the students you measured? Then you don’t need hypothesis tests. However, if the results are being used to infer things about other students outside of the sample, you’ll need hypothesis testing along with considering how well your students represent the other students and how they differ.

I hope that helps!

June 10, 2024 at 3:21 pm

Thank you so much, Jim, for the suggestions in terms of what I need to think about and consider! You are always so clear in your explanations!!!!

June 10, 2024 at 3:22 pm

You’re very welcome! Best of luck with your evaluations!

Comments and Questions Cancel reply

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

Research Question	Null Hypothesis
Do teenagers use cell phones more than adults?	Teenagers and adults use cell phones the same amount.
Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil?	Tomato plants show no difference in growth rates when planted in compost rather than soil.
Does daily meditation decrease the incidence of depression?	Daily meditation does not decrease the incidence of depression.
Does daily exercise increase test performance?	There is no relationship between daily exercise time and test performance.
Does the new vaccine prevent infections?	The vaccine does not affect the infection rate.
Does flossing your teeth affect the number of cavities?	Flossing your teeth has no effect on the number of cavities.

When Do We Reject The Null Hypothesis?

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Probability and statistical significance in ab testing. Statistical significance in a b experiments

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.

Purpose of a Null Hypothesis

The primary purpose of the null hypothesis is to disprove an assumption.
Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.

Null Hypothesis Definition and Examples, How to State

What is the null hypothesis, how to state the null hypothesis, null hypothesis overview.

null hypothesis statistical testing example

Why is it Called the “Null”?

The word “null” in this context means that it’s a commonly accepted fact that researchers work to nullify . It doesn’t mean that the statement is null (i.e. amounts to nothing) itself! (Perhaps the term should be called the “nullifiable hypothesis” as that might cause less confusion).

Why Do I need to Test it? Why not just prove an alternate one?

The short answer is, as a scientist, you are required to ; It’s part of the scientific process. Science uses a battery of processes to prove or disprove theories, making sure than any new hypothesis has no flaws. Including both a null and an alternate hypothesis is one safeguard to ensure your research isn’t flawed. Not including the null hypothesis in your research is considered very bad practice by the scientific community. If you set out to prove an alternate hypothesis without considering it, you are likely setting yourself up for failure. At a minimum, your experiment will likely not be taken seriously.

Null hypothesis : H 0 : The world is flat.
Alternate hypothesis: The world is round.

Several scientists, including Copernicus , set out to disprove the null hypothesis. This eventually led to the rejection of the null and the acceptance of the alternate. Most people accepted it — the ones that didn’t created the Flat Earth Society !. What would have happened if Copernicus had not disproved the it and merely proved the alternate? No one would have listened to him. In order to change people’s thinking, he first had to prove that their thinking was wrong .

How to State the Null Hypothesis from a Word Problem

You’ll be asked to convert a word problem into a hypothesis statement in statistics that will include a null hypothesis and an alternate hypothesis . Breaking your problem into a few small steps makes these problems much easier to handle.

Step 2: Convert the hypothesis to math . Remember that the average is sometimes written as μ.

H 1 : μ > 8.2

Broken down into (somewhat) English, that’s H 1 (The hypothesis): μ (the average) > (is greater than) 8.2

Step 3: State what will happen if the hypothesis doesn’t come true. If the recovery time isn’t greater than 8.2 weeks, there are only two possibilities, that the recovery time is equal to 8.2 weeks or less than 8.2 weeks.

H 0 : μ ≤ 8.2

Broken down again into English, that’s H 0 (The null hypothesis): μ (the average) ≤ (is less than or equal to) 8.2

How to State the Null Hypothesis: Part Two

But what if the researcher doesn’t have any idea what will happen.

Example Problem: A researcher is studying the effects of radical exercise program on knee surgery patients. There is a good chance the therapy will improve recovery time, but there’s also the possibility it will make it worse. Average recovery times for knee surgery patients is 8.2 weeks.

Step 1: State what will happen if the experiment doesn’t make any difference. That’s the null hypothesis–that nothing will happen. In this experiment, if nothing happens, then the recovery time will stay at 8.2 weeks.

H 0 : μ = 8.2

Broken down into English, that’s H 0 (The null hypothesis): μ (the average) = (is equal to) 8.2

Step 2: Figure out the alternate hypothesis . The alternate hypothesis is the opposite of the null hypothesis. In other words, what happens if our experiment makes a difference?

H 1 : μ ≠ 8.2

In English again, that’s H 1 (The alternate hypothesis): μ (the average) ≠ (is not equal to) 8.2

That’s How to State the Null Hypothesis!

Check out our Youtube channel for more stats tips!

Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial. Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences , Wiley.

13.1 Understanding Null Hypothesis Testing

Learning objectives.

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of adults with clinical depression, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.

You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.

“Null Hypothesis” retrieved from http://imgs.xkcd.com/comics/null_hypothesis.png (CC-BY-NC 2.5)

Role of Sample Size and Relationship Strength

Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”



Sample Size	Weak	Medium	Strong
Small ( = 20)	No	No	= Maybe = Yes
Medium ( = 50)	No	Yes	Yes
Large ( = 100)	= Yes = No	Yes	Yes
Extra large ( = 500)	Yes	Yes	Yes

Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

“Conditional Risk” retrieved from http://imgs.xkcd.com/comics/conditional_risk.png (CC-BY-NC 2.5)

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Share This Book

Increase Font Size

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 13: Inferential Statistics

Understanding Null Hypothesis Testing

Learning Objectives

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favour of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Table 13.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant
Sample Size	Weak relationship	Medium-strength relationship	Strong relationship
Small ( = 20)	No	No	= Maybe = Yes
Medium ( = 50)	No	Yes	Yes
Large ( = 100)	= Yes = No	Yes	Yes
Extra large ( = 500)	Yes	Yes	Yes

Statistical Significance Versus Practical Significance

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.

Long Descriptions

“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]

“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]

Media Attributions

Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Values in a population that correspond to variables measured in a study.

The random variability in a statistic from sample to sample.

A formal approach to deciding between two interpretations of a statistical relationship in a sample.

The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.

The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.

When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.

The probability that, if the null hypothesis were true, the result found in the sample would occur.

How low the p value must be before the sample result is considered unlikely in null hypothesis testing.

When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.

Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base
Choosing the Right Statistical Test | Types & Examples

Choosing the Right Statistical Test | Types & Examples

Published on January 28, 2020 by Rebecca Bevans . Revised on June 22, 2023.

Statistical tests are used in hypothesis testing . They can be used to:

determine whether a predictor variable has a statistically significant relationship with an outcome variable.
estimate the difference between two or more groups.

Statistical tests assume a null hypothesis of no relationship or no difference between groups. Then they determine whether the observed data fall outside of the range of values predicted by the null hypothesis.

If you already know what types of variables you’re dealing with, you can use the flowchart to choose the right statistical test for your data.

Statistical tests flowchart

What does a statistical test do, when to perform a statistical test, choosing a parametric test: regression, comparison, or correlation, choosing a nonparametric test, flowchart: choosing a statistical test, other interesting articles, frequently asked questions about statistical tests.

Statistical tests work by calculating a test statistic – a number that describes how much the relationship between variables in your test differs from the null hypothesis of no relationship.

It then calculates a p value (probability value). The p -value estimates how likely it is that you would see the difference described by the test statistic if the null hypothesis of no relationship were true.

If the value of the test statistic is more extreme than the statistic calculated from the null hypothesis, then you can infer a statistically significant relationship between the predictor and outcome variables.

If the value of the test statistic is less extreme than the one calculated from the null hypothesis, then you can infer no statistically significant relationship between the predictor and outcome variables.

Prevent plagiarism. Run a free check.

You can perform statistical tests on data that have been collected in a statistically valid manner – either through an experiment , or through observations made using probability sampling methods .

For a statistical test to be valid , your sample size needs to be large enough to approximate the true distribution of the population being studied.

To determine which statistical test to use, you need to know:

whether your data meets certain assumptions.
the types of variables that you’re dealing with.

Statistical assumptions

Statistical tests make some common assumptions about the data they are testing:

Independence of observations (a.k.a. no autocorrelation): The observations/variables you include in your test are not related (for example, multiple measurements of a single test subject are not independent, while measurements of multiple different test subjects are independent).
Homogeneity of variance : the variance within each group being compared is similar among all groups. If one group has much more variation than others, it will limit the test’s effectiveness.
Normality of data : the data follows a normal distribution (a.k.a. a bell curve). This assumption applies only to quantitative data .

If your data do not meet the assumptions of normality or homogeneity of variance, you may be able to perform a nonparametric statistical test , which allows you to make comparisons without any assumptions about the data distribution.

If your data do not meet the assumption of independence of observations, you may be able to use a test that accounts for structure in your data (repeated-measures tests or tests that include blocking variables).

Types of variables

The types of variables you have usually determine what type of statistical test you can use.

Quantitative variables represent amounts of things (e.g. the number of trees in a forest). Types of quantitative variables include:

Continuous (aka ratio variables): represent measures and can usually be divided into units smaller than one (e.g. 0.75 grams).
Discrete (aka integer variables): represent counts and usually can’t be divided into units smaller than one (e.g. 1 tree).

Categorical variables represent groupings of things (e.g. the different tree species in a forest). Types of categorical variables include:

Ordinal : represent data with an order (e.g. rankings).
Nominal : represent group names (e.g. brands or species names).
Binary : represent data with a yes/no or 1/0 outcome (e.g. win or lose).

Choose the test that fits the types of predictor and outcome variables you have collected (if you are doing an experiment , these are the independent and dependent variables ). Consult the tables below to see which test best matches your variables.

Parametric tests usually have stricter requirements than nonparametric tests, and are able to make stronger inferences from the data. They can only be conducted with data that adheres to the common assumptions of statistical tests.

The most common types of parametric test include regression tests, comparison tests, and correlation tests.

Regression tests

Regression tests look for cause-and-effect relationships . They can be used to estimate the effect of one or more continuous variables on another variable.

	Predictor variable	Outcome variable	Research question example
			What is the effect of income on longevity?
			What is the effect of income and minutes of exercise per day on longevity?
Logistic regression			What is the effect of drug dosage on the survival of a test subject?

Comparison tests

Comparison tests look for differences among group means . They can be used to test the effect of a categorical variable on the mean value of some other characteristic.

T-tests are used when comparing the means of precisely two groups (e.g., the average heights of men and women). ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults).

	Predictor variable	Outcome variable	Research question example
Paired t-test			What is the effect of two different test prep programs on the average exam scores for students from the same class?
Independent t-test			What is the difference in average exam scores for students from two different schools?
ANOVA			What is the difference in average pain levels among post-surgical patients given three different painkillers?
MANOVA			What is the effect of flower species on petal length, petal width, and stem length?

Correlation tests

Correlation tests check whether variables are related without hypothesizing a cause-and-effect relationship.

These can be used to test whether two variables you want to use in (for example) a multiple regression test are autocorrelated.

	Variables	Research question example
Pearson’s		How are latitude and temperature related?

Non-parametric tests don’t make as many assumptions about the data, and are useful when one or more of the common statistical assumptions are violated. However, the inferences they make aren’t as strong as with parametric tests.

	Predictor variable	Outcome variable	Use in place of…
Spearman’s
			Pearson’s
Sign test			One-sample -test
Kruskal–Wallis			ANOVA
ANOSIM			MANOVA
Wilcoxon Rank-Sum test			Independent t-test
Wilcoxon Signed-rank test			Paired t-test

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

This flowchart helps you choose among parametric tests. For nonparametric alternatives, check the table above.

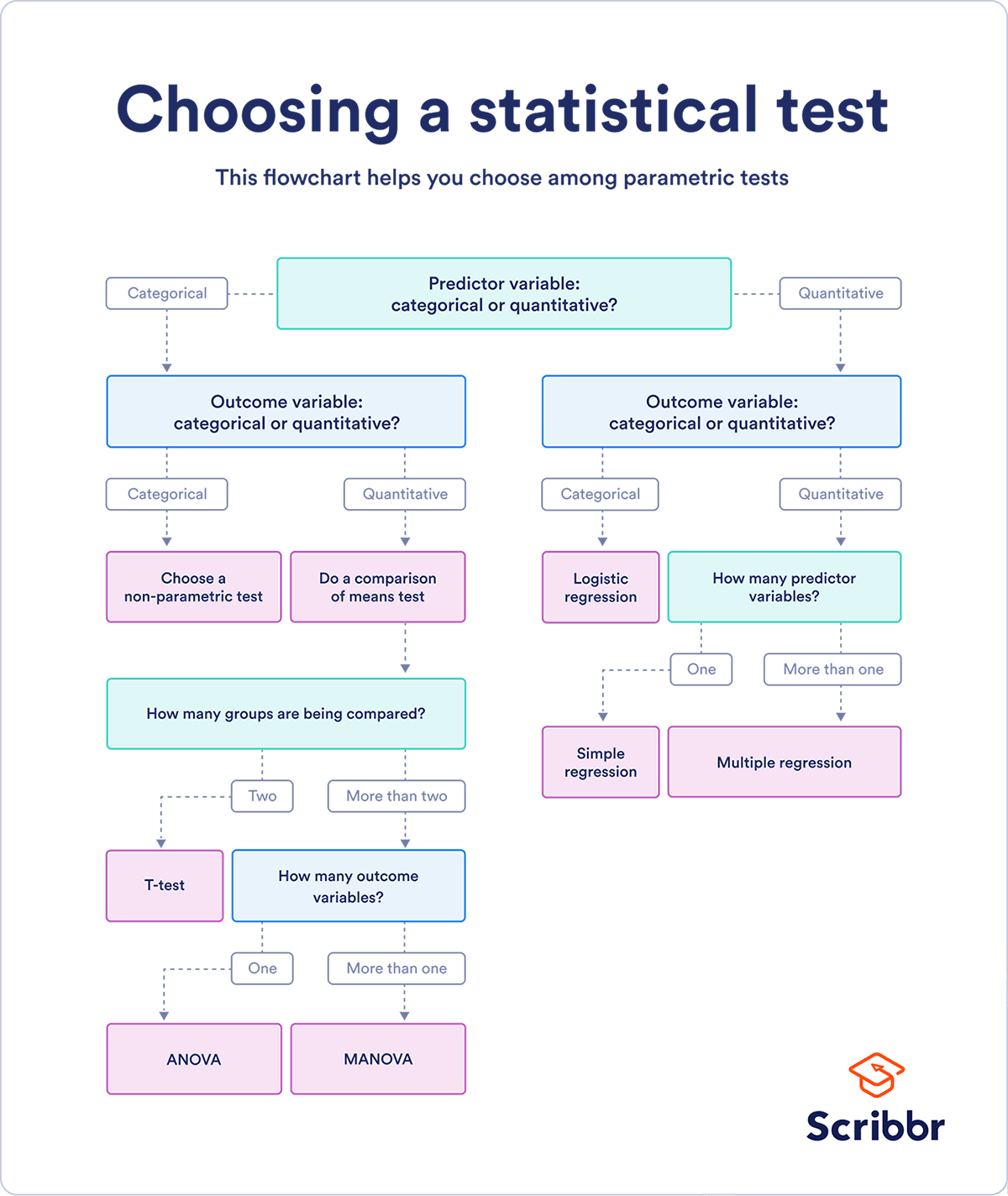
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient
Null hypothesis

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Statistical tests commonly assume that:

the data are normally distributed
the groups that are being compared have similar variance
the data are independent

If your data does not meet these assumptions you might still be able to use a nonparametric statistical test , which have fewer requirements but also make weaker inferences.

A test statistic is a number calculated by a statistical test . It describes how far your observed data is from the null hypothesis of no relationship between variables or no difference among sample groups.

The test statistic tells you how different two or more groups are from the overall population mean , or how different a linear slope is from the slope predicted by a null hypothesis . Different test statistics are used in different statistical tests.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).

Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).

You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .

Discrete and continuous variables are two types of quantitative variables :

Discrete variables represent counts (e.g. the number of objects in a collection).
Continuous variables represent measurable amounts (e.g. water volume or weight).

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Choosing the Right Statistical Test | Types & Examples. Scribbr. Retrieved September 27, 2024, from https://www.scribbr.com/statistics/statistical-tests/

Is this article helpful?

Rebecca Bevans

Other students also liked, hypothesis testing | a step-by-step guide with easy examples, test statistics | definition, interpretation, and examples, normal distribution | examples, formulas, & uses, what is your plagiarism score.

A Beginner's Guide to Hypothesis Testing: Key Concepts and Applications

September 27, 2024

In our everyday lives, we often encounter statements and claims that we can't instantly verify.

Have you ever questioned how to determine which statements are factual or validate them with certainty?

Fortunately, there's a systematic way to find answers: Hypothesis Testing.

Hypothesis Testing is a fundamental concept in analytics and statistics, yet it remains a mystery to many. This method helps us understand and validate data and supports decision-making in various fields.

Are you curious about how it works and why it's so crucial?

Let's understand the hypothesis testing basics and explore its applications together.

What is hypothesis testing in statistics?

Hypothesis evaluation is a statistical method used to determine whether there is enough evidence in a sample of data to support a particular assumption.

A statistical hypothesis test generally involves calculating a test statistic. The decision is then made by either comparing the test statistic to a crucial value or assessing the p-value derived from the test statistic.

The P-value in Hypothesis Testing

P-value helps determine whether to accept or reject the null hypothesis (H₀) during hypothesis testing.

Two types of errors in this process are:

Type I error (α):

This happens when the null hypothesis is incorrectly rejected, meaning we think there's an effect or difference when there isn't.

It is denoted by α (significance level).

Type II error (β)

This occurs when the null hypothesis gets incorrectly accepted, meaning we fail to detect an effect or difference that exists.

It is denoted by β (power level).

Type I error: Rejecting something that's true.
Type II error: Accepting something that's false.

Here's a simplified breakdown of the key components of hypothesis testing :

Null Hypothesis (H₀): The default assumption that there's no significant effect or difference
Alternative Hypothesis (H₁): The statement that challenges the null hypothesis, suggesting a significant effect
P-Value : This tells you how likely it is that your results happened by chance.
Significance Level (α): Typically set at 0.05, this is the threshold used to conclude whether to reject the null hypothesis.

This process is often used in financial analysis to test the effectiveness of trading strategies, assess portfolio performance, or predict market trends.

Statistical Hypothesis Testing for Beginners: A Step-by-Step Guide

Applying hypothesis testing in finance requires a clear understanding of the steps involved.

Here's a practical approach for beginners:

STEP 1: Define the Hypothesis

Start by formulating your null and alternative hypotheses. For example, you might hypothesise that a certain stock's returns outperform the market average.

STEP 2: Collect Data

Gather relevant financial data from reliable sources, ensuring that your sample size is appropriate to draw meaningful conclusions.

STEP 3: Choose the Right Test

Select a one-tailed or two-tailed test depending on the data type and your hypothesis. Two-tailed tests are commonly used for financial analysis to assess whether a parameter differs in either direction.

STEP 4: Calculate the Test Statistic

Use statistical software or a financial calculator to compute your test statistic and compare it to the critical value.

STEP 5: Interpret the Results

Based on the p-value, decide whether to reject or fail to reject the null hypothesis. If the p-value is below the significance level, it indicates that the null hypothesis is unlikely, and you may accept the alternative hypothesis.

Here's a quick reference table to help with your decisions:

Test Type	Null Hypothesis	Alternative Hypothesis	Use Case in Finance
	No effect or no gain	A positive or negative impact	Testing a specific directional claim about stock returns
	No difference	Any significant difference	Comparing performance between two portfolios

Real-Life Applications of Hypothesis Testing in Finance

The concept of hypothesis testing basics might sound theoretical, but its real-world applications are vast in the financial sector.

Here's how professionals use it:

Investment Portfolio Performance : Analysts often use statistical hypothesis testing for beginners to determine whether one investment portfolio performs better than another.
Risk Assessment: Statistical testing helps evaluate market risk by testing assumptions about asset price movements and volatility.
Forecasting Market Trends : Predicting future market trends using past data can be tricky, but research testing allows professionals to make more informed predictions by validating their assumptions.

Common Pitfalls to Avoid in Hypothesis Testing

Even seasoned professionals sometimes need to correct their theory testing analysis.

Here are some common mistakes you'll want to avoid:

Misinterpreting P-Values

A common misunderstanding is that a low p-value proves that the alternative hypothesis is correct. It just means there's strong evidence against the null hypothesis.

Ignoring Sample Size

Small sample sizes can also lead to misleading results, so ensuring that your data set is large enough to provide reliable insights is crucial.

Overfitting the Model

This happens when you tailor your hypothesis too closely to the sample data, resulting in a model that only holds up under different conditions.

By being aware of these pitfalls, you'll be better positioned to conduct accurate hypothesis tests in any financial scenario.

Lead The World of Finance with Imarticus Learning

Mastering hypothesis testing is crucial for making informed financial decisions and validating assumptions. Consider the exceptional CFA course at Imarticus Learning as you enhance your analytical skills.

Achieve a prestigious qualification in investment management and thrive in a competitive industry. Imarticus, a leading learning partner approved by the CFA Institute, offers the best CFA course . Benefit from Comprehensive Learning with top-tier materials from Kaplan Schweser, including books, study notes, and mock exams.

Ready to elevate your finance career?

Enrol now and unlock your potential with Imarticus Learning!

Q: What is hypothesis testing in finance?

A: This is a statistical method used in finance to validate assumptions or hypotheses about financial data, such as testing the performance of investment strategies.

Q: What are the types of hypothesis testing?

A: The two primary types are one-tailed and two-tailed tests. You can use one-tailed tests to assess a specific direction of effect, while you can use two-tailed tests to determine if there is any significant difference, regardless of the direction.

Q: What is a p-value in hypothesis testing?

A: A p-value indicates the probability that your observed results occurred by chance. A lower p-value suggests stronger evidence against the null hypothesis.

Q: Why is sample size important in hypothesis testing?

A: A larger sample size increases the reliability of results, reducing the risk of errors and providing more accurate conclusions in hypothesis testing.

Share This Post

Subscribe to our newsletter, get updates and learn from the best, more to explore.

Your Ultimate Guide to Becoming a Chartered Financial Analyst

Your ultimate guide to acca exam dates: stay ahead of the curve, our programs.

Certified Investment Banking Operations Professional

Chief Financial Officer Programme

Global Senior Leadership Programme Specialisation: Chief Finance Officer

Advanced Management Programme In Financial Services And Capital Markets

Senior Leadership Programme In Fintech

Chartered Financial Analyst (CFA)

Certified Management Accountant

Certified Public Accountant

Do you want to boost your career, drop us a message and keep in touch.

Keep In Touch

Introduction to Hypothesis Testing

NC State University ST 511 - Fall 2024

– Keep up with Slack

– AE Solutions Posted

– Quiz 2 Solutions Posted

– HW-2 Posted Today ~ 5:00 (due Monday 23rd)

– HW-1 Solutions (today; grades soon)

Announcements

Quiz 3 - Question 3

The Central Limit Theorem states that we always need to have at least a sample size of at least n = 30 for the sampling distribution of a sample statistic to be approximately normal.

\(\geq 30\) vs \(> 30\)

The literature is sloppy (and apparently so am I)

Both is fine. I’m going to be more consistent with \(> 30\)

Warm Up Question

Notation check

\(\hat{p}\)

\(\bar{x}\)

\(\hat{p}\) - sample proportion

\(\mu\) - population mean

\(\bar{x}\) - sample mean

\(\pi\) - population proportion

Suppose you are a researcher interested in studying food habits for NC State students. You take a random sample of 100 students, and are interested in if they had Howling Cow ice creme with their dinner or now. We observed 37 students have ice creme, and 63 students not have ice creme.

– What is our random variable (X)?

– What type of variable are we working with?

Suppose you are a researcher interested in studying food habits for NC State students. You take a random sample of 100 students, and are interested in if they have Howling Cow ice creme with their dinner or now. We observed 37 students have ice creme, and 63 students not have ice creme.

We know that the Central Limit Theorem works with means (under certain conditions). Can X be represented as a mean?

\[ X = \begin{cases} 1 & \text{if yes}\\ 0 & \text{if no} \end{cases} \]

1, 0, 1, 1, 0, 1, 0, 1, …..

The mean of a binary outcome is just the sample proportion

Do Students Eat Howling Cow?

– Set up your null and alternative hypothesis

– Collect data

– Quantify evidence

– Articulate your results

Suppose the Howling Cow company claims that 50% of NC State students eat Howling Cow at dinner. We think that less than 50% of students eat Howling Cow at dinner.

\(H_o\) : - The assumption that is made

\(H_a\) - The research question

\(H_o\) : \(\pi\) = 0.5

\(H_a\) \(\pi\) < 0.5

Collect Data

You take a random sample of 100 students, and are interested in if they have Howling Cow ice creme with their dinner or now. We observed 37 students have ice creme, and 63 students not have ice creme.

What is the proper notation for our sample statistic?

You take a random sample of 100 students, and are interested in if they had Howling Cow ice creme with their dinner or now. We observed 37 students have ice creme, and 63 students not have ice creme.

\(\hat{p}\) = \(\frac{37}{100}\)

Null Distribution

A null distribution is a sampling distribution under the assumption of the null hypothesis. It describes how that statistic would vary from sample to sample, if the null hypothesis were true .

We can use theory or simulation techniques to model this distribution if our assumptions hold!

Theory Based Methods

Assumptions for single proportion

– Independence (this never goes away)

– Sample size (a little different than with means)

Sample Size Assumption

– Need to think about the number of successes + failures

– Need to think about creating a sampling distribution under the assumption of the null hypothesis

– \(\pi = 0.5\)

So we ask ourselves, if the null is true, how many successes and failures would we expect to see out of our sample size of 100?

Success = 0.5

100*.5 = 50

Failure = 0.5

Estimating the sampling distribution

The null value will be the center

We can estimate the standard error of the null sampling distribution as so:

\[ \sqrt{\frac{\pi_o * (1-\pi_o)}{n}} \]

What this looks like

Standardize

Often, with theory-based methods, we use a standardized statistic. A standardized statistic is computed by subtracting the mean of the null distribution from the original statistic and dividing by the standard error

\[ \text{statistic} = \frac{statistc - null}{SE(null)} \]

– The standardized statistic has a nice definition

– Helps compare across multiple studies with different units

Standardized test statistc

\[ Z = \frac{.37 - .5}{.05} = -2.6 \]

Interpretation - Interpreting this value, we can say that our sample proportion of 0.37 is 2.6 standard errors below the null value of 0.50.

The reason you can use a z-test with proportions is because the standard deviation of a proportion is a function of the proportion itself. With proportions, we assume the standard deviation is known exactly.

Under an assumption of some null hypothesis, would you expect to observe this statistic?

Probably not! Let’s quantify that thinking

A p-value is the probability of observing our sample statistic , or something more extreme given our null hypothesis is true

Let’s fill in the bold with our context!

A p-value is the probability of observing .37 , or something smaller given the true proportion of all NC State students that eat Howling Cow ice creme at dinner is 50%

pnorm() is used to calculate probabilities from a Normal distribution

– quantile (z-statistic of -2.6)

– lower.tail = [TRUE/FALSE]

\(\alpha\) (also called significance level), acts as a “cut-off” for how much evidence we need to reject the null hypothesis.

– In practice, this value is the % of times we make the incorrect decision

– This is decided before the study

– Typically 0.1, 0.05, or 0.01

We will use 0.05 for our study.

Let’s write up our results!

– Decision: Reject / Fail to reject our null hypothesis

– Conclusion: Weak / Strong evidence to conclude our alternative hypothesis

– Interpretation: Use the definition

Theory vs Simulation

The null distribution can be estimated through simulation (simulation-based methods), or can be modeled by a mathematical function (theory-based methods)

Let’s now talk about simulation (and practice with it in R)

– Simulation studies started to become popular as technology advanced

– Still need an independence assumption

– Less strict sample size assumption (no exact cut-off values)

Bumba vs Kiki

🔗 class website

School Guide
Mathematics
Number System and Arithmetic
Trigonometry
Probability
Mensuration
Maths Formulas
Integration Formulas
Differentiation Formulas
Trigonometry Formulas
Algebra Formulas
Mensuration Formula
Statistics Formulas
Trigonometric Table

Null Hypothesis

Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.

In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.

Table of Content

What is Null Hypothesis?

Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis – practice problems.

Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply “null,” it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.

Null Hypothesis Meaning

Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.

The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.

Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.

The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.

Mean Comparison (Two-sample t-test)

H 0 : μ 1 = μ 2

This asserts that there is no significant difference between the means of two populations or groups.

Proportion Comparison

H 0 : p 1 − p 2 = 0

This suggests no significant difference in proportions between two populations or conditions.

Equality in Variance (F-test in ANOVA)

H 0 : σ 1 = σ 2

This states that there’s no significant difference in variances between groups or populations.

Independence (Chi-square Test of Independence):

H 0 : Variables are independent

This asserts that there’s no association or relationship between categorical variables.

Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.

Equality Null Hypothesis (Simple Null Hypothesis)

The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.

Non-Inferiority Null Hypothesis

In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.

Superiority Null Hypothesis

The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.

Independence Null Hypothesis

In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.

Homogeneity Null Hypothesis

In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there’s no difference in population means across different groups.

Medicine: Null Hypothesis: “No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo.”
Education: Null Hypothesis: “There’s no significant variation in test scores between students using a new teaching method and those using traditional teaching.”
Economics: Null Hypothesis: “There’s no significant change in consumer spending pre- and post-implementation of a new taxation policy.”
Environmental Science: Null Hypothesis: “There’s no substantial difference in pollution levels before and after a water treatment plant’s establishment.”

The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.

In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.

The null hypothesis is usually formulated to be tested against an alternative hypothesis (H 1 or H \alpha ) which suggests that there is an effect, difference or relationship present in the population.

Null Hypothesis Rejection

Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.

When is Null Hypothesis Rejected?

The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher’s claim or the hypothesis they seek to support.

The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.

In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.

Difference Between Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher’s intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.


Criteria	Null Hypothesis	Alternative Hypothesis
Definition	Assumes no effect or difference	Asserts a specific effect or difference
Symbol	H	H (or Ha)
Formulation	States equality or absence of parameter	States a specific value or relationship
Testing Outcome	Rejected if evidence of a significant effect	Accepted if evidence supports the hypothesis

Let’s envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:

Null Hypothesis (H 0 ): “The new medication does not produce a significant effect in reducing blood pressure levels among patients.”

Alternative Hypothesis (H 1 or Ha): “The new medication yields a significant effect in reducing blood pressure levels among patients.”

The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication’s administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.

Summary – Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher’s hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.

FAQs on Null Hypothesis

What does null hypothesis stands for.

The null hypothesis, denoted as H 0 , is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.

How to Form a Null Hypothesis?

A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.

When Do we reject the Null Hypothesis?

In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.

What is a Null Hypothesis in Research?

In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.

What Are Alternative and Null Hypotheses?

The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.

What Does it Mean to Reject the Null Hypothesis?

Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.

How to Find Null Hypothesis?

Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.

How is Null Hypothesis denoted?

The null hypothesis is commonly symbolized as H 0 in statistical notation.

What is the Purpose of the Null hypothesis in Statistical Analysis?

The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there’s enough evidence to reject it in favor of an alternative hypothesis.

What happens if we Reject the Null hypothesis?

Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.

What are Test for Null Hypothesis?

Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.

Please Login to comment...

How to Watch NFL on NFL+ in 2024: A Complete Guide
Best Smartwatches in 2024: Top Picks for Every Need
Top Budgeting Apps in 2024
10 Best Parental Control App in 2024
GeeksforGeeks Practice - Leading Online Coding Platform

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Estimation and testing of expectile regression with efficient subsampling for massive data

Regular Article
Published: 28 September 2024

Cite this article

Baolin Chen 1 ,
Shanshan Song ORCID: orcid.org/0000-0002-0892-3032 2 &
Yong Zhou 3

Subsampling strategy plays a crucial role in statistical inference for massive data owing to its computing and storage superiority. The parameter estimation and hypothesis testing of expectile regression for massive data is of concern. This paper offers an alternative to the traditional asymmetric least square (ALS) estimator via smooth approximation of loss function. Then, an efficient subsampling algorithm based on Newton’s iteration is proposed. We prove consistency and asymptotic normality and provide the optimal subsampling probability and the proper order of smoothing parameter. We also apply the subsampling strategy for hypothesis testing, where the proposed test statistics have bigger power, compared with the test statistic based on the simple random subsampling. Simulation and two real data examples demonstrate the effectiveness of the proposed subsampling estimation and testing methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save.

Get 10 units per month
Download Article/Chapter or eBook
1 Unit = 1 Article or 1 Chapter
Cancel anytime

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Deterministic subsampling for logistic regression with massive data

Poisson subsampling-based estimation for growing-dimensional expectile regression in massive data

Entropy-Based Subsampling Methods for Big Data

Ai M, Wang F, Yu J, Zhang H (2020) Optimal subsampling for large-scale quantile regression. J Complex 62:101512

Article MathSciNet Google Scholar

Barry A, Oualkacha K, Charpentier A (2021) A new GEE method to account for heteroscedasticity using asymmetric least-square regressions. J Appl Stat 49(14):3564–3590

Chen X, Liu W, Zhang Y (2019) Quantile regression under memory constraint. Ann Stat 47(6):3244–3273

Chen X, Xie M (2014) A split-and-conquer approach for analysis of extraordinarily large data. Stat Sin 24:1655–1684

MathSciNet Google Scholar

Daouia A, Girard S, Stupfler G (2018) Estimation of tail risk based on extreme expectiles. J R Stat Soc Ser B 80(2):263–292

Drineas P, Mahoney MW, Muthukrishnan S (2006) Sampling algorithms for l2 regression and applications. In: Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithm. Society for Industrial and Applied Mathematics, Philadelphia, PA, pp 1127–1136

Falk M (1999) A simple approach to the generation of uniformly distributed random variables with prescribed correlations. Commun. Stat. Simul. Comput 28:785–791

Fithian W, Hastie T (2014) Local case-control sampling: efficient subsampling in imbalanced data sets. Ann Stat 42:1693–1724

Fonollosa J, Sheik S, Huerta R, Marco S (2015) Reservoir computing compensates slow response of chemosensor arrays exposed to fast varying gas concentrations in continuous monitoring. Sens Actuators B 215:618–629

Article Google Scholar

Guo M, Härdle W (2013) Simultaneous confidence bands for expectile functions. AStA 96(4):517–541

Kaya H, Tüfekci P, Gürgen F (2012) Local and Global Learning Methods for Predicting Power of a Combined Gas & Steam Turbine. In: Proceedings of the International Conference on Emerging Trends in Computer and Electronics Engineering, pp 13–18

Kleiner A, Talwalkar A, Sarkar P, Jordan MI (2014) A scalable bootstrap for massive data. J R Stat Soc Ser B 76:795–816

Koenker R, Bassett Jr G (1978) Regression quantiles. Econometrica: Journal of the Econometric Society, 33–50

Kuan C, Yeh J, Hsu Y (2009) Assessing value at risk with care, the conditional autoregressive expectile models. J Econ 150(2):261–270

Li Q, Cheng G, Fan J, Wang Y (2018) Embracing the blessing of dimensionality in factor models. J Am Stat Assoc 113(521):380–389

Lin N, Xi R (2011) Aggregated estimating equation estimation. Stat Interface 4(1):73–83

Ma P, Mahoney M, Yu B (2014) A statistical perspective on algorithmic leveraging. In: Proceedings of the 31st International Conference on Machine Learning (ICML-14), pp 91–99

Ma P, Mahoney M, Yu B (2015) A statistical perspective on algorithmic leveraging. J Mach Learn Res 16:861–911

Newey WK, Powell JL (1987) Asymmetric least squares estimation and testing. Econometrica 55:819–847

Politis DN, Romano JP, Wolf M (1999) Subsampling. Springer, New York

Book Google Scholar

Politis DN, Romano JP, Wolf M (2001) On the asymptotic theory of subsampling. Stat Sin 11:1105–1124

Schifano ED, Wu J, Wang C, Yan J, Chen MH (2016) Online updating of statistical inference in the big data setting. Technometrics 58(3):393–403

Schnabel S, Eilers P (2009) Optimal expectile smoothing. Comput Stat Data Anal 53(12):4168–4177

Sengupta S, Volgushev S, Shao X (2016) A subsampled double bootstrap for massive data. J Am Stat Assoc 111(515):1222–1232

Sobotka F, Kauermann G, Schulze Waltrup L, Kneib T (2013) On confidence intervals for semiparametric expectile regression. Stat Comput 23(2):135–148

Sobotka F, Radice R, Marra G, Kneib T (2013) Estimating the relationship between women’s education and fertility in Botswana by using an instrumental variable approach to semiparametric expectile regression. J R Stat Soc Ser C 62(1):25–45

Song S, Lin Y, Zhou Y (2021) Linear expectile regression under massive data. Fundam Res 1(5):574–585

Tang L, Zhou L, Song P (2020) Distributed simultaneous inference in generalized linear models via confidence distribution. J Multivar Anal 176:104567

Volgushev S, Chao S, Cheng G (2017) Distribution inference for quantile regression processes. Ann Stat 43(3):1634–1662

Google Scholar

Wang B, Fang Y, Lian H, Liang H (2017) Additive partially linear models for massive heterogeneous data. Electron J Stat 13:391–431

Wang C, Chen M, Schifano E, Wu J, Yan J (2016) Statistical methods and computing for big data. Stat Interface 9:399–414

Wang H (2019) More efficient estimation for logistic regression with optimal subsamples. J Mach Learn Res 20(132):1–59

Wang HY, Zhu R, Ma P (2018) Optimal subsampling for large sample logistic regression. J Am Stat Assoc 113(522):829–844

Wang H, Yang M, Stufken J (2019) Information-based optimal subdata selection for big data linear regression. J Am Stat Assoc 114:393–405

Wang H, Ma Y (2021) Optimal subsampling for quantile regression in big data. Biometrika 108:99–112

Xie S, Zhou Y, Wan AT (2014) A varying-coefficient expectile model for estimating value at risk. J Bus Econ Stat 32(4):576–592

Download references

Acknowledgements

Zhou’s work was supported by the State Key Program of National Natural Science Foundation of China (71931004) and National Natural Science Foundation of China (92046005) and the National Key R &D Program of China (2021YFA1000100, 2021YFA1000101).

Author information

Authors and affiliations.

School of Statistics, Capital University of Business and Economics, Beijing, 100070, China

Baolin Chen

School of Mathematical Sciences, Tongji University, Shanghai, 200092, China

Shanshan Song

Key Laboratory of Advanced Theory and Application in Statistics and Data Science, MOE, and Academy of Statistics and Interdisciplinary Sciences and School of Statistics, East China Normal University, Shanghai, 200062, China

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shanshan Song .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Chen, B., Song, S. & Zhou, Y. Estimation and testing of expectile regression with efficient subsampling for massive data. Stat Papers (2024). https://doi.org/10.1007/s00362-024-01571-z

Download citation

Received : 12 November 2022

Revised : 12 March 2024

Published : 28 September 2024

DOI : https://doi.org/10.1007/s00362-024-01571-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Asymmetric least square (ALS) Estimator
Subsampling strategy
Newton’s iteration
Kernel smoothing
Find a journal
Publish with us
Track your research

IMAGES

15 Null Hypothesis Examples (2024)
Null Hypothesis Significance Testing Overview
Null Hypothesis Testing
PPT
Hypothesis Testing Solved Examples(Questions and Solutions)
Null Hypothesis

VIDEO

Writing the Null and Alternate Hypothesis in Statistics
Which of the following captures the idea of null hypothesis statistical testing (NHST) as used
8b. Hypothesis Testing
Hypothsis Testing in Statistics Part 2 Steps to Solving a Problem
The Similarity Between Statistical Hypothesis Testing and the Judiciary System
Hypothesis Testing: the null and alternative hypotheses

COMMENTS

Null Hypothesis: Definition, Rejecting & Examples
It is one of two mutually exclusive hypotheses about a population in a hypothesis test. When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant. Statisticians often denote the null hypothesis as H 0 or H A. Null Hypothesis H0: No effect exists in the population.
Null & Alternative Hypotheses
The null hypothesis (H0) answers "No, there's no effect in the population.". The alternative hypothesis (Ha) answers "Yes, there is an effect in the population.". The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
Hypothesis Testing
There are 5 main steps in hypothesis testing: State your research hypothesis as a null hypothesis and alternate hypothesis (H o) and (H a or H 1). Collect data in a way designed to test the hypothesis. Perform an appropriate statistical test. Decide whether to reject or fail to reject your null hypothesis. Present the findings in your results ...
Null and Alternative Hypotheses
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (HA): There's an effect in the population. The effect is usually the effect of the independent variable on the dependent ...
How to Write a Null Hypothesis (5 Examples)
Example 1: Weight of Turtles. A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles. Here is how to write the null and alternative hypotheses for this scenario: H0: μ = 300 (the true mean weight is equal to ...
How to Formulate a Null Hypothesis (With Examples)
To distinguish it from other hypotheses, the null hypothesis is written as H 0 (which is read as "H-nought," "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the ...
16.3: The Process of Null Hypothesis Testing
16.3.5 Step 5: Determine the probability of the data under the null hypothesis. This is the step where NHST starts to violate our intuition - rather than determining the likelihood that the null hypothesis is true given the data, we instead determine the likelihood of the data under the null hypothesis - because we started out by assuming that the null hypothesis is true!
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Null Hypothesis Definition and Examples
Null Hypothesis Examples. "Hyperactivity is unrelated to eating sugar " is an example of a null hypothesis. If the hypothesis is tested and found to be false, using statistics, then a connection between hyperactivity and sugar ingestion may be indicated. A significance test is the most common statistical test used to establish confidence in a ...
9.1: Null and Alternative Hypotheses
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
Hypothesis Testing: Uses, Steps & Example
Hypothesis testing involves five key steps, each critical to validating a research hypothesis using statistical methods: Formulate the Hypotheses: Write your research hypotheses as a null hypothesis (H 0) and an alternative hypothesis (H A). Data Collection: Gather data specifically aimed at testing the hypothesis.
What Is The Null Hypothesis & When To Reject It
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis. The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.
Null Hypothesis Definition and Examples, How to State
Step 1: Figure out the hypothesis from the problem. The hypothesis is usually hidden in a word problem, and is sometimes a statement of what you expect to happen in the experiment. The hypothesis in the above question is "I expect the average recovery period to be greater than 8.2 weeks.". Step 2: Convert the hypothesis to math.
13.1 Understanding Null Hypothesis Testing
The Logic of Null Hypothesis Testing. Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as "H-naught"). This is the idea that there is no relationship in the population and that the ...
S.3.3 Hypothesis Testing Examples
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t* were less than -1.6939 (determined using statistical software or a t-table):s-3-3. Since the biologist's test statistic, t* = -4.60, is less than -1.6939, the biologist rejects the null hypothesis.
Understanding Null Hypothesis Testing
Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance. The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct ...
1.2
Step 7: Based on Steps 5 and 6, draw a conclusion about H 0. If F calculated is larger than F α, then you are in the rejection region and you can reject the null hypothesis with (1 − α) level of confidence. Note that modern statistical software condenses Steps 6 and 7 by providing a p -value. The p -value here is the probability of getting ...
Choosing the Right Statistical Test
What does a statistical test do? Statistical tests work by calculating a test statistic - a number that describes how much the relationship between variables in your test differs from the null hypothesis of no relationship.. It then calculates a p value (probability value). The p-value estimates how likely it is that you would see the difference described by the test statistic if the null ...
Null Hypothesis Statistical Testing (NHST)
Null hypothesis testing relates only to the statistical hypothesis. I want to check my claim that CHOP's female workforce really is different than women generally as far as height. I take a sample of 20 women employed at CHOP and discover that while the average height for women in the USA is 163.2 cm, the average height of our 20 female ...
Null hypothesis
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...
An Introduction to Statistics: Understanding Hypothesis Testing and
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
Null hypothesis significance testing: a short tutorial
Abstract: "null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely". No, NHST is the method to test the hypothesis of no effect. I agree - yet people use it to investigate (not test) if an effect is likely.
8.3: Sampling distribution and hypothesis testing
Introduction. Understanding the relationship between sampling distributions, probability distributions, and hypothesis testing is the crucial concept in the NHST — Null Hypothesis Significance Testing — approach to inferential statistics. is crucial, and many introductory text books are excellent here. I will add some here to their discussion, perhaps with a different approach, but the ...
A Beginner's Guide to Hypothesis Testing: Key Concepts and Applications
Let's understand the hypothesis testing basics and explore its applications together. What is hypothesis testing in statistics? Hypothesis evaluation is a statistical method used to determine whether there is enough evidence in a sample of data to support a particular assumption. A statistical hypothesis test generally involves calculating a ...
ST 511
A null distribution is a sampling distribution under the assumption of the null hypothesis. It describes how that statistic would vary from sample to sample, if the null hypothesis were true. We can use theory or simulation techniques to model this distribution if our assumptions hold! Theory Based Methods. Assumptions for single proportion
Null Hypothesis
Null hypothesis, often denoted as H0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. Learn more about Null Hypothesis, its formula, symbol and example in this article
12.1: Two Variances F Test
The hypothesis testing procedures for testing claims about two population parameters is performed in the same way as the hypothesis testing procedures for one population parameter. ... Consider the following examples of statistical claims that involve the parameters about two populations. ... Both tests suggest that we DO NOT reject the null ...
Hypothesis Testing on Population Proportion (pdf)
Statistics document from Concordia University, 7 pages, Hypothesis Testing on Population Proportion Yufeng Shi March 31, 2023 Theoretical Foundation of Hypothesis Testing Sometimes we would like to test a hypothesis about the true population proportion p rather than true population mean µ. For example, when th
Estimation and testing of expectile regression with efficient
Subsampling strategy plays a crucial role in statistical inference for massive data owing to its computing and storage superiority. The parameter estimation and hypothesis testing of expectile regression for massive data is of concern. This paper offers an alternative to the traditional asymmetric least square (ALS) estimator via smooth approximation of loss function. Then, an efficient ...

Have a thesis expert improve your writing

Null and Alternative Hypotheses | Definitions & Examples

Table of contents

Examples of null hypotheses

Examples of alternative hypotheses

Test-specific

Cite this Scribbr article

Is this article helpful?

Shaun Turney

9.1 Null and Alternative Hypotheses

Example 9.1

Example 9.2

Example 9.3

Example 9.4

Collaborative Exercise

Null Hypothesis Definition and Examples

How to State a Null Hypothesis

Null Hypothesis Examples

Why Test a Null Hypothesis?

Hypothesis Testing: Uses, Steps & Example

What is Hypothesis Testing?

Using Hypothesis Tests

5 Steps of Significance Testing

Hypothesis Testing Example

Limitations

Share this:

Reader Interactions

Comments and Questions Cancel reply

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

How to Write a Null Hypothesis

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

Examples of Null Hypotheses

When Do We Reject The Null Hypothesis?

Why Do We Never Accept The Null Hypothesis?

Why Do We Use The Null Hypothesis?

Purpose of a Null Hypothesis

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

What is the difference between a null hypothesis and an alternative hypothesis?

What are some problems with the null hypothesis?

Why can a null hypothesis not be accepted?

Is a null hypothesis directional or non-directional?

Null Hypothesis Definition and Examples, How to State

Why is it Called the “Null”?

Why Do I need to Test it? Why not just prove an alternate one?

How to State the Null Hypothesis from a Word Problem

How to State the Null Hypothesis: Part Two

13.1 Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Key Takeaways

Share This Book

Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Long Descriptions

Media Attributions

Share This Book

Have a language expert improve your writing

Choosing the Right Statistical Test | Types & Examples

Table of contents

Prevent plagiarism. Run a free check.

Statistical assumptions

Types of variables

Regression tests

Comparison tests

Correlation tests

Here's why students love Scribbr's proofreading services

Cite this Scribbr article

Is this article helpful?

Rebecca Bevans

A Beginner's Guide to Hypothesis Testing: Key Concepts and Applications

What is hypothesis testing in statistics?

The P-value in Hypothesis Testing

Statistical Hypothesis Testing for Beginners: A Step-by-Step Guide

STEP 1: Define the Hypothesis