slip stick experiment

ME 270: Basic Mechanics I

A stick/slip friction experiment.

Say we consider a simple experiment of balancing a wooden rod on two fingers. The finger on the left, (1), will remain stationary, whereas the finger on the right, (2), will be moved toward the left. For the sake of discussion, let's assume that the coefficient of static friction between each finger and the rod is the same, μ S .

As finger (2) is moved to the left, the rod will need to slip with respect to one of the two fingers. At which finger with the rod slip?

We know that slipping will occur when a friction force reaches its maximum value, the value of the μ S times the normal force. So, the answer is: the finger with the smallest normal force on the rod is where slipping will occur. The analysis below shows that the finger furthest away from the center of mass, G, will slip on the rod . The finger at which slipping occurs has a friction force of μ K N where μ K   is the coefficient of kinetic friction. Note that typically   μ S  >  μ K .

Once the distance between each finger and G approaches the same value, then what happens? Here it gets a little more complicated. The friction force at each finger must be the same. The normal force at the sticking finger will continue to decrease until the maximum friction force is reached, causing it to now slip, and therefore will stick at the other finger.

Animation Consider the animation from a simulation of this problem shown below. Here the moving finger on the right starts out closer to the center of mass. As this finger moves to the left, the distance between the left finger and the center of mass decreases, eventually to the point where the normal force at the left finger has increased enough for sticking. At this point the finger on the right slips.

This cycle of sticking and slipping at the two fingers continues until the two fingers come together with the center of mass half way between the two fingers . This will ALWAYS occur, regardless of the initial positioning of the two fingers! Try it on your own.

Purdue University

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 14 December 2023

How frictional slip evolves

• Songlin Shi   ORCID: orcid.org/0000-0002-7321-9279 1 ,
• Meng Wang   ORCID: orcid.org/0000-0002-8304-3430 1 ,
• Yonatan Poles   ORCID: orcid.org/0009-0005-6061-9045 1 &
• Jay Fineberg   ORCID: orcid.org/0000-0002-8381-6675 1  

Nature Communications volume  14 , Article number:  8291 ( 2023 ) Cite this article

3562 Accesses

1 Citations

3 Altmetric

Metrics details

• Mechanical engineering
• Surfaces, interfaces and thin films

Earthquake-like ruptures break the contacts that form the frictional interface separating contacting bodies and mediate the onset of frictional motion (stick-slip). The slip (motion) of the interface immediately resulting from the rupture that initiates each stick-slip event is generally much smaller than the total slip logged over the duration of the event. Slip after the onset of friction is generally attributed to continuous motion globally attributed to ‘dynamic friction’. Here we show, by means of direct measurements of real contact area and slip at the frictional interface, that sequences of myriad hitherto invisible, secondary ruptures are triggered immediately in the wake of each initial rupture. Each secondary rupture generates incremental slip that, when not resolved, may appear as steady sliding of the interface. Each slip increment is linked, via fracture mechanics, to corresponding variations of contact area and local strain. Only by accounting for the contributions of these secondary ruptures can the accumulated interface slip be described. These results have important ramifications both to our fundamental understanding of frictional motion as well as to the essential role of aftershocks within natural faults in generating earthquake-mediated slip.

Similar content being viewed by others

Slip-rate-dependent friction as a universal mechanism for slow slip events

Nucleation fronts ignite the interface rupture that initiates frictional motion

Integrated rupture mechanics for slow slip events and earthquakes

Introduction.

Slip is the major vehicle for frictional dissipation 1 , 2 , 3 , 4 , 5 , 6 . What, then, determines the ‘slip budget’, which we define as the slip distribution in space-time? The slip budget is intimately related to the energy dissipation mechanisms associated with frictional sliding 7 , 8 , natural earthquakes 2 , 9 , 10 , 11 , 12 , 13 and related phenomena such as seismic estimates of fracture energy 14 , 15 , 16 . Understanding the details of the slip budget is, therefore, a key ingredient to unraveling the complex physical processes that are embodied in the ‘everyday’ phenomenon that we call ‘friction’.

How does frictional slip take place? Experiments have shown that slip initiates via the nucleation of rapid interface ruptures 3 , 4 , 5 , 17 , 18 , 19 , closely akin to earthquakes 14 , 15 , 20 , 21 . These ruptures are shear cracks 4 , 18 , 19 that propagate along the frictional interface that separates contacting elastic bodies and break the spatially extended ensemble of contacts that defines the interface. Slip immediately ensues at each point traversed by a rupture 5 . One might expect that, once the initial rupture ‘breaks’ the interface, slip of the entire interface could occur via continuous sliding that would proceed unimpeded until the applied shear stress within the sample is released. Surprisingly, direct measurements have shown that the initial rapid slip in the immediate wake of rapid rupture fronts is both finite and quite small (<20 µm), while the total slip of each macroscopic stick-slip event is 1–2 orders of magnitude greater 5 , 12 , 14 , 15 , 22 , 23 , 24 , 25 , 26 . What physical mechanism governs the total slip?

In our experiments we perform a detailed characterization of all of the interface rupture dynamics from the onset to completion of interface slip within each stick-slip event. We will show that numerous, nearly ‘invisible’ secondary interface ruptures propagate within a single stick-slip event. Concurrent slip measurements on the frictional interface will yield a nearly complete picture of the slip budget. While the stress and contact variations caused by each of these ‘secondary’ ruptures is extremely small, their combined slip is significant; nearly all of the slip within the interface is directly generated by these myriad, and nearly undetectable, secondary rupture events.

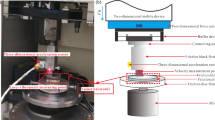
Our experimental system 4 , 27 (Fig.  1a, b ) consists of two polyvinyl chloride (PVC) blocks that are pressed together to construct a frictional interface of length x  = 200 mm and width z = 5.6 mm. The longitudinal, \({C}_{{{{{{\rm{L}}}}}}}\) , shear, \({C}_{{{{{{\rm{S}}}}}}}\) , and Rayleigh \({C}_{{{{{{\rm{R}}}}}}}\) waves speeds in PVC are, respectively 1886, 1067 and 983 ms –1 . The blocks were first compressed by applying a normal force F N  = 4300 N (3.84 MPa nominal stress) in the \(y\) direction. The shear force, \({F}_{{{{{{\rm{S}}}}}}}\) , was then increased slowly until a stick-slip sequence initiated. Upon initiation, we continuously and concurrently monitored: each strain component at 5 locations at a 1.16 MHz rate, the real contact area \(A(x,\, z,\, t)\) along the entire interface at 580,000 frames/sec with an x × z resolution of 1280 × 8 pixels, and the displacements \({{u}_{x}}^{+}(x,\, t)\) and \({{u}_{x}}^{-}(x,\, t)\) of the upper and lower blocks at 30 spatial points within the central 3.6 mm of the interface. These displacements were measured by correlating the profiles of grooves engraved on both sides of the interface (Methods and Fig.  1d ). These micro-scale grooves have negligible influence on the rupture propagation, resulting strain fields and the value of the fracture energy, as demonstrated in Supplementary Figs.  1 , 2 and Methods. Slip \({u}_{x}\left(x,\, t\right)={{u}_{x}}^{+}\left(x,\, t\right)-{{u}_{x}}^{-}(x,\, t)\) , was obtained at each point at a rate of 560,000/sec with a 0.5 μm resolution (Methods).

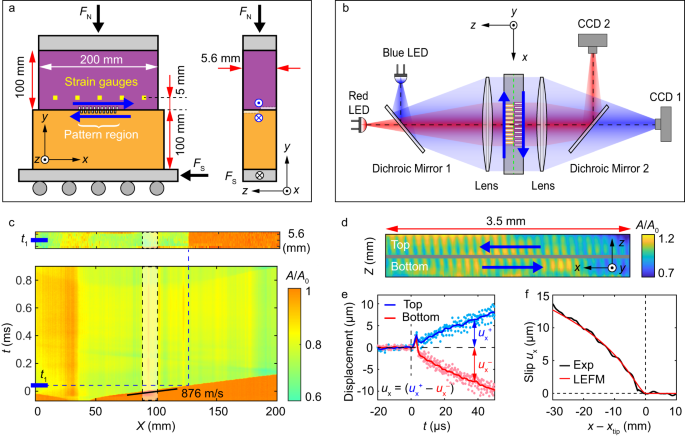
a PVC blocks of thickness W  = 5.6 mm are compressed under a normal force, \({F}_{{{{{{\rm{N}}}}}}}\) . Shear force, \({F}_{{{{{{\rm{S}}}}}}}\) , is applied to the lower block. Five miniature rosette strain gauges (green squares), 5 mm above the interface, are equidistantly distributed in x . Grooves are engraved (spatial period 120 μm) between \(90 \, < \, x \, < \, 110\)  mm at \(0 \, < \, z \, < \, W/2\) (top block) and \(W/2 \, < \, z \, < \, W\) (bottom block). b Optical system for real contact area, \(A\left(x,\, z,\, t\right),\,\) and slip measurements. The interface is illuminated by blue and red LED light sheets, which are separated by dichroic mirrors. Each light sheet undergoes total internal reflection at the PVC/air interface. Transmitted blue (red) light, captured by fast camera, CCD1 (CCD2) measures \(A\left(x,\, z,\, t\right)\) over the entire (grooved section of the) interface. CCD1 provides rupture dynamics via the space-time variations of \(A\left(x,\, z,\, t\right)\) . CCD2 monitors simultaneous displacements of both sets of grooves. c Typical \(A\left(x,\, z,\, t\right)\) measurement at the onset of a stick-slip event. Upper panel: a 2D snapshot of \(A\left(x,\, z,\, {t}_{1}\right)/A\left(x,\, z,\, {t}_{0}\right)\) , where \({t}_{0}\)  = 0 is a reference time immediately prior to the event and \({t}_{1}\sim 40\)  μs after the onset of the initial interface rupture. Lower panel: \({A\left(x,\, t\right)/A\left(x,\, {t}_{0}\right)=\left\langle A\left(x,\, z,\, t\right)/A\left(x,\, z,\, {t}_{0}\right)\right\rangle }_{z}\) of this event. Rupture fronts are points where \(A\left(x,\, t\right)/A\left(x,\, {t}_{0}\right)\) falls from 1. d CCD2: Images of grooved regions. The gray line separates grooves engraved on the top and bottom blocks. Blue arrows indicate their relative motion. e Measured displacements (see Methods) at the interface of the top (blue, \({{u}_{x}}^{+}\) ) and bottom (red, \({{u}_{x}}^{-}\) ) blocks when the rupture in ( c ) traversed the grooved section. Lines: \({{u}_{x}}^{+}\) and \({{u}_{x}}^{-}\) smoothed over 1 µs. f Black line: slip, \({u}_{x}={{u}_{x}}^{+}-{{u}_{x}}^{-}\) , at the interface as a function of the distance from the crack tip, \({x}_{{{{{{\rm{tip}}}}}}}\) . Red line: the slip profile predicted by the LEFM, with fitted fracture energy Γ 1  = 1.3 J m –2 .

In Fig.  1c–f , we present typical measurements of \(A\left(x,\, z,\, t\right)/A\left(x,\, {z,\, t}_{0}\right)\) , \({{u}_{x}}^{-}(x,\, t)\) , \({{u}_{x}}^{+}(x,\, t)\) , and \({u}_{x}\left(x,\, t\right)\) for a right-propagating sub-Rayleigh rupture (velocity, \({C}_{{{{{{\rm{f}}}}}}}=0.89{C}_{{{{{{\rm{R}}}}}}}\) at x  = 100 mm) that initiated at x  = 40 mm and traversed the region 90 < x  < 100 mm where slip was measured. \(A\left(x,\, {z,\, t}_{0}\right)\) denotes the initial contact area at a time \({t}_{0}\) prior to rupture initiation. Each rupture front reduces \(A\left(x,\, z,\, t\right)\) by partially detaching the interconnecting contacts that form the interface. \(A\left(x,\, z,\, t\right)/A\left(x,\, {z,\, t}_{0}\right)\) provides the location, \({x}_{{tip}}\) and front velocity \({C}_{{{{{{\rm{f}}}}}}}\) of each rupture front as it traverses the interface. At each spatial point traversed by a rupture, slip takes place.

Both \({{u}_{x}}^{+}(x,\, t)\) , and \({{u}_{x}}^{-}(x,\, t)\) for the first rupture in Fig.  1c are presented in Fig.  1e . As the rupture tip traverses each point, surprisingly both \({{u}_{x}}^{+}\) and \({{u}_{x}}^{-}\) are first displaced (for about 5 µs) in the same direction. While this effect precedes rapid motion 5 , it does not contribute to slip, \({u}_{x}={{u}_{x}}^{+}-{{u}_{x}}^{-}\) , as \({{u}_{x}}^{+}\) and \({{u}_{x}}^{-}\) cancel each other. Beyond this interval, slip \(({u}_{x} \, > \,0)\) initiates via roughly antisymmetric displacement of the two blocks (Fig.  1e ), although perfect anti-symmetry of \({{u}_{x}}^{\pm }\) is not always observed. Figure  1f reveals that the \({u}_{x}(x-{x}_{{{{{{\rm{tip}}}}}}})\) structure generated by the sub-Rayleigh rupture compares well with the slip profile calculated with Linear Elastic Fracture Mechanic (LEFM) with a cohesive model 28 (Methods, Supplementary Fig.  1a, b ).

The first interface rupture produces the relatively large contact area drop, \(\Delta A/{A}_{0}\, \approx \,0.26\) shown in Fig.  1c . Following this initial drop, subsequent weaker and considerably less distinct contact area reductions occur (e.g., beyond \({t}_{1}\) in Fig.  1c ). Ostensibly, the apparent ‘constant’ value of A / A 0 for \(t \, > \,{t}_{1}\) could suggest a continuously sliding process; i.e., ‘dynamic friction’. A closer look (Fig.  2a ), via (Methods) the normalized differential contact area \(\overline{{\partial }_{t}A\left(x,\, t\right)}\) at each spatial location, x , reveals a different picture. Within the first 3 ms of slip in Fig.  1c , numerous sequential secondary ruptures 6 , 16 , 29 , 30 , 31 , 32 take place after the main rupture. These secondary ruptures, revealed by \(\overline{{\partial }_{t}A\left(x,\, t\right)},\,\) are nearly invisible in the contact area measurements, as resulting \(\Delta A/{A}_{0}\) are extremely small (Supplementary Table  1 ).

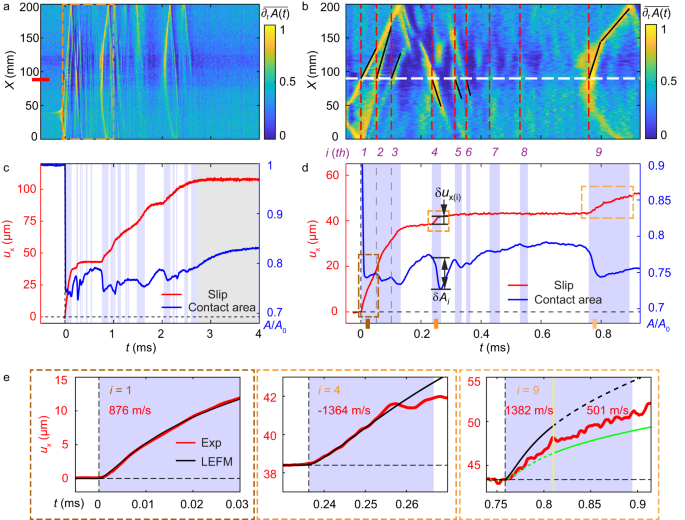
a Normalized differentiation \(\overline{{\partial }_{t}A\left(x,t\right)}\) reveals numerous sequenced ruptures occurring in the 3 ms following the initial rupture. b The first 1 ms of ( a ). Vertical dashed lines labeled by integers denote sequential ruptures as they pass the slip measurement location. c , d The detailed evolution of the contact area (blue line) and the slip (red line) in ( a , b ), respectively. The light purple backgrounds denote the temporal windows over which the labeled ruptures continued to propagate within the interface. \(\delta {u}_{i}\) and \(\delta {A}_{i}\) denote the slip and contact area drop precipitated by i th rupture. The slip measured at the X position denoted in ( a ) (red mark) and ( b ) (white dashed line). The slopes of the black lines in ( b ) denote the local rupture velocities as ruptures cross the measurement section. e Three typical ( i  = 1, 4, 9) slip profiles (red) are compared to LEFM predictions (black). i  = 1 is sub-Rayleigh, while i  = 4 is supershear. The i  = 9 rupture is supershear until the yellow line, it then transitions to sub-Rayleigh. Black and green curves are LEFM predictions within the supershear and sub-Rayleigh ranges, respectively.

Details of secondary ruptures are presented in Fig.  2a, b . Red dashed lines denote the times when each secondary rupture arrived at the region ( x  ~ 90 mm) where slip was measured. The corresponding slip and \(\Delta A\) variations within each time interval, are presented in Fig.  2c, d . Each sequential rupture causes a drop in contact area accompanied by slip. This sequence of secondary ruptures only ceases after t  ~ 3 ms, when the contacting blocks become locked and \(A(x,\, z,\, t)\) commences to reheal (or ‘age’) as \(A(t)\) increases logarithmically in time 5 , 33 , 34 , 35 .

The slip at each spatial point is not smooth, but, instead, increases in discrete increments; each secondary rupture initiates augmented slip at each spatial location, immediately upon the rupture’s passing. The slip initiated by each rupture continues until information (via shear waves) that the rupture has either arrested or traversed the entire interface reaches the measurement point. Some ruptures, e.g., between 0.5 and 0.8 ms, while detectable, are so weak that they are not explicitly marked. These extremely weak ruptures still have a marked effect; they prevent aging of \(A\left(x,\, t\right)\) and give rise to apparent ‘noise’ together with a very slight increase of slip in the \({u}_{x}(t)\) measurements. The total slip reaches 120 µm, an order of magnitude greater than the ‘large’ slip generated by the initial rupture (Fig.  2c, d ).

For convenience, in Fig.  2 we label the more prominent secondary ruptures by their chronological order. The durations of the first three ruptures overlap, as they propagate simultaneously within the interface. The 2nd and 3rd ruptures are formed by reflections from the x  = 0 mm boundary. The 2nd rupture is a supershear rupture ( v  >  C S ) 36 , 37 , 38 , while the 3rd rupture propagates close to the Rayleigh wave speed, C R . We find that the majority of the observed sequential ruptures are supershear, in contrast to other observations 16 , 29 . This difference may be attributed to significant differences in stored elastic energy, prior to nucleation of the initial ruptures. In our experiment, initial ruptures attain speeds, v  > 0.8 C R , whereas v  ~ 0.1 C R in previous observations of secondary ruptures 16 , 29 . Rapid initial ruptures (analogous to an earthquake’s ‘main shock’) tend to trigger numerous secondary supershear ruptures; such supershear aftershocks have not yet been frequently identified in natural earthquakes 39 .

Generally, the mode of each secondary rupture (sub-Rayleigh vs . supershear) tends to be retained during propagation. In some cases, however, a rupture can transition from sub-Rayleigh to supershear 36 , 37 , 40 , 41 , or vice versa 41 . An example is presented in the i  = 9 rupture (Fig.  2e , right panel) that nucleates as supershear before transitioning to sub-Rayleigh. Such transitions may occur when ruptures encounter barriers or obstacles 3 , 41 .

Often, in our system, additional, ‘bunched’ rupture sequences occur, such as those occurring during t  = 0.8–1.2 and 2–2.4 ms in Fig.  2 . Each of these proceeds as in Fig.  2a . The intervals between these slip sequence clusters are consistent with the ~1 ms time scale, defined by our system’s resonant response time (Methods, Supplementary Figs.  3 , 4 ). The weak forcing caused by any small resonant ‘backlash’ is sufficient to trigger additional rupture sequences.

The fracture energy of a frictional interface is a dynamic quantity. The fracture energy of the i th rupture, Γ i is determined by both the contact area which increases with the normal stress, \({\sigma }_{{yy}}\) , and the contacting time Δ t 42 , 43 , 44 . The ‘invisible’ character of secondary ruptures, stems from the fact that the intervals, \(\Delta {t}_{i}\) , since the previous rupture are generally quite small (often less than 10–20 μs, as in the 5th and 6th ruptures in Fig.  2b, d ) and leave little time for \(A(t)\) to reheal. This contrasts with the significant contact aging 5 , 33 , 34 , 35 over the interval \(\Delta {t}_{1}\) before the initial rupture. Since \({\sigma }_{{yy}}\) is constant, we can assume that the fracture energy of the i th rupture, \({\varGamma }_{i}\) , is proportional to the contact area drop δA i that they precipitate (see Fig.  2d ); therefore Γ i  =  Γ 1 · ( δA i / δA 1 ) (Methods). As Fig.  2d demonstrates, δ A i are generally quite small, often below 5% of \(\delta {A}_{1}\) (Supplementary Table  1 ). These minute δ A i explain the extreme velocities of the secondary ruptures, as when \({\varGamma }_{i}\to 0\) , any small (but finite) driving stress will cause a rupture to immediately accelerate to extreme values.

We now examine three specific ruptures (1st, 4th, and 9th) that produce finite slip steps. In Fig.  2e , we show that LEFM 28 , 45 successfully describes the slip profiles resulting from both sub-Rayleigh (1st) and supershear (4th) ruptures (Methods, Supplementary Fig.  5 ). Secondary ruptures are not, necessarily, well-defined rupture modes, as in the 9th rupture that transitioned from supershear to sub-Rayleigh modes. Even here, LEFM predictions are close to measured values. Such transitions can (and should) affect the slip profile at a given point at the interface. As no theoretical framework exists that predicts the slip profile in the wake of a rupture that transitions to a different rupture mode (as in the 9th rupture), we assume that superposition of the slip profiles of the different rupture modes can be used.

In Fig.  3a , we present strain gauge measurements that accompany the secondary ruptures described in Fig.  2 . The largest \({\varepsilon }_{{ij}}\) component, \({\varepsilon }_{{xx}}\) , is presented. \({\varepsilon }_{{ij}}(x-{x}_{{{{{{\rm{tip}}}}}}})\) of the first ruptures in each stick-slip sequence are reproduced well by LEFM (Supplementary Fig.  1c ). Secondary ruptures often propagate within the tail of previous ruptures, so secondary ruptures may dynamically vary the residual stresses in both space and time along interfaces. This leads to dynamically induced stress inhomogeneities within interfaces. Both this effectively variable residual stress and the very small stress changes induced by secondary ruptures introduce challenges in accurately comparing the spatiotemporal strain profile to theory. Despite these difficulties, we can utilize the peak-to-peak strain variations, \({{\delta }{\varepsilon }}_{{ij}}^{{{{{{\rm{osc}}}}}}}\) , that are excited in close proximity to passing rupture tips, to perform a rough comparison to LEFM predictions 4 . Examples of \({{\delta }{\varepsilon }}_{{xx}}^{{{{{{\rm{osc}}}}}}}\) are denoted in Fig.  3a . It is clear that the signal levels of \({{\delta }{\varepsilon }}_{{ij}}^{{{{{{\rm{osc}}}}}}}\) , while appearing ‘noisy’, are actually far about our measurement noise (magenta dashed lines in Fig.  3b, c ). These fluctuations are entirely due to the passage of secondary ruptures.

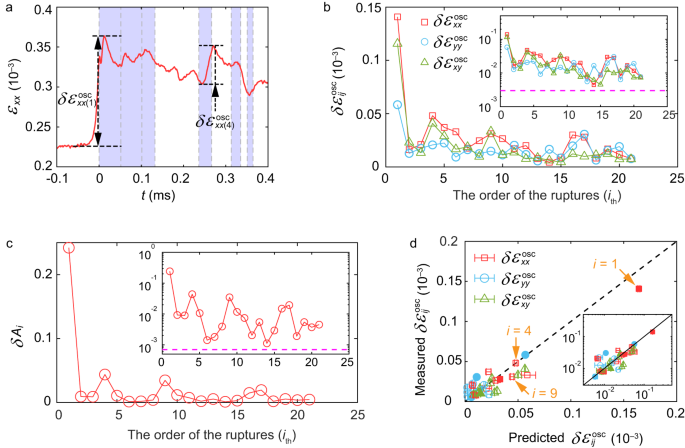
a Strain gage signals \({{\varepsilon }}_{{xx}}\) . Noted are strain oscillation amplitudes, \({\delta }{{\varepsilon }}_{{xx}}^{{{{{{\rm{osc}}}}}}}\) , from the 1st and 4th ruptures of the sequence in Fig.  2 . Shading denotes, as in Fig.  2 , rupture durations. b The strain oscillation amplitudes of three components ( \({\delta }{{\varepsilon }}_{{xx}}^{{{{{{\rm{osc}}}}}}}\) , \({\delta }{{\varepsilon }}_{{yy}}^{{{{{{\rm{osc}}}}}}}\) , \({\delta }{{\varepsilon }}_{{xy}}^{{{{{{\rm{osc}}}}}}}\) ) due to a rupture sequence, as a function of their order of appearance. c The contact area drops \({{\delta }A}_{i}\) of the sequence presented in ( a , b ). Insets in ( b, c ) are plotted in logarithmic y-coordinates; magenta horizontal lines are measurement noise levels. d Comparison of measured \({\delta }{{\varepsilon }}_{{ij}}^{{{{{{\rm{osc}}}}}}}\) with LEFM predictions, using the fracture energy \({{\Gamma }}_{i}={{\Gamma }}_{1}{\cdot }[{{\delta }A}_{i}/{{\delta }A}_{1}]\) as input. \({{\Gamma }}_{1}=1.3\,{{{{{\rm{J}}}}}}{{{{{{\rm{m}}}}}}}^{-2}\) . Filled and open symbols represent sub-Rayleigh and supershear ruptures, respectively. The \({\delta }{{\varepsilon }}_{{xx}}^{{{{{{\rm{osc}}}}}}}\) of the ruptures i  = 1, 4, 9 in Fig.  2e are marked by arrows. Inset: logarithmic coordinates.

Figure  3b compares the peak-peak strain oscillations, \({{\delta }{\varepsilon }}_{{ij}}^{{{{{{\rm{osc}}}}}}}\) , of all strain components as a function of the order of the appearance of the secondary ruptures, as denoted in Fig.  2c . Figure  3c presents the corresponding drop \(\delta {A}_{i}\) in \(A/{A}_{0}\) for \(i \, < \,22\) . As the mean \({\sigma }_{{yy}}\) is constant, the \(\delta {A}_{i}\) represent the relative fracture energy \(\delta {\varGamma }_{i}\) of each rupture. ( \(\delta {\varGamma }_{i}\) are set by both the healing interval, \(\Delta {t}_{i},\,\) between sequential ruptures and their velocity 43 ). In the \(\Delta {t}_{i}\; \approx \) 20–100 μs between secondary ruptures, the recovery of \(A\left(x,\, t\right)\) is nearly imperceptible, \(\delta A\left(x,\, t\right) \, < \,1\%\) 5 . This is barely within our 0.2–0.5% measurement resolution. In Fig.  3d we compare all of the measured \({{\delta }{\varepsilon }}_{{ij}}^{{{{{{\rm{osc}}}}}}}\) with their values predicted by LEFM (for both sub-Rayleigh or supershear solutions) supplemented by a simple cohesive zone model 28 (see Methods) whose sole input is Γ i . The measured and predicted strain oscillations agree quite well; LEFM quantitatively describes the behavior of secondary ruptures. To perform this comparison, we only considered isolated ruptures whose velocities could be quantitatively determined (Supplementary Table  1 ). Weak ruptures with \({C}_{{{{{{\rm{f}}}}}}}\to {C}_{{{{{{\rm{R}}}}}}}\) were excluded, as in this range any small uncertainty in \({C}_{{{{{{\rm{f}}}}}}}\) could result in significant uncertainties in predicted strains.

We define an ‘event’ as containing both the initial rupture (indexed by ‘1’) together with all of its subsequent accompanying secondary ruptures. We define the total slip of an event, u tot as the integrated slip of all of these ruptures. Whereas the slip of the initial rupture is typically \({u}_{1}\sim 10-20\,{{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}\) we find that \({u}_{{{{{{\rm{tot}}}}}}}\sim 100-200\,{{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}\) (e.g., Figs.  1 , 2 ). How much of u tot is directly due to the secondary ruptures? In Fig.  4a we present the evolution of u x from the time of the initial rupture until the cessation of slip, in two representative events. As we would expect, u tot is linearly related to the overall shear stress drop, Δ σ xy (Fig.  4a – inset). This observation is consistent with the linear relation of the stress drop and slip in earthquakes 13 . On the other hand, within each event, slip distributions of both the primary and secondary ruptures can (and will) vary considerably, as in the examples presented. In Fig.  4b , the number of ruptures whose slip exceeds \(\delta u\) , is presented for both the events presented in Fig.  4a (green and red symbols) as well as (blue symbols) the cumulative results of 7 ruptures (each from a different experiment). These distributions (inset - Fig.  4b ) collapse onto one another, when both normalized and scaled by their approximate seismic moment M 0  =  G · S · δu i . G and S are, respectively, the shear modulus and total interface area while δu i is the slip of each secondary rupture 13 (Methods).

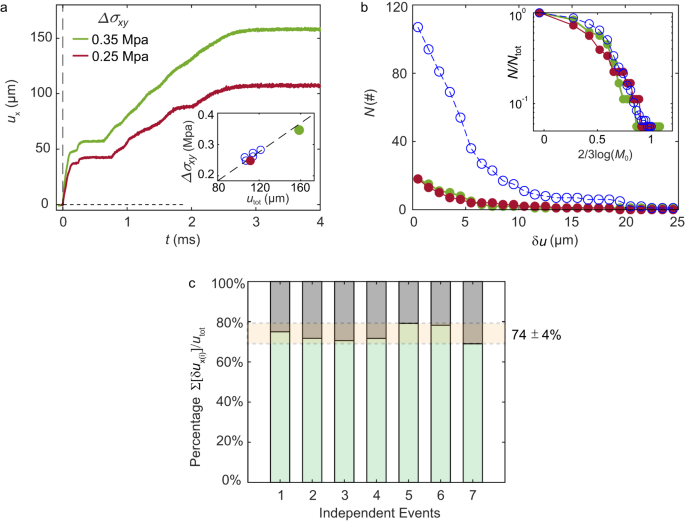
a The slip profiles of two typical events (with different sequenced ruptures) under different global stress drops, Δ σ xy , of 0.25 and 0.35 Mpa. The global stress drop is defined as the difference between the initial stress before the first rupture occurs and the averaged stress after the first rupture until slip cessation. Higher global stress drops Δ σ xy correspond to larger total slips u tot . Inset: global stress drop and total slip from seven events, u tot ∝ Δ σ xy , the reference dashed line passes through (0,0). b Statistics of the number of sequenced ruptures whose slip exceeds \({{{{{\rm{\delta }}}}}}{u}_{x}\) . Blue open symbols are the statistics from 7 different events. Red and green symbols are the corresponding events from Fig.  4a . Inset: statistics of corresponding (normalized) magnitudes. c Percentage of total slip that is directly due to ruptures (see text) in 7 different events (from different experiments); ruptures traversing the measurement region directly account for at least 74% ± 4% of the total slip for each event.

The M 0 of the secondary ruptures fall within 1–50 N·m. While most of these ruptures traversed the entire length of our experimental ‘fault’, their slip, \(\delta {u}_{i},\,\) varies greatly. Slip variation is the main reason for the broad distribution of \({M}_{0}\) in Fig.  4b ; ruptures precipitating large slip are far less frequent than those with smaller slip. The scaling in Fig.  4b is similar to the Gutenberg-Richter (G-R) law 9 that describes the moment distribution for natural earthquakes; power law behavior is observed on the right side of the curve with a roll-off (top-left corner) for small equivalent magnitudes 13 . The roll-off in Fig.  4b could be due (as surmised for earthquakes 13 ) to our lack of resolution in detecting ruptures that generate extremely small slips. Our results may suggest that the main reason for the spread of \({M}_{0}\) is not variations of the spatial extent of the different events, since the ruptures observed here all roughly span the interface length. Instead, \({M}_{0}\) is governed by \(\delta {u}_{i}\) . \(\delta {u}_{i}\) are mainly controlled by the fracture energy, \({\varGamma }_{{{{{{\rm{i}}}}}}}\) , of each rupture, which, itself is governed by the healing time \(\Delta {t}_{i}\) . This could also be true for aftershock moments within natural faults 44 .

Let us now consider the ‘slip budget’ contributed by dynamic ruptures. To what extent is the total measured slip due to the nearly ‘invisible’ secondary ruptures? In Fig.  4c we compute the percent of \({u}_{{tot}}\) contributed solely by dynamic secondary ruptures in 7 typical experiments, including only ruptures whose stress drops exceeded twice the measurement noise. Surprisingly, we find that main and these secondary ruptures account for approximately 74% of \({u}_{{tot}}.\) Since we are certainly missing the smallest ruptures, Fig.  4c , provides a lower bound for the slip budget.

We have presented a comprehensive study of the origins of frictional slip. The specific events described in Figs.  1 – 4 are wholly representative of the numerous stick-slip events that we have analyzed. In this rather standard block-on-block frictional motion, slip is entirely dominated by myriad, seemingly ‘invisible’ secondary frictional ruptures. In all cases that were amenable to detailed analysis (i.e., sufficiently large signals as well as secondary ruptures that were isolated, in time, from other ruptures), we have shown that these ruptures can be effectively described using LEFM supplemented by a simple cohesive zone model. The apparent ‘invisibility’ of the secondary ruptures, is due to the, often minute, healing intervals available to sequential ruptures; as aging is approximately logarithmic in time 33 , 34 , 35 , 44 . This minute recovery of \(\delta {A}_{i}\sim {\varGamma }_{i}\) gives rise to correspondingly small variations in both the stress changes, \(\delta {\varepsilon }_{{ij}}\) , and slip, \(\delta {u}_{i}\) . While all of these quantities are quite small, since \({\varGamma }_{i}\to 0\) the velocities of secondary ruptures are generally extreme (the majority are supershear). At such small Γ secondary ruptures can be triggered by either (real) noise in the system or, simply, via reflected ruptures from the horizontal boundaries. The rupture-generated signals excite ‘apparent’ measurement noise that is significantly above our measurement accuracy. These effects would generally be hidden in global measurements and would appear as steady sliding. To detect them it is necessary to have sufficient temporal accuracy ( \({{{{{\rm{\mu }}}}}}{{{{{\rm{s}}}}}}\) time scales) together with the ability to observe and correlate all of these, seemingly, insignificant variations in \(A,\, \varepsilon\) , and \(\delta u\) . As we have shown in both Figs.  2e ,  3d , these miniscule and seemingly ‘disparate’ signals are indeed correlated via LEFM.

These findings provide a conceptually different view of the evolution of sliding that, macroscopically, is generally attributed to ‘dynamic friction’ at the transition from ‘static friction’, occurring after the initial rupture. Global measurements that average over spatial and significant temporal scales present a mean-field perspective of the average slip. These would manifest as the smooth curve assumed in empirical friction laws 7 , 23 . Such apparently continuous macroscopic motion that is, instead, driven by a sequence of small discrete events is also observed in the peeling dynamics of adhesive tape 46 . While the details are different than in the frictional system, the apparent slow and continuous macroscopic motion obtained when peeling an adhesive strip is actually produced by a discrete succession of nearly imperceptible rapid fronts, each producing a small and discrete amount of slip.

Now that the basic physics of secondary frictional ruptures are understood, we speculate that it may be possible to utilize this knowledge to control the amount of frictional slip that takes place in a given event. In principle, external excitation of numerous secondary ruptures should enhance overall frictional slip, while the insertion of barriers to rupture 3 could be a means to limit slip by arresting (trapping) secondary ruptures.

When we consider the energy dissipated by this process, the fracture energy released at the rupture tip, \(\sum {\varGamma }_{i}\sim \sum {({\tau }_{{{{{{\rm{p}}}}}}}-{\tau }_{{{{{{\rm{res}}}}}}})}_{i}\cdot {u}_{i}\) (Methods), is a relatively small part of the total dissipation. Here \({\tau }_{{{{{{\rm{p}}}}}}}\) and \({\tau }_{{{{{{\rm{res}}}}}}}\) are the ( \(i\) - dependent) peak and residual stresses. The majority of the frictional dissipation \(\sim {u}_{{{{{{\rm{tot}}}}}}}\cdot {\tau }_{{{{{{\rm{res}}}}}}}\) , is also related to the fracture process through \({u}_{{{{{{\rm{tot}}}}}}}\) , as most of \({u}_{{{{{{\rm{tot}}}}}}}\) is directly attributed (Fig.  4 ) to the rupture process. The dissipation and ‘damage’ (damage here is measured by the variation of the local contact area) imposed by the primary and secondary rupture processes are non-uniform along the interface. These ruptures, with their accompanying slip, introduce non-uniform residual strengths along the interface. This non-uniformity is retained upon the cessation of slip. While the interface strength at each point will heal via the approximate logarithmic aging in time 5 of A (Supplementary Fig.  6 ), any inhomogeneity of A , upon the cessation of slip, will be retained by this healing process. A ( x , t ) depends on the values of the residual strength at the cessation of slip, local stress levels and the time since slip cessation at each spatial point.

The complex framework of inhomogeneous and coexisting sequenced ruptures are statistically observed as aftershocks of large earthquakes within natural faults, e.g., G-R law (subfigure of Fig.  4b ). These myriad events are so numerous (and so small) that they are individually invisible and are generally only represented by statistical tools (e.g., Gutenberg-Richter analysis). The secondary ruptures that we observe are aftershocks, each is part of a swarm of rupture events in the immediate aftermath of any ‘main’ stick-slip event. These rupture sequences could provide a means to relate observed correlations between geodetically observed afterslip and seismically observed aftershocks 10 , 11 . These experiments provide valuable insights to complex fault processes, as detailed observation of individual ruptures within natural faults is currently extremely challenging.

We demonstrated that nearly invisible secondary ruptures that always follow the first rapid frictional ruptures predominantly shape the slip budget. The repeated breaking and localized healing along the interface, therefore, play a crucial role in governing the evolution of the ‘frictional tail’ that follows the onset of friction, as well as the relationship between after-slip and aftershocks.

Sample construction

We define x , y , z as, respectively, the sliding, normal loading, and surface thickness directions. The x  ×  y  ×  z dimensions of the top and bottom PVC blocks were 200.0 × 100.0 × 5.6 mm and 220.0 × 100.0 × 5.6 mm. Both blocks were polished to optical flatness with a roughness ~3 µm. The longitudinal wave speed C L and shear wave speed C S , were measured ultrasonically, yielding values C L  = 1886 ± 10 m s –1 (plane stress) and C S  = 1067 ± 10 m s –1 . These provide a Rayleigh-wave speed C R  = 983 ± 10 m s –1 and yield dynamic values of the Poisson ratio, ν  = 0.36, and Young’s modulus of E  = 4.18 GPa. The density of the PVC is 1350 kg m –3 .

Groove pattern engraving

The motion of grooved patterns on the frictional interface is used to track the slip of the interface. To avoid interference between the patterns on the upper and bottom blocks, groove patterns are only engraved on half of the width of each block; grooves extended over \(0 \, < \,z \, < \,W/2\) and \(W/2 \, < \,z \, < \,W\) , for the upper and lower blocks respectively (Fig.  1d ). This technique was used previously, when only a single block face was grooved 27 . Grooves were engraved in the center 20 mm (in \(x\) ) of the interface by means of a UV laser cutter, while half of the interface width was masked. Each groove was 60 µm wide and the periodicity between grooves was set to 120 µm. This procedure formed ridges and gaps of equal width, with a gap depth of 10–15 µm. The entire interface was then re-polished to remove any residual material, formed by the laser cutter, at the groove edges.

Loading system

The loading system was comprehensively described previously 4 . The top block was clamped at its upper edge, while the bottom block was attached to a low friction translational stage. A uniform normal load F N  = 4300 N, was applied at the initiation of each experiments and retained to be constant over the duration of each experiment. Once \({F}_{N}\) was set, an external shear force F S was quasi-statically applied to the bottom block in the negative x direction (from the left side of the bottom block, Fig.  1a ) with rate 10 µm s –1 . This slow loading rate ensures that F S is constant over the 3–4 ms duration that characterized the onset of each stick-slip event. After the normal load is applied, the time between the different events influences the value of the real area of contact (bare fracture energy), as the interface ages logarithmically with time; a longer aging time indicates a stronger binding interface. The waiting time for each event was controlled to determine the fracture energy of the first rupture in each stick-slip sequence. The fracture energies of secondary ruptures were determined by the interface evolution and healing times before each onset of a secondary slip.

Resonant timescale of the mechanical system

Like any mechanical system, our experimental system contains mechanical resonances that introduce an inertial timescale into our experiments. After the initial slip takes place, the loading frame itself will undergo slight oscillations, as these resonances are excited. These oscillations induce slight reloading of the system and may induce the excitation of new rupture sequences within the interface, which has been weakened after the passage of the first rupture sequence. As a result, we often observe successive slip sequences that are spaced in time at the system resonances. In Supplementary Fig.  3 we present the first 10 ms of motion in a typical experiment. The antisymmetric motion of the opposing blocks indicates slip ( u  =  u + – u – ) – which takes place over approximately the first 3 ms. For longer times, symmetric motion of u + and u – takes place that indicates the interface is locked with no slip is taking place. Over this time, the system is undergoing coherent resonant oscillations.

In Supplementary Fig.  4 , we present the variations of strains of all three components ε xx , ε yy , and ε xy , after striking the system with a steel rod ( \(\delta\) function excitation) while applying \({F}_{{{{{{\rm{S}}}}}}}\) at levels slightly below the onset of stick-slip (under same \({F}_{{{{{{\rm{N}}}}}}}\) ). The resulting Fourier spectra of the strain gauge signals in the center ( \(x=\) 100 mm) of the blocks produces resonant peaks at 1250 Hz and 400 Hz that correspond to oscillation periods of 0.8 ms and 2.5 ms. These oscillation time scales indeed match the temporal separation of rupture sequences in our experiments and also can be seen in the u + , u – measurements of Supplementary Fig.  1c , in for \(t \, > 3\,{{{{{\rm{ms}}}}}}\) when the interface is locked.

After the onset of rupture, these stress oscillations can drive additional rupture sequences (see Fig.  2a ) that initiate at these resonant time scales. We wish to emphasize that this effect, in no way, takes away from the generality of our results. It, instead, emphasizes that any type of small perturbation will indeed excite rupture sequences (with their resultant slip), once the interface is weakened by its initial rupture.

Contact area measurements and contact area differentiation

To image the interface under different scales of the field of view, we utilized two separate high-speed cameras (Fig.  1b ). The first high-speed camera (CCD1, Phantom v710), was used to visualize changes in the real contact area, \(A\left(x,\, z,\, t\right),\,\) over the entire interface at \(x\times z=1280\times 8\) pixel resolution. Each pixel was, therefore, mapped to an area \(\Delta x\times \Delta z=156\times 700\,{{{{{\rm{\mu }}}}}}{{{{{\rm{m}}}}}}.\) \(A\left(x,\, z,\, t\right)\) was measured via a light sheet that illuminated the entire interface at an angle well beyond the angle for total internal reflection between the PVC and air. As a result, transmitted light only passed through the contact points within each pixel, while light impinging non-contacting sections of the interface was reflected away from the interface. The transmitted light is therefore proportional to A ( x , z , t ) (top panel in Fig.  1c ). Signals were often averaged in the width z to provide A ( x , t ) (bottom panel in Fig.  1c ). The camera was operated at a frame rate of 580,000 frames/sec, enabling continuous measurements of A ( x , z , t ) at temporal intervals of Δ t  = 1.7 µs. To avoid interference and polarization effects, the interface was illuminated using an incoherent blue (460 nm) light source, a high-power LED (CBT-120). This camera has an approximate 9 bit resolution in intensity. After averaging in the \(z\) direction, a measurement noise level of the intensity of approximately 0.2% was achieved.

To resolve the weaker secondary ruptures, we utilized the differential contact area \({\partial }_{t}A\left(x,\, t\right)\) at each spatial location, \(x,\,\) along the interface. The normalized differential contact area \(\overline{{\partial }_{t}A\left(x,\, t\right)}\) (Fig.  2a ) is obtained through \(\overline{{\partial }_{t}A\left(x,\, t\right)}=[{\partial }_{t}A\left(x,\, t\right)-\partial {A}_{c}]/\Delta (\partial A)\) , where \(\partial {A}_{c}\) and \(\Delta \left(\partial A\right)\) are, respectively, the local threshold value of the background and the maximum values of the differentiated signal. To reduce noise in the differentiated signal, running averages in time (20 frames) and space (20 pixels) were used – effectively smoothing over an approximate 3 mm interval.

Interface displacements and slip measurements

The accurate determination of slip precisely at the interface poses a formidable challenge 27 , as rapid, high precision, simultaneous measurements of the relative motion of both contacting surfaces that form a frictional interface is required. The second high-speed camera (CCD2, Phantom v1611) utilized the same imaging technique, but instead was focused on the central \((\Delta x,\, \Delta z)=\) (10, 5.6) mm grooved section of the interface. Here the 560,000 frame/sec provided a continuous measurement of A ( x , z , t ) every 1.8 µs (Fig.  1d, e ). This region was illuminated by the same type of high-power LED (CBT-120) that produced a highly focused red (623 nm) light sheet. To measure the slip of the interface to high precision, an x  ×  z  = 3.65 × 5.6 mm region was imaged with a resolution of 512 × 32 pixels. This enabled visualization of 30 grooves with a spatial resolution in x and z directions of 7 µm and 175 µm for each pixel. Our slip measurements provide the mean slip of each x  ×  z  = 3.65 × 2.8 mm half-width section to 0.5 µm accuracy. The slip was detected as follows. A ( x , z , t ) was averaged in \(z\) to provide A ( x , t ). Sequential images in time of A ( x , t ) between each groove were then cross-correlated to provide \({u}^{\pm }\left(x,\, t\right)\) for each \(x\) . We are interested in obtaining the function \({u}^{\pm }(x-{x}_{{{{{{\rm{tip}}}}}}})\) . With CCD1 we both measured \({C}_{{{{{{\rm{f}}}}}}}\) and determined the tip location, \({x}_{{{{{{\rm{tip}}}}}}}(t)\) . Assuming \({C}_{{{{{{\rm{f}}}}}}}\) to be constant within the measurement time, we then converted the temporal measurements of \(\delta u(x,\, t)\) between each groove to estimate \({u}^{\pm }(x-{x}_{{{{{{\rm{tip}}}}}}})\) . A constant \({C}_{{{{{{\rm{f}}}}}}}\) provides translational invariance of the rupture front. All quantities are the functions of the argument \(x-{C}_{{{{{{\rm{f}}}}}}}t\) over the measurement interval. In particular, for grooves separated by a distance \(d\) , \({u}^{\pm }(x,\, t)\)  =  \({u}^{\pm }(x+d,\, t+d/{C}_{{{{{{\rm{f}}}}}}}).\) This enabled us to align each of the groove measurements to a reference point in the center of the measurement section and average over these independent measurements to obtain \({u}^{\pm }(x-{x}_{{tip}}).\) The relative slip, u  =  u + – u – was thereby obtained with a resolution of better than 0.5 μm as presented in Fig.  1e (blue u + and red u – curve). We note that the grooves produce a negligible effect on the rupture propagation, as shown in Supplementary Fig.  2a . Furthermore, the strain measurements and their correspondence to LEFM at x  = 100 mm (with grooves, Supplementary Fig.  1c ) and x  = 140 mm (without grooves, Supplementary Fig.  2b ) show that both the grooved and non-grooved locations have the same fracture energy. While the grooves redistribute the contact area at the micro-scale within the interface (e.g., the local contact density increases at groove edges and is zero within the grooves), this does not influence the macro-scale rupture properties (i.e., the nominal stress distribution millimeters away from the interface or the propagation speeds).

We note in the main text that, during the first 5 μs, both blocks show the same positive displacement. One possible explanation for these displacements is that they are caused by local material rotational deformation under the action of amplified shear stresses by the approaching singularity.

Determining the propagation speed of secondary ruptures

Differentiation of the contact area, \(\overline{{\partial }_{t}A\left(x,\, t\right)}\) , highlights the contact area changes induced by weak secondary ruptures. To detect the propagation velocities, \({C}_{{{{{{\rm{f}}}}}}},\,\) of these weak fronts, we first convert the \(\overline{{\partial }_{t}A\left(x,\, t\right)}\) maps (e.g., Fig.  2a ) to contour plots. These contours produce ridges along the \(x,\, t\) paths that the rupture fronts trace. \({C}_{{{{{{\rm{f}}}}}}}\) is determined by performing a linear fit to this ridge. Some examples of this procedure are presented in Supplementary Fig.  5 . In these examples we illustrate the i  = 1st, 4th, and 9th rupture fronts presented in Fig.  2e . Secondary rupture speeds of the secondary rupture sequence described in Fig.  2 are listed in Supplementary Table  1 . A portion of the secondary ruptures are so weak that we can not reliably detect their speeds. These rupture speeds are left undetermined in Supplementary Table  1 .

Fracture energy

The initial fracture energy Γ 1 is determined by the interface contact quality, which is influenced by the normal loading force, the static aging time from imposition of \({F}_{{{{{{\rm{N}}}}}}}\) until the initiation of the first rupture, and the surface’s roughness 42 , 43 . In our experiments, Γ 1 was obtained from fitting the slip profiles to LEFM predictions 28 , 45 . The value corresponds well to the corresponding strain gage measurements 4 (see Supplementary Fig.  1c ) and yield Γ 1  = 1.3 J m –2 .

The secondary ruptures occur along the same interface as the first rupture, but the fracture energies, Γ i will vary widely as a result of the variation of the intervals, \(\Delta {t}_{i}\) , between the initiation of the i – 1 and the i th ruptures. \(A(t)\) , hence \({\varGamma }_{i}\) increase approximately logarithmically 5 , 44 with \(\Delta {t}_{i}\) . Since σ yy is constant throughout each rupture sequence, Γ i will scale with the contact drop δ A i in the immediate wake of each rupture. Using the i  = 1 rupture as a baseline, Γ i can be estimated via Γ i  =  Γ 1 · ( δA i / δA 1 ). The fracture energies of the rupture sequence presented in Fig.  2 are listed in Supplementary Table  1 .

LEFM with a cohesive zone model

Sub-rayleigh ruptures.

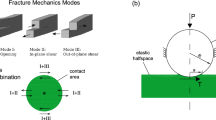
Within the fracture mechanics framework, the propagation of rupture fronts is well-described by the LEFM solution for sub-Rayleigh shear cracks (Model II). The stresses in the vicinity of the rupture tip are predominantly described by

where ( r , θ ) are polar coordinated with respect to the rupture tip, \({\Sigma }_{{ij}}^{{{{{{\rm{II}}}}}}}({\theta },\, {C}_{{{{{{\rm{f}}}}}}})\) are known universal functions for the angular dependence of each component and the scalar K II is the stress intensity factor 45 . This singular LEFM solution, which predicts infinite stresses at the rupture tip, is renormalized within a dissipative region located at the crack tip. This region, where the material strength is limited by τ p , is commonly referred to as the cohesive zone or process zone 45 .

As illustrated in Supplementary Fig.  1a , a direct measure of the characteristic size of the cohesive zone can be determined by the spatial scale, X c , over which the contact area drops at a rupture tip 4 . Examples of renormalized contact area in space for two typical ruptures, both rapid 0.99 C R and slow 0.02 C R , are presented in Supplementary Fig.  1a . X c , decreases as \({C}_{{{{{{\rm{f}}}}}}}\to {C}_{{{{{{\rm{R}}}}}}}\) to zero, an effective ‘Lorentz’ contraction’ described by fracture mechanics \({{X}_{c}=X}_{c}^{0}/{f}_{{{{{{\rm{II}}}}}}}({C}_{{{{{{\rm{f}}}}}}})\) , where \({f}_{{{{{{\rm{II}}}}}}}({C}_{{{{{{\rm{f}}}}}}})\) is a known universal function 45 . The examples in Supplementary Fig.  1a demonstrate contraction, while Supplementary Fig.  1b demonstrates that this general result of elastodynamic theory (black line) describes the measurements (points) well.

We now make the assumption that \({X}_{c}\) is independent of Γ , and is given by the above expression. Using the measured values of \({\varGamma }_{i}\) and \({X}_{c}^{0}\) and assuming shear stress weakening within the cohesive zone 47 as \({\tau }(x)=({{\tau }}_{{{{{{\rm{p}}}}}}}{-}{{\tau }}_{{{{{{\rm{r}}}}}}}) \cdot \, \widetilde{\tau }((x-{x}_{{{{{{\rm{tip}}}}}}}\left)\right./{X}_{c}))+{{\tau }}_{{{{{{\rm{r}}}}}}}\) , where \(\widetilde{\tau }\left({\xi }\right)={e}^{{\xi }}\) , we can estimate the elusive constitutive parameters that define the dissipative processes and material properties under the extreme conditions near the rupture tip. The peak shear strength τ p can be directly inferred using the following expression 28 , 48 :

where \(\widetilde{G}\left({C}_{{{{{{\rm{f}}}}}}},\, \widetilde{\tau }\left({\xi }\right)\right)={f}_{{{{{{\rm{II}}}}}}}\left({C}_{{{{{{\rm{f}}}}}}}\right){[{\int }_{-{\infty }}^{0}\frac{\widetilde{\tau }\left({\xi }\right)}{\sqrt{-{\xi }}}d{\xi }]}^{2}\) . Here, τ r and μ are, respectively, the residual stress along the interface and shear modulus, k  = C S /C L . Strain and stress can be obtained, as well as the slip function u x , by calculating explicitly the dynamic fields 28 . We note that this model differs slightly from that used in ref. 28 , where ruptures propagated with different speeds but had a constant Γ (or constant peak shear strength τ p ) 28 . Here the fracture energy (or peak shear strength) utilized is the value \({\varGamma }_{i}\) that is produced by the contact area drop of each secondary rupture. More details of the model can be found in ref. 28 .

Supershear ruptures

Supershear ruptures are very prevalent secondary ruptures. In the case of supershear cracks, stress fields ahead of the tip are only coupled to the system’s longitudinal waves. These create a singularity at the crack tip which can be described by \({{\sigma }}_{{ij}} \sim 1/{r}^{g}\) 49 . The singular exponent g depends strongly on the crack speed ( g ( C f ) ≤ 1/2), an effect notably different from sub-Rayleigh cracks. To compare the measured strain profiles with fracture mechanics predictions, we extend the sub-Rayleigh cohesive zone model directly to the supershear regime. The regularization of the shock wave singularity arises naturally when a cohesive zone is introduced, as it effectively regulates the stress divergences at the crack tip 28 . Details of the model can be found in ref. 28 .

Comparison between LEFM and experiments

For comparison of LEFM to the strain gauge signals (Fig.  3d ), we determine the strain variations, \(\delta {\varepsilon }_{{ij}}\) , due to each rupture passage by using the peak strain variations within a \(10\) μs time window on either side of a rupture’s passage. This window is necessary to compensate for any uncertainty in the precise arrival time of each (weak) rupture, as these variations mainly result 4 from the angular function \({\Sigma }_{{ij}}^{{{{{{\rm{II}}}}}}}({\theta },\, {C}_{{{{{{\rm{f}}}}}}})\) .

Undetected ruptures

The roll-off at the left-top as shown in the inset of Fig.  4b may be an indication that ruptures with slips smaller than 3 µm are only partially detected. For example, in the interval between the 8th to 9th ruptures that were labeled in Fig.  2b , it is possible to observed a number of additional shallow ruptures. During this period, the contact area does not increase monotonically (as would be expected from aging after the cessation of slip). \(A\left(x,\, t\right)\) is, instead, essentially flat with small fluctuations. This indicates a weakening of the contact interface induced by secondary ruptures which are nearly below our detection threshold.

Estimation of the seismic moment for secondary ruptures

When calculating the seismic moment, the two key inputs are the mean slip and the area within a fault where slip takes place. In our experiment, it is challenging to precisely calculate the seismic moment: \({M}_{0(i)}={\int }_{0}^{L}{GW}{{\delta }u}_{x(i)}(x){dl}\) , since we do not know the slip distribution along the whole interface. To estimate \({M}_{0(i)}\) we simplified the calculation by using \({M}_{0(i)}\,{{{{\approx }}}}\,G{\cdot }W{\cdot }{{\delta }u}_{i}L=\) \(G{\cdot }S{\cdot }{{\delta }u}_{i}\) , where S  =  WL the entire interface area (since the secondary ruptures generally traverse the entire interface). With this simplification, the seismic moments of the secondary ruptures vary from 1 to 50 N·m. The magnitudes of these lab-earthquakes are, therefore, close to – 5, based on the formula 2/3(log M 0 – 9.1) 50 .

Data availability

The experimental data 51 generated in this study have been deposited in the Zenodo database under access code https://doi.org/10.5281/zenodo.10073589 .

Brace, W. F. & Byerlee, J. D. Stick-slip as a mechanism for earthquakes. Science 153 , 990–992 (1966).

Article   ADS   CAS   PubMed   Google Scholar  

Scholz, C. H. Earthquakes and friction laws. Nature 391 , 37–42 (1998).

Article   ADS   CAS   Google Scholar  

Gvirtzman, S. & Fineberg, J. Nucleation fronts ignite the interface rupture that initiates frictional motion. Nat. Phys. 17 , 1037–1042 (2021).

Article   CAS   Google Scholar  

Svetlizky, I. & Fineberg, J. Classical shear cracks drive the onset of dry frictional motion. Nature 509 , 205–208 (2014).

Ben-David, O., Rubinstein, S. M. & Fineberg, J. Slip-stick and the evolution of frictional strength. Nature 463 , 76–79 (2010).

Rubinstein, S. M., Cohen, G. & Fineberg, J. Detachment fronts and the onset of dynamic friction. Nature 430 , 1005–1009 (2004).

Rice, J. R. & Ruina, A. L. Stability of steady frictional slipping. J. Appl. Mech . 50 , 343–349 (1983).

Tullis, T. E. & Weeks, J. D. Constitutive behavior and stability of frictional sliding of granite. Pure Appl. Geophys. 124 , 383–414 (1986).

Article   ADS   Google Scholar  

Gutenberg, B. & Richter, C. F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34 , 185–188 (1944).

Article   Google Scholar  

Jiang, J., Bock, Y. & Klein, E. Coevolving early afterslip and aftershock signatures of a San Andreas fault rupture. Sci. Adv. 7 , eabc1606 (2021).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Perfettini, H., Frank, W. B., Marsan, D. & Bouchon, M. A model of aftershock migration driven by afterslip. Geophys. Res. Lett. 45 , 2283–2293 (2018).

Passelègue, F. X., Schubnel, A., Nielsen, S., Bhat, H. S. & Madariaga, R. From sub-Rayleigh to supershear ruptures during stick-slip experiments on crustal rocks. Science 340 , 1208–1211 (2013).

Article   ADS   PubMed   Google Scholar  

Kanamori, H. & Brodsky, E. E. The physics of earthquakes. Rep. Prog. Phys. 67 , 1429–1496 (2004).

Article   ADS   MathSciNet   Google Scholar  

Ke, C. Y., McLaskey, G. C. & Kammer, D. S. Earthquake breakdown energy scaling despite constant fracture energy. Nat. Commun. 13 , 1005 (2022).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Cocco, M. et al. Fracture energy and breakdown work during earthquakes. Annu. Rev. Earth Planet. Sci . 51 , 217–252 (2023).

Kammer, D. S. & McLaskey, G. C. Fracture energy estimates from large-scale laboratory earthquakes. Earth Planet. Sci. Lett. 511 , 36–43 (2019).

Ben-David, O., Cohen, G. & Fineberg, J. The dynamics of the onset of frictional slip. Science 330 , 211–214 (2010).

Bayart, E., Svetlizky, I. & Fineberg, J. Fracture mechanics determine the lengths of interface ruptures that mediate frictional motion. Nat. Phys. 12 , 166–170 (2015).

Svetlizky, I., Kammer, D. S., Bayart, E., Cohen, G. & Fineberg, J. Brittle fracture theory predicts the equation of motion of frictional rupture fronts. Phys. Rev. Lett. 118 , 125501 (2017).

Ohnaka, M. & Kuwahara, Y. Characteristic features of local breakdown near a crack-tip in the transition zone from nucleation to unstable rupture during stick-slip shear failure. Tectonophysics 175 , 197–220 (1990).

Rubino, V., Rosakis, A. J. & Lapusta, N. Understanding dynamic friction through spontaneously evolving laboratory earthquakes. Nat. Commun. 8 , 15991 (2017).

Okubo, P. G. & Dieterich, J. H. Fracture energy of stick-slip events in a large scale biaxial experiment. Geophys. Res. Lett. 8 , 887–890 (1981).

Paglialunga, F. et al. On the scale dependence in the dynamics of frictional rupture: constant fracture energy versus size-dependent breakdown work. Earth Planet. Sci. Lett . 584 , 117442 (2022).

Passelègue, F. X. et al. Dynamic rupture processes inferred from laboratory microearthquakes. J. Geophys. Res. Solid Earth 121 , 4343–4365 (2016).

Chen, X., Chitta, S. S., Zu, X. & Reches, Z. Dynamic fault weakening during earthquakes: Rupture or friction? Earth Planet. Sci. Lett. 575 , 117165 (2021).

Mclaskey, G. C. & Yamashita, F. Slow and fast ruptures on a laboratory fault controlled by loading characteristics. J. Geophys. Res. Solid Earth 122 , 3719–3738 (2017).

Berman, N., Cohen, G. & Fineberg, J. Dynamics and properties of the cohesive zone in rapid fracture and friction. Phys. Rev. Lett. 125 , 125503 (2020).

Svetlizky, I., Albertini, G., Cohen, G., Kammer, D. S. & Fineberg, J. Dynamic fields at the tip of sub-Rayleigh and supershear frictional rupture fronts. J. Mech. Phys. Solids 137 , 103826 (2020).

McLaskey, G. C., Kilgore, B. D. & Beeler, N. M. Slip‐pulse rupture behavior on a 2 m granite fault. Geophys. Res. Lett. 42 , 7039–7045 (2015).

Xu, S. et al. Strain rate effect on fault slip and rupture evolution: insight from meter-scale rock friction experiments. Tectonophysics 733 , 209–231 (2018).

Xu, S., Fukuyama, E., Yamashita, F. & Takizawa, S. Evolution of fault-interface Rayleigh Wave speed over simulated earthquake cycles in the lab: observations, interpretations, and implications. Earth Planet. Sci. Lett. 524 , 115720 (2019).

Fryer, B. et al. The influence of roughness on experimental fault mechanical behavior and associated microseismicity. J. Geophys. Res. Solid Earth 127 , e2022JB025113 (2022).

Heaton, T. H. Evidence for and implications of self-healing pulses of slip in earthquake rupture. Phys. Earth Planet. Inter. 64 , 1–20 (1990).

Li, Q., Tullis, T. E., Goldsby, D. & Carpick, R. W. Frictional ageing from interfacial bonding and the origins of rate and state friction. Nature 480 , 233–236 (2011).

Ryan, K. L., Rivière, J. & Marone, C. The role of shear stress in fault healing and frictional aging. J. Geophys. Res. Solid Earth 123 , 10,479–10,495 (2018).

Andrews, D. J. Rupture velocity of plane strain shear cracks. J. Geophys. Res. 81 , 5679–5687 (1976).

Burridge, R. Admissible speeds for plane-strain self-similar shear cracks with friction but lacking cohesion. Geophys. J. Int. 35 , 439–455 (1973).

Xia, K., Rosakis, A. J. & Kanamori, H. Laboratory earthquakes: the sub-Rayleigh-to-supershear rupture transition. Science 303 , 1859–1861 (2004).

Zhan, Z., Helmberger, D. V., Kanamori, H. & Shearer, P. M. Supershear rupture in a Mw 6.7 aftershock of the 2013 Sea of Okhotsk earthquake. Science 345 , 204–207 (2014).

Dunham, E. M., Favreau, P. & Carlson, J. M. A supershear transition mechanism for cracks. Science 299 , 1557–1559 (2003).

Xu, S. et al. Fault strength and rupture process controlled by fault surface topography. Nat. Geosci. 16 , 94–100 (2023).

Rubinstein, S. M., Cohen, G. & Fineberg, J. Contact area measurements reveal loading-history dependence of static friction. Phys. Rev. Lett. 96 , 256103 (2006).

Svetlizky, I., Bayart, E., Cohen, G. & Fineberg, J. Frictional resistance within the wake of frictional rupture fronts. Phys. Rev. Lett. 118 , 234301 (2017).

Chaves, E. J., Schwartz, S. Y. & Abercrombie, R. E. Repeating earthquakes record fault weakening and healing in areas of megathrust postseismic slip. Sci. Adv. 6 , eaaz9317 (2020).

Freund, L. B. Dynamic fracture mechanics . (Cambridge university press, 1998).

Dalbe, M. J., Cortet, P. P., Ciccotti, M., Vanel, L. & Santucci, S. Multiscale stick-slip dynamics of adhesive tape peeling. Phys. Rev. Lett. 115 , 128301 (2015).

Palmer, A. C., Rice, J. R. & Hill, R. The growth of slip surfaces in the progressive failure of over-consolidated clay. Proc. R. Soc. Lond. Math. Phys. Sci. 332 , 527–548 (1973).

ADS   Google Scholar  

Samudrala, O., Huang, Y. & Rosakis, A. J. Subsonic and intersonic shear rupture of weak planes with a velocity weakening cohesive zone. J. Geophys. Res. Solid Earth 107 , ESE 7-1–ESE 7-32 (2002).

Broberg, K. B. Cracks and fracture . (Elsevier, 1999).

Hanks, T. C. & Kanamori, H. A moment magnitude scale. J. Geophys. Res. 84 , 2348 (1979).

Songlin, S. How frictional slip evolves. Zenodo https://doi.org/10.5281/zenodo.10073589 (2023).

Download references

Acknowledgements

We thank M. Adda-Bedia (ENS Lyon) and D. Kammer (ETH Zurich) for helpful discussions. This work was supported by Israel Science Foundation, grant numbers 840/19.and 416/23. S.S. acknowledges the support of the Emily Erskine Endowment Fund. M.W. acknowledges the support of the Lady Davis Fellowship Trust.

Author information

Authors and affiliations.

The Racah Institute of Physics, The Hebrew University of Jerusalem, Givat Ram, Jerusalem, 91904, Israel

Songlin Shi, Meng Wang, Yonatan Poles & Jay Fineberg

You can also search for this author in PubMed   Google Scholar

Contributions

S.S. and J.F. conceived of the project. S.S. designed and performed research with help of M.W and Y.P. S.S and J.F. analyzed the results. S.S. and J.F. wrote the manuscript. J.F. supervised the research. All authors discussed the results and commented on the manuscript.

Corresponding author

Correspondence to Jay Fineberg .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Peer review

Peer review information.

Nature Communications thanks Antonio Papangelo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Peer review file, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Shi, S., Wang, M., Poles, Y. et al. How frictional slip evolves. Nat Commun 14 , 8291 (2023). https://doi.org/10.1038/s41467-023-44086-1

Download citation

Received : 25 July 2023

Accepted : 28 November 2023

Published : 14 December 2023

DOI : https://doi.org/10.1038/s41467-023-44086-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Earthquake energy dissipation in a fracture mechanics framework.

• David S. Kammer
• Gregory C. McLaskey
• Elisa Tinti

Nature Communications (2024)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Stick-Slip Movement

A lesson form FEMA/AGU earthquake curriculum for teachers of grades 7-12.

This section is intended to help students observe how stick-slip movement works. Instructions on how to build a motorized version of the following experiment as well as data produced from this model are available.

Motorized version

"Can Earthquakes Be Predicted?" Some background information

Activities page

What Happens When the Earth Quakes?

In this unit students will move beyond their own personal survival and that of their community, the focus of Unit 1, to the big picture of earthquakes in space and time. Since the Seismic Sleuths curriculum is intended to supplement, and not to replace, your school’s own syllabus, it sketches this big picture without filling in all the basic earth science background. Your preparation to teach these lessons must begin with an assessment of your students’ readiness. If they have no familiarity with rocks and minerals or with faulting and other processes that form landscapes, you may need to provided a brief introduction from the first few chapters of a high school geology or earth science textbook.

Unit 2 begins with a hands-on activity that models what happens when the stresses accumulated at a fault are released in an earthquake. Using a box, a board, sandpaper, and other simple materials, students apply scientific method and basic math skills to measure movement, calculate averages, and plot their information on a graph.

The second lesson includes three activities and an overview of what is now known about Earth’s ever-shifting surface and its layered inner structure. In the first activity, students will reproduce the magnetic evidence for the migration of Earth’s poles in the course of tectonic movement. In the second, they see how this record is written in the rocks at mid-ocean ridges. In the third, they create a map showing the arrangement of the continents 120 million years ago, and compare it with the map of the world today. As students consider several alternative explanations for tectonic plate movement, remind them that earth science, like the Earth it studies, is constantly in motion. Scientific knowledge moves forward through questioning and the development of hypotheses into theories; its goal is never to provide dogmatic answers.

The third lesson begins with an exercise in which students contrast the small scope of historic time with the vastness of geologic time. In the second activity, Paleoseismology, they simulate the techniques seismologists use to read the record of relatively recent earthquakes.

The amount of damage an earthquake causes depends on the strength and duration of the earthquake, on population density, on methods of construction (to be dealt with in Unit 4), and on the geophysical/geological characteristics of the impacted area. Lesson 4 progresses to three of the most potentially destructive earthquake effects: liquefaction, landslides, and tsunami. Each occurs when a seismic shock impacts an area with certain physical characteristics. Lesson 5 underlines the importance of site, as students interpret maps highlighting different features of the landscape. They will draw on their new knowledge to make additions to the local map they began in Unit 1.    

Students will operate a model to observe the type of motion that occurs at a fault during an earthquake and explore the effects of several variables.

Focus Questions

How much energy will a fault store before it fails?

Is this quantity constant for all faults?

Students will:

For each small group

Teacher Preparation

To assure success, construct the model ahead of time and rehearse the activity. Then arrange materials for student models in a convenient place.

Created By Dave Love, Chris Durand and John Van Der Kamp

last modified: 25 April, 2022

An Experimental Study on Adhesion, Friction and Stick-Slip Phenomena

• Conference paper
• First Online: 31 July 2019
• Cite this conference paper

• Arun K. Singh 6 ,
• Avinash A. Thakre 6 &
• Nitish Sinha 6  

Part of the book series: Lecture Notes in Mechanical Engineering ((LNME))

1534 Accesses

Stick-slip vibration is an important mode of failure in many structural and mechanical systems and that generally seen in the form of jerking, chattering, squeaking, etc. It is shown experimentally that similar to friction, adhesion is also dynamic in nature and that depends on slip velocity and relaxation or hold time. Fracture mechanics analysis of a soft and hard solid interface in the direct shear sliding reveals that energy release rate ( ERR ) varies periodically during stick-slip motion. However, in the steady sliding regime, ERR first increases to a maximum value at static strength, becomes constant during dynamic sliding and finally, the ERR reaches at the residual strength to a constant value known as work of adhesion. It is also observed during stick-slip motion that a crack always nucleates from the rear end of the block and traverses the entire interface before the slip and is followed by healing of the same interface begins from the front edge of the block. The present study establishes that a relative competition between the crack growth rate and interface healing rate basically controls the frictional behavior of sliding surfaces.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

The effect of dynamic normal force on the stick–slip vibration characteristics

On the Degree of Irreversibility of Friction in Sheared Soft Adhesive Contacts

Creep to inertia dominated stick-slip behavior in sliding friction modulated by tilted non-uniform loading

B.N.J. Persson, Friction of elastic solids (Springer, Heidelberg, 2002)

Google Scholar  

R.A. Ibrahim, Appl. Mech. Rev. 47 , 209 (1994)

Article   Google Scholar  

J.R. Rice, A.L. Ruina, J. Appl. Mech. 50 , 343 (1983)

E. Rabinowicz, Proc. of the Phys. Soc. 71 (4), 668 (1958)

A. Ruina, J. Geophys. Res.: Solid Earth 88 , 10359 (1983)

T. Baumberger, C. Caroli, O. Ronsin, Euro. Phys. J. E 11 , 85 (2003)

T. Yamaguchi, S. Ohmata, M. Doi, J. Phys.: Condens. Mat. 21 , 205105 (2009)

A.D. Berman, W.A. Ducker, J.N. Israelachvili, Langmuir 12 , 4559 (1996)

A.E. Filippov, J. Klafter, M. Urbakh, Phys. Rev. Lett. 92 , 135503 (2004)

A.K. Singh, V.A. Juvekar, Soft Matter 7 , 10601 (2011)

A.K. Singh, V.A. Juvekar, arXiv preprint arXiv:1412.0099 , (2014)

V. Gupta, A.K. Singh, Int. J. Mod. Phys. B 30 , 1650198 (2016)

S.M. Rubinstein, M. Shay, G. Cohen, J. Fineberg 140 , 201 (2006)

O. B. David, S.M. Rubinstein, Nature, 463 (2010), 76–79 (2010)

I. Svetlizky, J. Fineberg, Nature 509 (7499), 205 (2014)

A.A. Thakre, A.K. Singh, J. Adhes. Sci. Tech. 32 , 1899 (2018)

A.A. Thakre, A.K. Singh, Mat. Res. Exp. 5 (8), (2018)

A.A. Thakre, Ph.D thesis, VNIT Nagpur (2018)

A.A. Griffith, Proc. Royal Soc. Lond. 221 , 582 (1921)

D. Maugis, Contact (Adhesion and Rupture of elastic solids, Springer, Heidelberg, 2000)

MATH   Google Scholar  

Download references

Acknowledgements

The authors wish to acknowledge the MHRD, Government of India for granting funds under TEQIP-II to establish the experimental facility at VNIT Nagpur for the present study.

Author information

Authors and affiliations.

Department of Mechanical Engineering, VNIT, Nagpur, 440010, Maharashtra, India

Arun K. Singh, Avinash A. Thakre & Nitish Sinha

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Arun K. Singh .

Editor information

Editors and affiliations.

Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai, Tamil Nadu, India

Raghu V. Prakash

Reactor Design Group, Indira Gandhi Centre for Atomic Research, Kalpakkam, Tamil Nadu, India

R. Suresh Kumar

Materials Development and Technology Division, Indira Gandhi Centre for Atomic Research, Kalpakkam, Tamil Nadu, India

Atikukke Nagesha

Gomathy Sasikala

Indira Gandhi Centre for Atomic Research, Kalpakkam, Tamil Nadu, India

Arun Kumar Bhaduri

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Singapore Pte Ltd.

About this paper

Cite this paper.

Singh, A.K., Thakre, A.A., Sinha, N. (2020). An Experimental Study on Adhesion, Friction and Stick-Slip Phenomena. In: Prakash, R., Suresh Kumar, R., Nagesha, A., Sasikala, G., Bhaduri, A. (eds) Structural Integrity Assessment. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-13-8767-8_49

Download citation

DOI : https://doi.org/10.1007/978-981-13-8767-8_49

Published : 31 July 2019

Publisher Name : Springer, Singapore

Print ISBN : 978-981-13-8766-1

Online ISBN : 978-981-13-8767-8

eBook Packages : Engineering Engineering (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

We apologize for the inconvenience...

To ensure we keep this website safe, please can you confirm you are a human by ticking the box below.

If you are unable to complete the above request please contact us using the below link, providing a screenshot of your experience.

https://ioppublishing.org/contacts/

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Peer-reviewed

Research Article

Experimental analysis of the stick-slip characteristics of faults at different loading rates

Roles Writing – original draft

* E-mail: [email protected]

Affiliations School of Civil Engineering, Liaoning Technical University, Fuxin, Liaoling, China, Institute of Geology, China Earthquake Administration, Beijing, China

Roles Data curation, Formal analysis, Writing – review & editing

Affiliation School of Civil Engineering, Liaoning Technical University, Fuxin, Liaoling, China

Roles Resources

Affiliation College of Resources & Safety Engineering, China University of Mining & Technology, Beijing, China

Roles Writing – review & editing

• Bao-xin Jia, 
• Zong-xian Gao, 
• Xiu-hui Han, 
• Jia-xu Jin, 
• Jian-jun Zhang

• Published: April 24, 2020
• https://doi.org/10.1371/journal.pone.0231464
• Peer Review
• Reader Comments

In deep underground engineering, in a large spatial, high-stress environment, rapid excavation is likely to affect the loading rate of the fault structure and to cause stick-slip. In this study, an experiment was conducted to explore the stick-slip characteristics at different loading rates. A double-sided shear experiment and the digital speckle correlation method were used to analyze the evolution of the displacement field, the slip displacement, and the slip rate of the fault’s stick-slip activity at different loading rates as well as their correlation with the loading rate. The loading rate, moment magnitude, and stress drop of the fault’s stick-slip and their corresponding relationships were studied. The results show that the occurrence of stick-slip is inversely proportional to the loading rate. The evolution of the fault-slip displacement field at different loading rates is similar. At a given loading rate, the magnitude is positively correlated with the stress drop. The magnitude and stress drop are inversely related to the loading rate.

Citation: Jia B-x, Gao Z-x, Han X-h, Jin J-x, Zhang J-j (2020) Experimental analysis of the stick-slip characteristics of faults at different loading rates. PLoS ONE 15(4): e0231464. https://doi.org/10.1371/journal.pone.0231464

Editor: Peitao Wang, University of Science and Technology Beijing, CHINA

Received: January 1, 2020; Accepted: March 24, 2020; Published: April 24, 2020

Copyright: © 2020 Jia et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: All relevant data are within the paper.

Funding: This work was supported by The National Natural Science Foundation of China (No. 51774173), the Natural Science Foundation of Liaoning Province (No. 201602351), and the Open Fund for the State Key Laboratory of Seismological Dynamics (No. LED2015B01) to BJ. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Competing interests: The authors have declared that no competing interests exist.

List of symbols: G, The shear modulus of the rock; D, The stick-slip displacement; A, The area of the slip surface of the fault; M 0 , The seismic moment; M w , The moment magnitude; Δ σ , The actual stress drop; Δ σ V , The total stress drop; T, The time of sudden displacement change during stick-slip; t V , The time of the actual stress drop

Introduction

As basic and common geological structures, faults are widely found in underground engineering. The slippage of faults is a common phenomenon of rock friction and can be divided into two different phenomena: smooth and sticky. Fault-slips are characterized by a two-disc lockout of the fault, and the stress continuously accumulates. When the stress reaches or exceeds the friction between the two plates, the fault suddenly slides, producing relative displacement and relieving stress. During recent years, as China’s geotechnical engineering construction, e.g., mining resources, underground storage facilities, water conservancy, and hydropower, has gradually developed in deep underground and high stress areas, accidents such as roof collapse, landslides, water inrush, and impact ground pressure caused by engineering-induced fault slips have increased. Therefore, in-depth research on fault slip characteristics is of important practical significance for the prediction, prevention, and control of disasters in geotechnical engineering [ 1 , 2 , 3 , 4 , 5 ]

Fault slips are one of the hot topics worldwide in the field of seismic and geotechnical engineering, and numerous studies have been carried out. [ 6 ] conducted stick-slip experiments based on three structural models to explore the relationship between the type of stick-slip, the stress drop, and the magnitude. [ 7 ] studied the entire process of fault evolution from stable sliding to stick-slip. [ 8 ] explored the slow fault-slip mechanism through laboratory observations. In addition, [ 9 ] conducted a double-sided shear experiment to analyze the evolution characteristics of fault displacement during inter-slip periods and stick-slip periods. [ 10 ] studied the dynamic response of geological materials to acceleration, velocity, and displacement during fracturing and slippage under laboratory conditions. Furthermore, [ 11 ] established a discrete element model to simulate a single fault biaxial sliding test and used it to investigate the effects of rock particle elasticity, friction coefficient, fault stiffness, and normal stress on fault evolution. [ 12 ] conducted a dynamic direct shear test to study the effects of surface roughness and normal stress on the rock joint friction coefficient and micro-shear deformation mechanism. Through a similarity model experiment, [ 13 ] explored the movement law of the overburden strata under mining influences and the evolution of fault stress and analyzed the mechanism of fault reactivation caused by coal seam mining. In terms of theoretical research, based on gradient-dependent plasticity, [ 14 ] obtained the theoretical expression for the relative displacement of the fault zone along the observed trend. Based on a mechanical model of the stick-slip of a coal body relative to the top and bottom plates, [ 15 ] investigated the conditions of coal stick-slip and established a dynamic equation for the coal body after the occurrence of stick-slip. [ 16 ] studied the movement law of the double-slider system under different coupling stiffness conditions, obtaining the sliding mode of the slider system under strong and weak coupling conditions. In terms of numerical computations, [ 17 ] used the Lagrangian element method to study the influence of the loading rate on the stress level, the plastic zone size, and the snap-back characteristics of the fault band and elastic rock system. In addition, [ 18 ] used the Coulomb shear model to study the spatial and temporal evolutions of the normal stress and shear stress on the fault contact surface in the mining process as well as the movement law of the upper wall and footwall of the faults. According to micro-seismic mine data, [ 19 ] performed a back analysis of fault slip data using a three-dimensional numerical simulation of the entire well, obtaining the physical and mechanical properties of the shear band.

Although significant achievements have been made in fault slip research, deep underground engineering construction involving high-stress environments, the exploitation of large spaces, and rapid construction has been increasing in recent years. First, fault stick-slip is likely to occur in a high-stress environment. Second, exploitation of large spaces and rapid construction may cause a loading rate effect of the fault structure. Therefore, with respect to the influence of the loading rate on fault stick-slip, considerable and intense experimental research still needs to be performed to provide further experimental support for establishing theoretical models and for conducting numerical simulation of geotechnical engineering projects influenced by fault structures in deep underground or high-stress environments.

In this study, we use digital image correlation methods to accurately measure the deformation and displacement of rock specimens [ 20 , 21 , 22 ]. A charge-coupled device (CCD) camera and a high-speed camera were used to build an image acquisition system. Through analysis of the speckle field on the surface of the collected specimens using the digital speckle correlation method, a double-sided shear experiment was carried out to study the evolution characteristics of the displacement field, the slip displacement, the loading curve, the slip rate, the magnitude, and the stress drop of fault stick-slip at different loading rates.

Materials and methods

In this study, a double-sided shear experiment was conducted to explore the evolutionary characteristics of the fault stick-slip at different loading rates. Fig 1 shows the dimensions, displacement boundaries, and loading conditions of the specimens. The rock material was granite with a shear modulus of approximately 25.7 GPa. The specimens used in the fault stick-slip experiment were three pieces of granite, including two fixed rock blocks and one sliding rock block. The dimensions of the fixed rocks was 300 mm × 50 mm × 50 mm (L × W × H), and those of the sliding block was 350 mm × 50 mm × 100 mm. The specimens consisted of two sliding surfaces (Sliding surface 1 and Sliding surface 2), the area of which was 0.015 m 2 (300 mm × 50 mm). The sliding surfaces were polished using 300# emery paper, and the artificial speckle field was sprayed on the observation surface of the model.

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

https://doi.org/10.1371/journal.pone.0231464.g001

The displacement boundary and loading conditions of the specimens were as follows. The horizontal displacement on the left side of the two fixed rocks was restricted, and the horizontal displacement on the right side was kept in a free state. Considering the actual stress state of the fault and the compressive strength of the rock specimen and based on the setting of the normal stress used in previous shear tests [ 23 , 24 ], a constant vertical pressure of 25 MPa was selected to create stick-slip conditions. The left side of the sliding block was kept in a free state, and the right side was loaded using the displacement control loading method. According to the variation range of the displacement of the mining project, 18 experiments with 6 loading rates were designed and conducted (three experiments for each loading rate). The loading rates were 4 μm/s, 6 μm/s, 8 μm/s, 10 μm/s, 15 μm/s, and 20 μm/s.

The experimental system consisted of two parts, i.e., the loading device and the image acquisition system. Fig 2 shows the setup of the experimental system. The experimental loading device was a RLJW-2000 hydraulic servo testing machine with a maximum axial load of 3000 kN and a maximum horizontal load of 1500 kN. The data recording frequency range of the loading device was 1×10 −5 to 30 Hz; and the strain loading rate was 1×10 −7 to 1×10 −2 mm/s. The image acquisition system included a CCD camera, a high-speed camera, and a high-speed camera trigger device. CCD is the most commonly used image sensor for machine recording. In this experiment, the model of the CCD camera used was acA1600-20gm. The CCD camera was used to collect the speckle images on the surface of the specimens throughout the process, with an acquisition rate of 5 frames per second and an object surface resolution of 0.20 mm per pixel. The high-speed camera was an industrial digital camera, which converted digital image capture targets into image signals and sent them to a dedicated image processing system. The image system performed various operations on these signals to extract the features of the targets. The high-speed camera model used in this experiment was a Photron Fast Cam SA1.1. The high-speed camera was responsible for collecting images of the surface of the specimens during the transient process of the fault stick-slip motion. With the high-decibel sound emitted by the fault stick-slip as the triggering condition, the post-trigger mode was adopted with an acquisition rate of 4000 frames per second and an object surface resolution of 0.50 mm per pixel.

https://doi.org/10.1371/journal.pone.0231464.g002

Prior to the experiments, the time of the loading device and that of the image acquisition system were synchronized, and the image acquisition system was debugged. During the experiments, a vertical load was applied to the specimens and remained constant once it reached 25 MPa, which was the preset value. Then, the CCD camera and the high-speed camera were used simultaneously to capture the speckle images on the surface of the specimens as reference images for the digital speckle correlation method. Finally, in the displacement control-loading mode, the specimens were loaded horizontally at the designated loading rate. In addition, the CCD camera was used to collect the speckle images on the surface of the specimens throughout the process, and the high-speed camera was activated by the post-trigger mode to acquire the speckle images on the surface of the specimens during each fault stick-slip motion until the end of the experiments.

Results and discussion

Characteristics of the stress evolution of the fault stick-slip at different loading rates.

Fig 3 shows the typical loading curves for the six predefined loading rates. To better display the loading curves, only the first three stick-slip processes are presented. Table 1 shows the values of the stress drops corresponding to the results in Fig 3 , where the marked points correspond to the analysis time of the displacement field. As shown in the Fig 3 and Table 1 , the starting time of the first stick-slip of the specimens decreased as the loading rate increased, and the time it took for the stick-slip to occur decreased with increasing loading rate. The shear stress of the first stick-slip was 12.55–14.43 MPa, and the stress drop varied from 0.23 MPa to 1.14 MPa, indicating an insignificant correlation between the shear stress and the stress drop of the first stick-slip and the loading rate.

https://doi.org/10.1371/journal.pone.0231464.g003

https://doi.org/10.1371/journal.pone.0231464.t001

The shear stresses before and after the stick-slip were divided by the normal stress to obtain the static friction coefficient and the dynamic friction coefficient, respectively [ 18 ]. The curve illustrating the relationship between the loading rate and the static friction coefficient and the curve illustrating the correlation between the loading rate and the dynamic friction coefficient were plotted based on the averages of the static friction coefficients and the dynamic friction coefficients of the first three stick-slips at each loading rate ( Fig 4 ). As can be seen from Fig 4 , as the loading rate increased, the static friction coefficient fluctuated, implying an insignificant correlation between the loading rate and the static friction coefficient. Whereas, the dynamic friction coefficient increased as the loading rate increased. According to the above analysis, the slip characteristics during the inter-slip periods were more susceptible to the friction surface, and compared with the slip characteristics during the inter-slip period, the slip characteristics during the stick-slip period were more affected by the loading rate.

https://doi.org/10.1371/journal.pone.0231464.g004

Characteristics of the displacement evolution of the fault stick-slip at different loading rates

The digital speckle correlation method was used to analyze the speckle image on the surface of the specimen collected by the CCD camera during the loading process, thereby obtaining the evolution of the displacement field of the fault stick-slip, the corresponding relationship between the slip displacement of the fault stick-slip, the loading curve, and the evolution characteristics of the slip rate during the fault stick-slip at different loading rates.

Based on the evolution of the displacement field of the fault stick-slip, the evolution characteristics of the displacement of the fault stick-slip were similar under different loading rates. For a single stick-slip, the displacement generally underwent a uniform evolution phase, a non-uniform evolution phase, and an overall slip phase. Taking the deformation evolution analysis of the specimen at a loading rate of 10 μm/s ( Fig 1 ) as an example, the horizontal displacement contour map of the sliding block obtained using the digital speckle correlation method (the displacement direction was the same as the displacement loading direction) is shown in Fig 5 , in which the displacement contour interval was set to 0.02 mm. The point in time shown in Fig 5A corresponds to the time of Marked Point 1 in Fig 3 . When the shear stress was 5.97 MPa, the displacement contours of the sliding block were sparse, the displacement value gradually decreased from the loading end to the fixed end, and the maximum displacement value was approximately 0.11 mm. The point in time shown in Fig 5B is consistent with that of Marked Point 2 in Fig 3 . When the shear stress was 9.69 MPa, the contours near the loading end were relatively dense and approximately parallel, the displacement value gradually decreased from the loading end to the fixed end, and the maximum displacement value was approximately 0.24 mm, indicating that the fault displacement was in the uniform evolution phase. The point in time shown in Fig 5C corresponds to that of Marked Point 3 in Fig 3 . When the shear stress was 13.62 MPa, the displacement of the sliding block at this moment increased significantly compared with that at the previous moment; the contours became denser, but the contours in different areas had different densities; and the maximum displacement value was approximately 0.71 mm, indicating a non-uniform displacement evolution. The point in time shown in Fig 5D is consistent with that of Marked Point 4 in Fig 3 . When the fault stick-slip had already occurred and the shear stress was 13.19 MPa; the displacement of the sliding block experienced a mutation, but the intensity and distribution characteristics of the contours did not change significantly, and the maximum displacement was approximately 0.74 mm; indicating an overall slip phase.

Displacement fields of the sliding blocks (a) Marked Point 1. (b) Marked Point 2. (c) Marked Point 3. (d) Marked Point 4.

https://doi.org/10.1371/journal.pone.0231464.g005

The slip displacement of the fault stick-slip was calculated as follows: a 5 mm × 5 mm computation window 5 mm above and below the fault slip surface was selected, as shown in Fig 6 . The average displacement of the speckles in the computation window represents the displacement of the central point in the computation window, and the difference between the displacement components in the x-direction of the central point in the two computation windows denotes the slip displacement of the fault stick-slip.

https://doi.org/10.1371/journal.pone.0231464.g006

According to the slip displacement of the fault stick-slips at different loading rates, for the same loading rate, there was a positive relationship between the slip displacement of the fault stick-slip and the stress drop, i.e., the stress drop increased with increasing sliding displacement. However, based on a comparison of the different loading rates, there was no relationship between the slip displacement and the stress drop. The evolution characteristics of the slip displacement of the fault stick-slip were analyzed at a loading rate of 4 μm/s. As can be seen from Fig 7 , the sliding displacement of the rock interface was small during the period of slowly increasing shear stress (about 0–89 s). According to the analysis, this stage involved the compaction of the initial micro-bumps, which were randomly distributed by the sliding interface under normal stress. During the stage of approximately linear growth in shear stress (about 89–249 s), the interface sliding displacement increased non-linearly. According to the analysis, this stage was mainly caused by the non-uniform deformation of the sliding interface caused by the shear stress. During the stick-slip period, the interface sliding displacement suddenly increased, corresponding to a sudden drop in the shear stress. During the stick-slip period, the change in the interface sliding displacement was small, and the corresponding shear stress increase approximately linearly. Among them, the stress drop of the first stick-slip was 1.14 MPa, and the slip displacement was 0.10 mm. The stress drop of the second stick-slip was 1.95 MPa, and the slip displacement was 0.16 mm. The stress drop of the third stick-slip was 2.67 MPa, and the slip displacement was 0.27 mm. The stress drop of the fourth stick-slip was 3.03 MPa, and the slip displacement was 0.28 mm. The stress drop of the fifth stick-slip was 3.24 MPa, and the slip displacement was 0.31 mm. The stress drop of the sixth stick-slip was 3.91 MPa, and the slip displacement was 0.39 mm. For a given specimen, the increase in the stress drop occurred due to the sudden increase in the stick-slip displacement of the fault.

https://doi.org/10.1371/journal.pone.0231464.g007

The evolution of the slip rate of the fault during the stick-slip period indicates that the slip rate of the fault increased initially and then decreased; and as the number of stick-slips increased, the rate curve fluctuated and a significant multi-peak evolution occurred. There was no correlation between the slip rate, the stress curve, and the loading rate. Fig 8 shows the evolution of the slip rate of the fault during the stick-slip period at a loading rate of 4 μm/s. As can be seen from Fig 8 , during the first stick-slip event and the second stick-slip event, the sliding rate increased rapidly in the initial stage of stick-slip, and then, it decreased to a stable state. In the third to sixth stick-slip events, the slip rate increased rapidly in the beginning of the slide, and then, it decreased. After this, the rate increased during the decline, reaching a new peak value of the rate, and then, it fluctuated around a stable state. Table 2 shows the increase in slip rate during the initial sticky slip from the first stick-slip to the sixth stick-slip event.

https://doi.org/10.1371/journal.pone.0231464.g008

https://doi.org/10.1371/journal.pone.0231464.t002

According to the above results of the evolution of the displacement field of the fault under different loading rates, the corresponding relationship between the slip displacement, the loading curve of the fault stick-slip, and the evolution characteristics of the slip rate of the fault during the stick-slip periods, the evolution of the displacement fields of the fault stick-slip was similar for different loading rates, showing three phases: uniform evolution, non-uniform evolution, and overall slip. Under different loading conditions, the slip displacement and the rate of the fault stick-slip were not correlated with the stress drop and loading rate of the loading curve.

Magnitude and stress drop of fault stick-slip at different loading rates

Taking the third stress drop of the specimen at a loading rate of 20 μm/s as an example, the duration of the fault stick-slip acquired by the high-speed camera was 0.001 s, the time of the stress drop acquired by the test machine was 0.31 s, and the total stress drop was 0.60 MPa. Consequently, the actual stress drop corresponding to the specimen was 1.93 × 10 −3 MPa.

According to the above method, the effects of the loading rate on the magnitude and stress drop of the fault stick-slip were studied based on the experimental results obtained for the different loading rates.

Fig 9 shows the relationship between the magnitude and the actual stress drop under different loading rates. As can be seen from Fig 9 , under the same vertical stress, the magnitude corresponding to the different loading rates is correlated with the actual stress drop. As the actual stress drop increased, the magnitude increased, indicating an approximately linear evolution. The magnitude obtained in the experiments ranged from −3.3 to −2.7.

https://doi.org/10.1371/journal.pone.0231464.g009

Fig 10 shows the relationship between the magnitude, the actual stress drop, and the loading rate based on their average values. As the loading rate increased, the magnitude decreased; and as the loading rate increased, the actual stress drop decreased.

https://doi.org/10.1371/journal.pone.0231464.g010

The loading rate is negatively correlated with the magnitude, and the actual stress drop is related to the rate-state dependent frictional constitutive relationship. [ 26 , 27 , 28 ] proposed a rate-state-dependent frictional constitutive relationship after a large number of experimental studies, which explains the friction and sliding instability mechanism of rocks well. The theory holds that friction is a function of the sliding rate and state variables, and the state variables represent the physical state of the contact surface. The sliding fault system has a critical stiffness determined by the friction parameters. When the effective elastic stiffness of the fault is less than the critical stiffness, the system will be unstable, i.e., an earthquake will occur. When the stiffness of the fault is slightly less than or close to the critical stiffness, the instability of the fault gradually becomes insignificant, and this is more characteristic of slow slip. That is, the loading rate and the state variables have an effect on the sliding characteristics of the fault. Based on the evolution results of the effects of the different loading rates on the stick-slip magnitude and stress drop of the fault in this experiment, even if the sliding properties of the fault have not changed, the magnitude and stress drop of the fault also the characteristics of stable sliding.

Conclusions

In this experimental study, we simulated fault stick-slip using a double-sided shear experiment. The stress evolution and displacement evolution characteristics at different loading rates as well as the relationships between the stress drop, magnitude, and loading rate were obtained. The following main conclusions are drawn based on our results.

• The evolutions of the displacement fields of the fault stick-slips were similar for different loading rates, i.e., the displacements exhibited three phases: uniform evolution, non-uniform evolution, and overall slip.
• There was a correlation between the magnitudes corresponding to the different loading rates and the actual stress drop, which was generally exhibited as an approximately linear increase in magnitude with increasing actual stress drop.
• The relationships between the magnitude and the actual stress drop and the loading rate can be generally expressed as follows: the magnitude decreased as the loading rate increased, whereas the actual stress drop decreased as the loading rate increased.
• As the loading rate increased, although the sliding properties of the fault did not change, the magnitude and the stress drop of the fault also exhibited the characteristics of stable sliding.

Acknowledgments

The authors would like to thank Letpub for the English language editing.

• View Article
• Google Scholar
• PubMed/NCBI
• 7. Scuderi M, Collettini C, Viti C, et al. Fabric evolution of quartz-gouge from stable sliding to stick-slip and implications for fault slip mode[C]// Egu General Assembly Conference. EGU General Assembly Conference Abstracts, 2017.

• Access through  your organization
• Purchase PDF

Article preview

Introduction, section snippets, references (52).

Tribology International

Measurement of slip length and friction reduction: an experimental study about boundary slip using omniphobic and 2d coatings.

• • There is an intrinsic link between boundary slip and superlubricity. Theoretically, boundary slip can reduce the velocity gradient of the lubricant, thereby lowering the coefficient of friction (COF) and even achieving superlubricity. However, due to limitations in experimental techniques, the slip length cannot be precisely measured, leaving the mechanism of boundary slip controversial. This paper aims to accurately measure the slip length at the solid-liquid interface under oil-lubricated elastohydrodynamic lubrication (EHL) conditions using experimental methods, and to explore the friction reduction due to boundary slip.
• • Coating methods are employed to induce boundary slip at the solid-liquid interface, and optical interferometry is used to observe the impact of boundary slip on the film thickness. Friction tests are conducted to investigate the effect of boundary slip on the COF. The study reveals that both omniphobic (lotus leaf essence) coatings and two-dimensional (2D) material (MoS2) coatings facilitate boundary slip.
• • Boundary slip on a static surface has little impact on the film thickness, while boundary slip on a moving surface results in a significant reduction in film thickness. Under oil-lubricated EHL conditions, boundary slip at the solid-liquid interface effectively reduces the COF. This study introduces a method for accurately measuring slip length, and using this method, the slip length of the MoS2 coating interface has been measured, revealing that slip lengths vary at different positions in the contact area.
• • Furthermore, as the shear rate increases, the solid-liquid interface transitions from no boundary slip to a linear boundary slip stage, and finally to a nonlinear boundary slip stage influenced by critical shear stress. The slip length measurement method proposed in this study builds a bridge between oil film thickness and slip length, successfully addressing a key issue in boundary slip research. The findings confirm the significant friction reduction due to boundary slip.

Graphical abstract

• Download: Download high-res image (211KB)
• Download: Download full-size image

Selection and characterization of coatings

Experimental equipment and methods, selection of conditions, experimental equipment and method, declaration of interest statement, statement of originality, credit authorship contribution statement, acknowledgement, macroscale superlubricity under extreme pressure enabled by the combination of graphene-oxide nanosheets with ionic liquid, superlubricity of ptfe triggered by green ionic liquids, appl surf sci, macroscale superlubricity of steel by polymer-based ionic liquids without a running-in period, robust and universal macroscale superlubricity with natural phytic acid solutions, enhanced superlubricity on ac films by lubrication with 3-hydroxypropionic acid, smart superamphiphobic surface manipulating wetting behaviors of oil droplet in water, recent progress in superhydrophobic and superamphiphobic coatings for magnesium and its alloys, j magnes alloy, recent advances in superhydrophobic composites based on clay minerals, appl clay sci, synthesis of graphene oxide-based nanofillers and their influence on the anticorrosion performance of epoxy coating in saline medium, diam relat mater, effects of interface wettability on microscale flow by molecular dynamics simulation, int j heat mass transf, lubricant behaviour in concentrated contact systems—the castor oil-steel system, evidence of lubricant slip on steel surface in ehl contact, facilitating effective hydrodynamic lubrication for zero-entrainment-velocity contacts, shear rate and pressure effects on boundary slippage in highly stressed contacts, advances in application and preparation research on molybdenum disulfide, china molybdenum industry, superlubricity, robust microscale structural superlubricity between graphite and nanostructured surface, robust microscale superlubricity under high contact pressure enabled by graphene-coated microsphere, tunable macroscale structural superlubricity in two-layer graphene via strain engineering, macroscale superlubricity enabled by graphene nanoscroll formation, superlubricity of black phosphorus as lubricant additive, acs appl. mater. interfaces.

• Navier C. Mémoire sur les lois du mouvement des fluides. éditeur inconnu;...

Tunable pulsewidth nanosecond laser texturing: From environment friendly superhydrophobic to superamphiphobic surfaces

Graphene–graphene interactions: friction, superlubricity, and exfoliation, friction characteristics of mechanically exfoliated and cvd-grown single-layer mos 2, limits of the hydrodynamic no-slip boundary condition, phys rev lett, cited by (0).