experimental rejection of observer independence in the quantum world

Subscribe to the PwC Newsletter

Join the community, edit social preview.

experimental rejection of observer independence in the quantum world

Add a new code entry for this paper

Remove a code repository from this paper, mark the official implementation from paper authors, add a new evaluation result row.

TASK	DATASET	MODEL	METRIC NAME	METRIC VALUE	GLOBAL RANK	REMOVE

Remove a task

Add a method, remove a method, edit datasets, experimental rejection of observer-independence in the quantum world.

13 Feb 2019 · Massimiliano Proietti , Alexander Pickston , Francesco Graffitti , Peter Barrow , Dmytro Kundys , Cyril Branciard , Martin Ringbauer , Alessandro Fedrizzi · Edit social preview

The scientific method relies on facts, established through repeated measurements and agreed upon universally, independently of who observed them. In quantum mechanics, the objectivity of observations is not so clear, most dramatically exposed in Eugene Wigner's eponymous thought experiment where two observers can experience fundamentally different realities. While observer-independence has long remained inaccessible to empirical investigation, recent no-go-theorems construct an extended Wigner's friend scenario with four entangled observers that allows us to put it to the test. In a state-of-the-art 6-photon experiment, we here realise this extended Wigner's friend scenario, experimentally violating the associated Bell-type inequality by 5 standard deviations. This result lends considerable strength to interpretations of quantum theory already set in an observer-dependent framework and demands for revision of those which are not.

Code Edit Add Remove Mark official

Social Psychology
Rejection (Psychology)

Experimental rejection of observer-independence in the quantum world

February 2019

Heriot-Watt University
This person is not on ResearchGate, or hasn't claimed this research yet.

Discover the world's research

25+ million members
160+ million publication pages
2.3+ billion citations

No file available

To read the file of this research, you can request a copy directly from the authors.

OPT EXPRESS

Alessandro Fedrizzi

Jian-Wei Pan

Anton Zeilinger
Karl Popper
Arthur Fine
David Deutsch
Thomas Herbst

D Frauchiger
PHYS REV LETT
F Graffitti
J Kelly-Massicotte
A M Brańczyk
T Yamashita
J.-Å Larsson
G C Ghirardi
REV MOD PHYS
H I Everett
INT J THEOR PHYS
J Calsamiglia
N Lutkenhaus
S L Braunstein
P H Eberhard
Recruit researchers
Join for free
Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

We're Hiring!
Help Center

Experimental rejection of observer-independence in the quantum world

Related Papers

Eric Cavalcanti

Does quantum theory apply at all scales, including that of observers? A resurgence of interest in the long-standing Wigner's friend paradox has shed new light on this fundamental question. Here---building on a scenario with two separated but entangled "friends" introduced by Brukner---we rigorously prove that if quantum evolution is controllable on the scale of an observer, then one of the following three assumptions must be false: "No-Superdeterminism", "Locality", or "Absoluteness of Observed Events" (i.e. that every observed event exists absolutely, not relatively). We show that although the violation of Bell-type inequalities in such scenarios is not in general sufficient to demonstrate the contradiction between those assumptions, new inequalities can be derived, in a theory-independent manner, which are violated by quantum correlations. We demonstrate this in a proof-of-principle experiment where a photon's path is deemed an obser...

Conference on Lasers and Electro-Optics

The Wigner’s friend paradox illuminates the quantum measurement problem. We derive—and study, in a series of entangled-photon experiments—a new and robust no-go theorem based on the paradox, with stronger constraints than Bell's theorem.

AOS Australian Conference on Optical Fibre Technology (ACOFT) and Australian Conference on Optics, Lasers, and Spectroscopy (ACOLS) 2019

Bahram Borgheai

arXiv (Cornell University)

Foundations of Physics

Tony Sudbery

Journal of Optics B: Quantum and Semiclassical Optics

joseph samuel

Gregg Jaeger

Philosophy of Science

Richard Healey

Physical review letters

Waldimar Amaya

Local realism is the worldview in which physical properties of objects exist independently of measurement and where physical influences cannot travel faster than the speed of light. Bell's theorem states that this worldview is incompatible with the predictions of quantum mechanics, as is expressed in Bell's inequalities. Previous experiments convincingly supported the quantum predictions. Yet, every experiment requires assumptions that provide loopholes for a local realist explanation. Here, we report a Bell test that closes the most significant of these loopholes simultaneously. Using a well-optimized source of entangled photons, rapid setting generation, and highly efficient superconducting detectors, we observe a violation of a Bell inequality with high statistical significance. The purely statistical probability of our results to occur under local realism does not exceed 3.74×10^{-31}, corresponding to an 11.5 standard deviation effect.

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

A quantum experiment suggests there’s no such thing as objective reality

Emerging Technology from the arXiv archive page

Back in 1961, the Nobel Prize–winning physicist Eugene Wigner outlined a thought experiment that demonstrated one of the lesser-known paradoxes of quantum mechanics. The experiment shows how the strange nature of the universe allows two observers—say, Wigner and Wigner’s friend—to experience different realities.

Since then, physicists have used the “Wigner’s Friend” thought experiment to explore the nature of measurement and to argue over whether objective facts can exist. That’s important because scientists carry out experiments to establish objective facts. But if they experience different realities, the argument goes, how can they agree on what these facts might be?

That’s provided some entertaining fodder for after-dinner conversation, but Wigner’s thought experiment has never been more than that—just a thought experiment.

Last year, however, physicists noticed that recent advances in quantum technologies have made it possible to reproduce the Wigner’s Friend test in a real experiment. In other words, it ought to be possible to create different realities and compare them in the lab to find out whether they can be reconciled.

And today, Massimiliano Proietti at Heriot-Watt University in Edinburgh and a few colleagues say they have performed this experiment for the first time: they have created different realities and compared them. Their conclusion is that Wigner was correct—these realities can be made irreconcilable so that it is impossible to agree on objective facts about an experiment.

Wigner’s original thought experiment is straightforward in principle. It begins with a single polarized photon that, when measured, can have either a horizontal polarization or a vertical polarization. But before the measurement, according to the laws of quantum mechanics, the photon exists in both polarization states at the same time—a so-called superposition.

Wigner imagined a friend in a different lab measuring the state of this photon and storing the result, while Wigner observed from afar. Wigner has no information about his friend’s measurement and so is forced to assume that the photon and the measurement of it are in a superposition of all possible outcomes of the experiment.

Wigner can even perform an experiment to determine whether this superposition exists or not. This is a kind of interference experiment showing that the photon and the measurement are indeed in a superposition.

From Wigner’s point of view, this is a “fact”—the superposition exists. And this fact suggests that a measurement cannot have taken place.

But this is in stark contrast to the point of view of the friend, who has indeed measured the photon’s polarization and recorded it. The friend can even call Wigner and say the measurement has been done (provided the outcome is not revealed).

So the two realities are at odds with each other. “This calls into question the objective status of the facts established by the two observers,” say Proietti and co.

That’s the theory, but last year Caslav Brukner, at the University of Vienna in Austria, came up with a way to re-create the Wigner’s Friend experiment in the lab by means of techniques involving the entanglement of many particles at the same time.

The breakthrough that Proietti and co have made is to carry this out. “In a state-of-the-art 6-photon experiment, we realize this extended Wigner’s friend scenario,” they say.

They use these six entangled photons to create two alternate realities—one representing Wigner and one representing Wigner’s friend. Wigner’s friend measures the polarization of a photon and stores the result. Wigner then performs an interference measurement to determine if the measurement and the photon are in a superposition.

The experiment produces an unambiguous result. It turns out that both realities can coexist even though they produce irreconcilable outcomes, just as Wigner predicted.

That raises some fascinating questions that are forcing physicists to reconsider the nature of reality.

The idea that observers can ultimately reconcile their measurements of some kind of fundamental reality is based on several assumptions. The first is that universal facts actually exist and that observers can agree on them.

But there are other assumptions too. One is that observers have the freedom to make whatever observations they want. And another is that the choices one observer makes do not influence the choices other observers make—an assumption that physicists call locality.

If there is an objective reality that everyone can agree on, then these assumptions all hold.

But Proietti and co’s result suggests that objective reality does not exist. In other words, the experiment suggests that one or more of the assumptions—the idea that there is a reality we can agree on, the idea that we have freedom of choice, or the idea of locality—must be wrong.

Of course, there is another way out for those hanging on to the conventional view of reality. This is that there is some other loophole that the experimenters have overlooked. Indeed, physicists have tried to close loopholes in similar experiments for years, although they concede that it may never be possible to close them all.

Nevertheless, the work has important implications for the work of scientists. “The scientific method relies on facts, established through repeated measurements and agreed upon universally, independently of who observed them,” say Proietti and co. And yet in the same paper, they undermine this idea, perhaps fatally.

The next step is to go further: to construct experiments creating increasingly bizarre alternate realities that cannot be reconciled. Where this will take us is anybody’s guess. But Wigner, and his friend, would surely not be surprised.

Ref: arxiv.org/abs/1902.05080 : Experimental Rejection of Observer-Independence in the Quantum World

Keep Reading

Why OpenAI’s new model is such a big deal

The bulk of LLM progress until now has been language-driven. This new model enters the realm of complex reasoning, with implications for physics, coding, and more.

James O'Donnell archive page

A controversial Chinese CRISPR scientist is still hopeful about embryo gene editing. Here’s why.

He Jiankui, who went to prison for three years for making the world’s first gene-edited babies, talked to MIT Technology Review about his new research plans.

Zeyi Yang archive page

Meet the radio-obsessed civilian shaping Ukraine’s drone defense

Since Russia’s invasion, Serhii “Flash” Beskrestnov has become an influential, if sometimes controversial, force—sharing expert advice and intel on the ever-evolving technology that’s taken over the skies. His work may determine the future of Ukraine, and wars far beyond it.

Charlie Metcalfe archive page

A photo illustration depicting gene editing and the US patent language for CRISPR

Two Nobel Prize winners want to cancel their own CRISPR patents in Europe

There’s a surprise twist in the battle to control genome editing.

Antonio Regalado archive page

Stay connected

Get the latest updates from mit technology review.

Discover special offers, top stories, upcoming events, and more.

Thank you for submitting your email!

It looks like something went wrong.

We’re having trouble saving your preferences. Try refreshing this page and updating them one more time. If you continue to get this message, reach out to us at [email protected] with a list of newsletters you’d like to receive.

IEEE Account

Change Username/Password
Update Address

Purchase Details

Payment Options
Order History
View Purchased Documents

Experimental rejection of observer-independence in the quantum world

observer-dependece

Paper Review: Experimental Rejection of Observer-independence in the Quantum World

The MIT Technology Review recently published an article entitled “ A quantum experiment suggests there’s no such thing as objective reality “. This sounds rather spicy: if this were true, and there were no objective reality, what would that mean? Would the postmodernists be right? Would it all be purely subjective? How about claims like “there is no objective reality”–is that an objective fact? If not, how does this all hang together?

Maybe you think this is a case of the media blowing something out of proportion, or getting the science wrong. Surely the title of the original paper is something esoteric and boring like “K-alpha particles exhibit decoherence along mesa-keta spectra at 196mmz intervals” or some other Star Trek made up sounding jargon. But then you look at the title of the paper:

“ Experimental rejection of observer-independence in the quantum world “

Uh-oh. This sounds like a ( rare? ) case where maybe the media are actually reporting accurately on the science—the title would certainly suggest that the scientists believe their experiment rejects objective reality, or something like that. Maybe this is just the scientists selling the paper? So then you read the abstract:

“The scientific method relies on facts, established through repeated measurements and agreed upon universally, independently of who observed them. In quantum mechanics, the objectivity of observations is not so clear, most dramatically exposed in Eugene Wigner’s eponymous thought experiment where two observers can experience fundamentally different realities. While observer-independence has long remained inaccessible to empirical investigation, recent no-go-theorems construct an extended Wigner’s friend scenario with four entangled observers that allows us to put it to the test. In a state-of-the-art 6-photon experiment, we here realise this extended Wigner’s friend scenario, experimentally violating the associated Bell-type inequality by 5 standard deviations. This result lends considerable strength to interpretations of quantum theory already set in an observer-dependent framework and demands for revision of those which are not.”

Hmm. Well. The scientists themselves do in fact seem to be claiming that their experiment gives strong support for an observer-dependent, entirely subjective reality. Even if we wanted to read charitably, and think that this kind of subjectivity was something less exotic and threatening to science, like the kind of observer dependent properties of relativity , we reread the first line of the abstract. The kind of objective facts the authors seem to have in mind are the kind that make science possible. This suggests a much deeper rejection of an objective world than the kind found in relativity (which does not in fact reject an object world, but merely has no privileged reference frame ).

Let us take a closer look at the actual text of the paper, then. Throughout my analysis I will also reference the latest entry of the “ Philosopher’s On ” series of the philosophy site Daily Nous . I’ll link to it a few more times throughout the paper. I’d recommend anyone reading my post, which in some ways takes a bit of a deeper dive into the content of the paper, to read the Daily Nous post after. It is very helpful and enlightening.

When talking about the experiment (which I will discuss in a minute) the scientists write, suggestively, “Can one reconcile their different records, or are they fundamentally incompatible—so that they cannot be considered objective, observer-independent ‘facts of the world’?” (p. 2). They will claim later in the paper that the answer is likely “no”. Indeed, they write in their conclusion:

“Modulo the potential loopholes and accepting the photons’ status as observers, the violation of inequality (2) implies that at least one of the three assumptions of free choice, locality, and observer-independent facts must fail…[one] option is to give up observer independence completely by considering facts only relative to observers…This choice, however, requires us to embrace the possibility that different observers irreconcilably disagree about what happened in an experiment.” (p. 4)

The sections over which I elided describe the other options; options which I will later argue are better. However, it is clear that the conclusion these scientists prefer is to give up an objective, observer independent world. Why is this?

To understand their argument, first we should understand a few things from the previous excerpt: what exactly was the experiment? What are the three conditions–free choice, locality, and observer-independent facts?

The experiment they conducted was a modification of the famous Wigner’s Friend thought experiment.

Wigner asks us to consider a physical system prepared in a superposition. For example, the system might be an electron, and the electron might be in a superposition of being spin-up and spin-down. What exactly is a superposition? I think an example might be helpful: consider the case in which we are interested in the location of an electron. In particular, we want to know if it in a certain room, or outside the room. We can represent the particle and its room-position (which is a binary observable with two possible values: in the room and out of the room ) using the mathematics of quantum mechanics. There is a rule in quantum mechanics called the eigenstate-eigenvalue link (see here for an introduction and history of the rule), that says that the particle has a room-position if and only if the mathematical vector describing the physical system is in an eigenstate of the mathematical object describing room-position observable. This sounds technical, so let’s unpack it a little. Suppose we have a clock:

We can think of the clock as being a Hilbert Space — mathematical object physicists use to describe the state of a physical system. How do we represent whether the particle is in or out of the room? We represent such a property using two vectors at right angles to each other. For example, the two vectors very sketchily drawn here:

The vertical line might represent being in the room, and the horizontal one out of the room. Suppose the state of the particle is represented by the minute hand. The eigenstate-eigenvalue link says that the particle has a position if and only if the minute hand lies on one of the blue lines. In this case, since the minute hand does not lie on one of the blue lines, the particle does not have a position! In this case, we say that the particle is in a superposition of being in the room and out of the room. What is important to note is that even though the particle does not have a definite position, it does have a state–the one represented by the minute hand. In principle, we could design a measuring device to see whether that particle is in that state. This means we can measure whether or not the particle is in a superposition.

Thus, like in the above picture, it can be false that the particle is either in the room or out of the room. Note this is not a contradiction. It is true that the particle is not in the room, and it is not out of the room. However, these are not the only two possibilities. Instead, as I said above, we describe the particle as being in a superposition of being in the room and out of the room. This might be rather shocking, since it seems to defy classical logic. However, it does not. It is rather analogous to a case in which someone believes that every object is either black or white. Thus, for a person with such a conception of colour, the statement “every object is either black or white” seems tautologically true. However, one day this person encounters a red rose. For this person, this might initially feel like a violation of logic. However, upon reflection, she comes to the realization that instead of violating logic, this observation instead demonstrated that she had had an incorrect theory of the possible colours an object might be. The case is the same in quantum mechanics. The electron lacking a position does not defy logic; we rather have to enlarge our initially impoverished space of possible properties.

So, for the Wigner’s Friend thought experiment, we have a particle in a superposition of some property–say, X-spin. Furthermore, suppose we have an observer–Wigner. Since Wigner is a physical system, we can describe him using the mathematics of quantum mechanics. Suppose the friend is to measure the particle, and then Wigner is to measure whether or not his friend and the physical system are in a superposition. Here is how the scientists describe the thought experiment (edited a little to remove some of the math; edits marked with “[*]”):

“According to quantum theory, the friend randomly observes one of the two possible outcomes in every run of the experiment. The friend’s record, [up] or [down], can be stored in one of two possible orthogonal states of some physical memory, labeled either [“electron is up”] or [“electron is down”], and constitutes a “fact” from the friend’s point of view. Wigner observes from outside the isolated laboratory and has no information about his friend’s measurement outcome. According to quantum theory Wigner must describe the friend’s measurement as a unitary interaction that leaves the photon and friend’s record [an] the entangled state… Wigner can now perform an interference experiment in this entangled basis to verify that the photon and his friend’s record are indeed in superposition—a “fact” from his point of view, from which he concludes that his friend cannot have recorded a definite outcome. Concurrently however, the friend does always record a definite outcome, which suggests that the original superposition was destroyed and Wigner should not observe any interference. The friend can even tell Wigner that she recorded a definite outcome (without revealing the result), yet Wigner and his friend’s respective descriptions remain unchanged [6]. This calls into question the objective status of the facts established by the two observers” (pp. 1-2)

This is the tension: from the friend’s perspective, the electron has a determinate X-spin. From Wigner’s, however, the friend and the particle are in a superposition. Thus, the reasoning in this paper goes, there is no objective reality (or at the very least this is called into question).

The actual experiment that the scientists performed is not exactly Wigner’s friend, but what they call an extension of Wigner’s friend. There is another famous type of experiment in quantum mechanics that is meant to confirm the violation of something called a Bell-type inequality . Named after John Bell, he used it to prove his famous theorem , which states that any physical theory that reproduces the probabilistic predictions of quantum mechanics will have to reject a locality condition (to be discussed shortly). There is a vast literature on what exactly Bell’s theorem(s) shows. However, what is important to note here is that this is a well-knows result that has been empirically confirmed many times. What I mean by this is that the kind of probabilistic predictions used in Bell’s theorem have been empirically confirmed to be the optimal predictions we could make (of course things are a little more subtle, but this is the gist–quantum mechanics is the most successful physical theory we have ever written down; as Everett put it, “This formulation describes a wealth of experience. No experimental evidence is known which contradicts it.”).

The experiment discussed in the paper is a combination of Wigner’s friend and the kind of experiment used to test whether Bell’s equality is violated (which is what quantum mechanics predicts). However, the key thing that the experiments were after was whether or not there are “observer-independent fact”–this depends much more on the Wignerian aspect of their experiment than the Bell aspect. (Indeed, it seems to me, and others I will point to later, is that combining these two is a kind of red herring, and is uninteresting.) Karen Crowther on Daily Nous gives a good description of the actual experiment:

“Now, what the experiment actually did was to use QM to calculate the probabilities of each of the possible measurement outcomes, and then compare these to the probabilities calculated from the experimental data obtained (1794 six-photon coincidence events, using 64 settings, over a total of 360 hours). The experimenters did this in order to test the violation of a Bell-type inequality, and the experiment was indeed successful in confirming its violation.”

So, we have a decent understanding now of what the experiment was. Whether or not this experiments actually lends support to what the scientists claim it does, I will leave for later. For now let’s get a handle on the three conditions needed for their theoretical result: free choice, locality, and observer-independent facts.

I’ve actually discussed the free choice condition on this blog before , so I won’t go into too much detail (this will be a long enough post already). The key idea is that the observers of the experiment can freely choose which property of the physical system to measure: there are no conspiracies of physics in which the experiments are bound to measure certain properties so that the results come out just so. Again, for an extended discussion, see the previous post.

The locality condition means that distant measurements (and physical systems in general) cannot affect each other. For example, if I measure the property of a physical system over at Alpha Centauri, it should not instantaneously affect a system you want to measure on Earth. This is somewhat motivated by wanting a quantum mechanics to be consistent with special relativity which imposes a kind of locality constraint, and somewhat motivated by intuition. However, almost every theory of quantum mechanics violates locality; it seems to be something we might have to give up. We’ll discuss this point more a little later.

The final condition is “observer independent facts”. The paper is a little vague and unclear about what this means. Thus from the paper itself it is unclear how this requirement interacts with their result. However, in one of the papers that the experimental paper cites, the condition is specified more clearly. Put plainly, this assumption is that “One can jointly assign truth values to the propositions about observed outcomes (“facts”) of different observers” (p. 5 from the paper linked immediately above). The paper also gives a slightly more technical account of this postulate, but this is sufficient for our purposes here.

Now we have a handle on the experiment, and the three conditions needed for the “no-go theorem for observer-independent facts” which the experiments are trying to empirically support. What is their argument, and is it successful?

Recall from the earlier quote from the conclusion of the paper. The theorem says that accepting the conditions of free choice, locality, and observer independent facts is incompatible with their experiments results, since they violate the Bell-type inequality. This much is true. Thus, we must give up one. Which one? They argue for giving up observer-independent facts. However their argument is rather sparse; they briefly mention that “one way to accommodate our result is by proclaiming that ‘facts of the world’ can only be established by a privileged observer—e.g., one that would have access to the ‘global wavefunction’ in the many worlds interpretation or Bohmian mechanics” (p. 4). First of all, this isn’t true–neither Bohmian mechanics nor many worlds needs a privileged observer. Indeed, as Dustin Lazarovici points out the physicist John Bell of the Bell inequality called both Bohmian mechanics and many worlds “quantum theories without an observer.”

After this remark the scientists immediately shift to the thesis of their paper: that we should give up an observer independent reality. However, as we saw, there is no need to do this–we already have theories that account for this! As Wayne Myrvold remarks :

“Here’s a nice fact about claims of this sort: when you see one, you can be sure, without even going through the details of the argument, that any conclusion to the effect that the predictions of quantum mechanics are incompatible with an objective, observer-independent reality, is simply and plainly false. That is because we have a theory that yields all of the predictions of standard quantum mechanics and coherently describes a single, observer-independent world. This is the theory that was presented already in 1927 by Louis de Broglie, and was rediscovered in 1952 by David Bohm, and is either called the de Broglie-Bohm pilot wave theory, or Bohmian mechanics, depending on who you’re talking to. You can be confident that, if you went through the details of any real or imagined experiment, then you would find that the de Broglie-Bohm theory gives a consistent, observer-independent, one-world account of what happens in the experiment, an account that is in complete accord with standard quantum mechanics with regards to predictions of experimental outcomes.

There are other theories, known as dynamical collapse theories, that also yield accounts of a single, observer-independent reality. These theories yield virtually the same predictions as standard quantum mechanics for all experiments that are currently feasible, but differ from the predictions of quantum mechanics for some experiments involving macroscopic objects.”

He doesn’t mention Everttian (many worlds) quantum mechanics in this passage, but it too is compatible with this result. As Sean Carroll in the same Daily Nous piece puts it:

“My own preferred version of quantum mechanics is the Everett, or Many-Worlds formulation. It is a thoroughly realist theory, and is completely compatible with the experimental results obtained here. Thus, we have a proof by construction that this result cannot possibly imply that there is no objective reality.”

What we have to do in order to keep observer-independent facts is to give up a strong form of locality. Pretty much all of our theories of quantum mechanics give up locality. But we already knew this! It is old news. (Subtle side note: even though Everettian quantum mechanics and GRW flashes are non-local in the sense needed to give the standard quantum mechanical predictions, they are still (very likely) compatible with special relativity. This is not essential for our story here, but is worth mentioning.) Indeed, as Tim Maudlin remarks (you already know whence this quote comes!):

“All of this is even spelled out in the article itself: ‘But there are other assumptions too. One is that observers have the freedom to make whatever observations they want. And another is that the choices one observer makes do not influence the choices other observers make—an assumption that physicists call locality.’ That is, in order to account for the outcome of this experiment, one has to deny that physical reality is local in Bell’s sense. (This gloss on the locality condition is not accurate, but leave that aside.) That is something we have known for 50 years.”

Thus we see that the experimental results really show nothing new, and certainly nothing that should make us question objective reality. It really does seem to be an unfortunate case of physicists either being confused, or trying to sell their result too much (inclusive or!). The most charitable reading of these results I could find is by Karen Crowther whom I referenced earlier:

“The question is what this experiment demonstrates about QM that was not already known from the thought-experiment plus previous experimental results. Plausibly, what it shows is that a scenario analogous to the one imagined by Wigner is in fact physically possible, and in it the observers do record conflicting facts.”

The least charitable (but also very amusing) quote I encountered was from Dustin Lazarovici:

“In my opinion, the paper does indeed raise some important questions, though they are mostly sociological ones. For instance: Why does physics tend to get exposure and attention merely for making outlandish claims, regardless of their scientific substance? And why do even many experts tend to abandon rational and critical standards when it comes to quantum mechanics? Why, in other words, have we gotten so used to quantum physics being crazy that even the most outlandish claims come with a presupposition of plausibility and relevance?

As a matter of fact, quantum mechanics can be as clear and rational as any respectable theory that came before it. You just have to do it right.”

I have to agree with this sentiment. Although, as for his first question, I think we can explain that by noticing that humans tend to be more interested in outlandish claims like “THERE IS NO OBJECTIVE REALITY”. Again, no one wants to read the paper entitled “K-alpha particles exhibit decoherence along mesa-keta spectra at 196mmz intervals”. It’s not sexy enough to rise to the surface of the MIT Technology Review.

I think the message to take away from all of this is that objective reality is fine, and nothing has really changed at all in quantum mechanics because of this result. I’ll give the last words to Wayne Myrvold:

“Headline news! Stop the presses! A group of experimenters did an experiment, and the results came out exactly the way that our best physical theory of such things says it should, just as everyone expected. Quantum Theory Confirmed Again .

That’s what actually happened, though you’d never know it from the clickbait headline: A quantum experiment suggests there’s no such thing as objective reality .”

Experimental test of local observer-independence

The scientific method relies on facts, established through repeated measurements and agreed upon universally, independently of who observed them. In quantum mechanics, the objectivity of observations is not so clear, most dramatically exposed in Eugene Wigner’s eponymous thought experiment where two observers can experience seemingly different realities. The question whether these realities can be reconciled in an observer-independent way has long remained inaccessible to empirical investigation, until recent no-go-theorems constructed an extended Wigner’s friend scenario with four observers that allows us to put it to the test. In a state-of-the-art 6-photon experiment, we realise this extended Wigner’s friend scenario, experimentally violating the associated Bell-type inequality by 5 standard deviations. If one holds fast to the assumptions of locality and free-choice, this result implies that quantum theory should be interpreted in an observer-dependent way.

Introduction.—

The observer’s role as final arbiter of universal facts Popper ( 1992 ) was imperilled by the advent of 20 th th {}^{\textrm{th}} century science. In relativity, previously absolute observations are now relative to moving reference frames; in quantum theory, all physical processes are continuous and deterministic, except for observations, which are proclaimed to be instantaneous and probabilistic. This fundamental conflict in quantum theory is known as the measurement problem, and it originates because the theory does not provide a clear cut between a process being a measurement or just another unitary physical interaction.

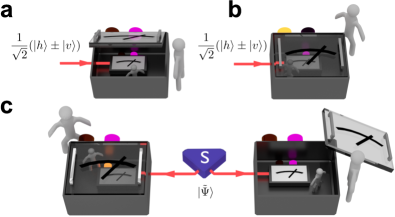
This is best illustrated in the seminal “Wigner’s friend” thought experiment Wigner ( 1961 ) , whose far-reaching implications are only starting to become clear Brukner ( 2015 , 2018 ); Frauchiger and Renner ( 2018 ) . Consider a single photon in a superposition of horizontal | h ⟩ ket ℎ |h\rangle and vertical polarisation | v ⟩ ket 𝑣 |v\rangle , measured in the { | h ⟩ , | v ⟩ } ket ℎ ket 𝑣 \{|h\rangle,|v\rangle\} -basis by an observer—Wigner’s friend—in an isolated lab, see Figs. 1 a and b . According to quantum theory, the friend randomly observes one of the two possible outcomes in every run of the experiment. The friend’s record, h ℎ h or v 𝑣 v , can be stored in one of two possible orthogonal states of some physical memory, labeled either | “photon is h ” ⟩ ket “photon is h ” |\text{``photon is {h}''}\rangle or | “photon is v ” ⟩ ket “photon is v ” |\text{``photon is {v}''}\rangle , and constitutes a “fact” from the friend’s point of view. Wigner, who observes the isolated laboratory from the outside, has no information about his friend’s measurement outcome. According to quantum theory Wigner must describe the friend’s measurement as a unitary interaction that leaves the photon and friend’s record in the entangled state (with implicit tensor products):



			(1)

Wigner can now perform an interference experiment in an entangled basis containing the states of Eq. ( 1 ) to verify that the photon and his friend’s record are indeed in a superposition—a “fact” from his point of view. From this fact, Wigner concludes that his friend cannot have recorded a definite outcome. Concurrently however, the friend does always record a definite outcome, which suggests that the original superposition was destroyed and Wigner should not observe any interference. The friend can even tell Wigner that she recorded a definite outcome (without revealing the result), yet Wigner and his friend’s respective descriptions remain unchanged Deutsch ( 1985 ) . This calls into question the objective status of the facts established by the two observers. Can one reconcile their different records, or are they fundamentally incompatible—so that they cannot be considered objective, observer-independent “facts of the world” Brukner ( 2015 , 2018 ) ?

(2)

As shown in Refs. Brukner ( 2015 , 2018 ) , a violation of the inequality above is, however, possible in a physical world described by quantum theory. Such a violation would demonstrate that the observed probability distributions P ( A x , B y ) 𝑃 subscript 𝐴 𝑥 subscript 𝐵 𝑦 P(A_{x},B_{y}) are incompatible with assumptions F, L, and O. Therefore, if we accept F and L, it follows that the pieces of information corresponding to facts established by Alice, Bob, and their friends cannot coexist within a single, observer-independent framework Brukner ( 2015 , 2018 ) . Notably this is the case even though Alice and Bob can acknowledge the occurrence of a definite outcome in their friend’s closed laboratory.

We note that, although Bell’s mathematical machinery Bell and Aspect ( 2004 ) is used to show the result, the set of assumptions considered here—and therefore the conclusions that can be drawn from a violation of inequality ( 2 )—are different from those in standard Bell tests. In fact, while they share assumptions L and F, the third assumption of predetermination (PD) in the original Bell theorem Bell ( 1964 ) , for instance, differs from our assumption O in that it is only concerned with the deterministic (or otherwise) nature of measurement outcomes, not with their objectivity as in O. A Bell test is indifferent to the observables used and the underlying system, such that any violation suffices to rule out the conjunction of L, F and PD. In contrast, a Bell-Wigner test is based on very specific observables that satisfy the definition of an observation given below and thus represent facts relative to different observers. Formally, any Bell-Wigner violation implies a Bell-violation, but not the other way round.

Before we describe our experiment in which we test and indeed violate inequality ( 2 ), let us first clarify our notion of an observer. Formally, an observation is the act of extracting and storing information about an observed system. Accordingly, we define an observer as any physical system that can extract information from another system by means of some interaction, and store that information in a physical memory.

Such an observer can establish “facts”, to which we assign the value recorded in their memory. Notably, the formalism of quantum mechanics does not make a distinction between large (even conscious) and small physical systems, which is sometimes referred to as universality. Hence, our definition covers human observers, as well as more commonly used non-conscious observers such as (classical or quantum) computers and other measurement devices—even the simplest possible ones, as long as they satisfy the above requirements. We note that the no-go theorem formulated in Frauchiger and Renner ( 2018 ) requires observers to be “agents”, who “use” quantum theory to make predictions based on the measurement outcomes. In contrast, for the no-go theorem we tested here Brukner ( 2018 ) it is sufficient that they perform a measurement and record the outcome. The enhanced capabilities required of agents were recently discussed in Baumann and Brukner ( 2019 ) .

0.02 0.10 \mathcal{C}=99.38^{+0.02}_{-0.10}\% , see Supplementary Materials for details. The photon pair from source S 0 subscript 𝑆 0 S_{0} is rotated to

(3)

To test inequality ( 2 ), Alice and Bob then measure the following observables on their respective joint photon / friend’s record systems:




				(4)

(with | Φ photon/record ± ⟩ ket subscript superscript Φ plus-or-minus photon/record |\Phi^{\pm}_{\text{photon/record}}\rangle as defined in Eq. ( 1 )). The observables A 0 subscript 𝐴 0 A_{0} and B 0 subscript 𝐵 0 B_{0} directly unveil the records established by Alice’s and Bob’s friend, respectively. The observables A 1 subscript 𝐴 1 A_{1} and B 1 subscript 𝐵 1 B_{1} , on the other hand, correspond to Alice’s and Bob’s joint measurements on their friend’s photon and record, and define their own facts in the same way as Wigner in the original thought experiment confirms his entangled state assignment.

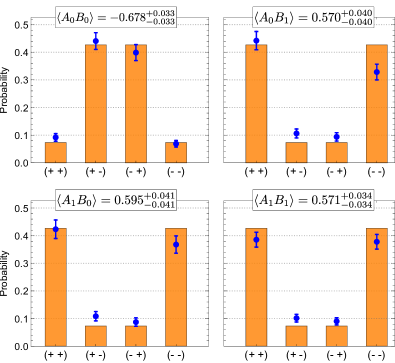
0.075 0.075 S_{\textrm{exp}}=2.416^{+0.075}_{-0.075} , thus violating inequality ( 2 ) by more than 5 5 5 standard deviations. This value is primarily limited by the higher-order photon emissions from our probabilistic photon sources. Statistical uncertainties are independently estimated using an error propagation approach and a Monte-Carlo method. Details are discussed in the Supplementary Materials.

Discussion.—

One might further be tempted to deny our photonic memories the status of “observer”. This, however, would require a convincing revision of our minimal definition of what qualifies as an observer, which typically comes at the cost of introducing new physics that is not described by standard quantum theory. Eugene Wigner, for example, argued that the disagreement with his hypothetical friend could not arise due to a supposed impossibility for conscious observers to be in a superposition state Wigner ( 1961 ) . However, the lack of objectivity revealed by a Bell-Wigner test does not arise in anyone’s consciousness, but between the recorded facts. Since quantum theory does not distinguish between information recorded in a microscopic system (such as our photonic memory) and in a macroscopic system the conclusions are the same for both: the measurement records are in conflict regardless of the size or complexity of the observer that records them. Implementing the experiment with more complex observers would not necessarily lead to new insights into the specific issue of observer-independence in quantum theory. It would however serve to show that quantum mechanics still holds at larger scales, ruling out alternative (collapse) models Ghirardi et al. ( 1986 ) . However, this is not the point of a Bell-Wigner test—less demanding experiments could show that.

Modulo the potential loopholes and accepting the photons’ status as observers, the violation of inequality ( 2 ) implies that at least one of the three assumptions of free choice, locality, and observer-independent facts must fail. The related no-go theorem by Frauchiger & Renner Frauchiger and Renner ( 2018 ) rests on different assumptions which do not explicitly include locality. While the precise interpretation of Ref. Frauchiger and Renner ( 2018 ) within non-local theories is under debate Lazarovici and Hubert ( 2019 ) , it seems that abandoning free choice and locality might not resolve the contradiction Frauchiger and Renner ( 2018 ) . A compelling way to accommodate our result is then to proclaim that “facts of the world” can only be established by a privileged observer—e.g., one that would have access to the “global wavefunction” in the many worlds interpretation Everett ( 1957 ) or Bohmian mechanics Bohm ( 1952 ) . Another option is to give up observer independence completely by considering facts only relative to observers Rovelli ( 1996 ) , or by adopting an interpretation such as QBism, where quantum mechanics is just a tool that captures an agent’s subjective prediction of future measurement outcomes Fuchs ( 2017 ) . This choice, however, requires us to embrace the possibility that different observers irreconcilably disagree about what happened in an experiment. A further interesting question is whether the conclusions drawn from Bell-, or Bell-Wigner tests change under relativistic conditions with non-inertial observers Durham ( 2019 ) .

Popper (1992) K. Popper, Realism and the Aim of Science (Routledge, 1992).
Wigner (1961) E. Wigner, in The Scientist Speculates , edited by I. Good (1961), pp. 284–302.
Brukner (2015) Č. Brukner, arXiv:1507.05255 (2015).
Brukner (2018) Č. Brukner, Entropy 20 , 350 (2018).
Frauchiger and Renner (2018) D. Frauchiger and R. Renner, Nature communications 9 , 3711 (2018).
Deutsch (1985) D. Deutsch, Int. J. Theor. Phys. 24 , 1 (1985).
Healey (2018) R. Healey, Found. Phys. 48 , 1568 (2018).
Baumann et al. (2019) V. Baumann, F. Del Santo, and Č. Brukner, Found. Phys. 49 , 741 (2019).
Fine (1982) A. Fine, Phys. Rev. Lett. 48 , 291 (1982).
Clauser et al. (1969) J. Clauser, M. Horne, A. Shimony, and R. Holt, Phys. Rev. Lett. 23 , 880 (1969).
Bell and Aspect (2004) J. S. Bell and A. Aspect, Speakable and Unspeakable in Quantum Mechanics: Collected Papers on Quantum Philosophy (Cambridge University Press, 2004), 2nd ed.
Bell (1964) J. S. Bell, Physics 1 , 195 (1964).
Baumann and Brukner (2019) V. Baumann and Č. Brukner, arXiv:1901.11274 (2019).
Graffitti et al. (2018a) F. Graffitti, P. Barrow, M. Proietti, D. Kundys, and A. Fedrizzi, Optica 5 , 514 (2018a).
Graffitti et al. (2018b) F. Graffitti, J. Kelly-Massicotte, A. Fedrizzi, and A. M. Brańczyk, Phys. Rev. A 98 , 053811 (2018b).
Jin et al. (2014) R.-B. Jin, R. Shimizu, K. Wakui, M. Fujiwara, T. Yamashita, S. Miki, H. Terai, Z. Wang, and M. Sasaki, Opt. Express 22 , 11498 (2014).
Browne and Rudolph (2005) D. E. Browne and T. Rudolph, Phys. Rev. Lett. 95 , 010501 (2005).
Pan et al. (2001) J.-W. Pan, M. Daniell, S. Gasparoni, G. Weihs, and A. Zeilinger, Phys. Rev. Lett. 86 , 4435 (2001).
Larsson (2014) J.-Å. Larsson, J. Phys. A 47 , 424003 (2014).
Ghirardi et al. (1986) G. C. Ghirardi, A. Rimini, and T. Weber, Phys. Rev. D 34 , 470 (1986).
Lazarovici and Hubert (2019) D. Lazarovici and M. Hubert, Sci. Rep. 9 , 470 (2019).
Everett (1957) H. I. Everett, Rev. Mod. Phys. 29 , 454 (1957).
Bohm (1952) D. Bohm, Phys. Rev. 85 , 166 (1952).
Rovelli (1996) C. Rovelli, Int. J. Theor. Phys. 35 , 1637 (1996).
Fuchs (2017) C. A. Fuchs, Mind and Matter 15 , 245 (2017).
Durham (2019) I. T. Durham, arXiv:1902.09028 (2019).
Fedrizzi et al. (2007) A. Fedrizzi, T. Herbst, A. Poppe, T. Jennewein, and A. Zeilinger, Opt. Express 15 , 15377 (2007).
Broome et al. (2011) M. A. Broome, M. P. Almeida, A. Fedrizzi, and A. G. White, Opt. Express 19 , 22698 (2011).
Calsamiglia and Lutkenhaus (2001) J. Calsamiglia and N. Lutkenhaus, Appl. Phys. B 72 , 67 (2001).
Braunstein and Mann (1995) S. L. Braunstein and A. Mann, Phys. Rev. A 51 , R1727 (1995).
Eberhard (1993) P. H. Eberhard, Phys. Rev. A 47 , 747 (1993).

Acknowledgements We thank Č. Brukner, R. Renner and F. Shahandeh for useful discussions. This work was supported by the UK Engineering and Physical Sciences Research Council (grant number EP/N002962/1, EP/L015110/1) and the French National Research Agency (grant number ANR-13-PDOC-0026). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 801110 and the Austrian Federal Ministry of Education, Science and Research (BMBWF).

Correspondence Correspondence and requests for materials should be addressed to AF (email: [email protected]).

Supplementary materials

Setup details.—.

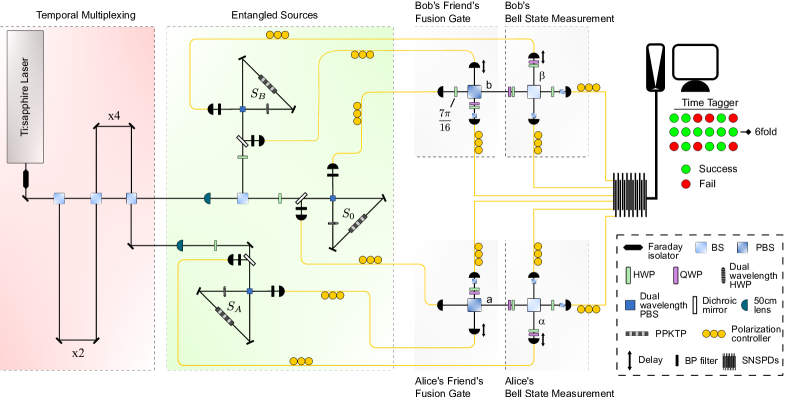
Measurement protocol.—

We now describe in detail the measurement procedure sketched in Fig. 2 . Source S 0 subscript 𝑆 0 S_{0} and the HWP on its right output arm produce an entangled pair of photons in the state of Eq. ( 3 ). This photon pair is distributed to the laboratories of Alice’s friend and Bob’s friend, who measure their photon using Type-I fusion gates Browne and Rudolph ( 2005 ) . Each fusion gate is implemented with a PBS, where horizontally and vertically polarised photons are transmitted and reflected, respectively (by convention collecting a phase i 𝑖 i for the latter). Two photons entering the PBS from two different inputs with opposite polarisation, | h ⟩ | v ⟩ ket ℎ ket 𝑣 |h\rangle|v\rangle or | v ⟩ | h ⟩ ket 𝑣 ket ℎ |v\rangle|h\rangle , will exit from the same output port, and will therefore not lead to coincident detection. Only the coincident | h ⟩ | h ⟩ ket ℎ ket ℎ |h\rangle|h\rangle and | v ⟩ | v ⟩ ket 𝑣 ket 𝑣 |v\rangle|v\rangle components will be recorded in post-selection. For these post-selected photons, the fusion gate induces the following transformations:


				(S1)

where Q/HWP refers to the combination of a quarter-wave plate at π / 4 𝜋 4 \pi/4 and a half-wave plate at π / 8 𝜋 8 \pi/8 behind the PBS (see Fig. 2 ). The second (heralding) photon in the above equation is then projected onto the state | h ⟩ ket ℎ |h\rangle via another PBS. The Type-I fusion gate thus implements the operation

(S2)

where the factor 1 2 1 2 \frac{1}{\sqrt{2}} indicates the success probability of the gate of 1 2 1 2 \frac{1}{2} .

To use the fusion gate to measure photon a 𝑎 a (see Fig. 2 ) non-destructively, Alice’s friend uses an ancilla from the entangled pair created by S A subscript 𝑆 𝐴 S_{A} , prepared as | Ψ − ⟩ α ′ α subscript ket superscript Ψ superscript 𝛼 ′ 𝛼 |\Psi^{-}\rangle_{\alpha^{\prime}\alpha} . Depending on the state of the incoming photon, the operation performed by Alice’s friend transforms the overall state as




				(S3)

Hence, the state | h ⟩ a subscript ket ℎ 𝑎 |h\rangle_{a} or | v ⟩ a subscript ket 𝑣 𝑎 |v\rangle_{a} of the external photon in mode a 𝑎 a is copied, after being flipped ( h ↔ v ↔ ℎ 𝑣 h\leftrightarrow v ), onto Alice’s friend’s photon in mode α 𝛼 \alpha . In other words, this corresponds to a measurement of the incoming photon in the { h , v } ℎ 𝑣 \{h,v\} -basis, with the outcome being recorded in the state of photon α 𝛼 \alpha , such that we can write


			(S4)

The amplitudes 1 2 1 2 \frac{1}{2} in Eq. ( S3 ) indicate the total success probability of 1 4 1 4 \frac{1}{4} for this procedure.

Consider now the central source S 0 subscript 𝑆 0 S_{0} together with Alice’s and Bob’s friends’ laboratories. According to Eq. ( 3 ), the state generated by S 0 subscript 𝑆 0 S_{0} is, after the unitary U 7 π 16 subscript 𝑈 7 𝜋 16 U_{\frac{7\pi}{16}} ,


				(S5)

The transformations induced by Alice’s and Bob’s friends are then, according to Eq. ( S3 ):

(S6)

with a global success probability of 1 16 1 16 \frac{1}{16} . The state


				(S7)

is the four-photon state shared by Alice and Bob when both fusion gates are successful.

Recalling from Eq. ( S4 ) how the friends’ measurement results are encoded in their polarisation states, the observables of Eq. ( 4 ) to be measured on | Ψ ~ ′ ⟩ a α b β subscript ket superscript ~ Ψ ′ 𝑎 𝛼 𝑏 𝛽 |\tilde{\Psi}^{\prime}\rangle_{a\alpha b\beta} are

(S8)

1 1 2 0.427 \frac{1}{4}(1+\frac{1}{\sqrt{2}})\simeq 0.427 , 1 4 ( 1 − 1 2 ) ≃ 0.073 similar-to-or-equals 1 4 1 1 2 0.073 \frac{1}{4}(1-\frac{1}{\sqrt{2}})\simeq 0.073 , or 0 0 . In addition to this result, an alternative measurement protocol for A 0 subscript 𝐴 0 A_{0} and B 0 subscript 𝐵 0 B_{0} is presented below.

Error analysis.—

As described previously, each average value ⟨ A x B y ⟩ delimited-⟨⟩ subscript 𝐴 𝑥 subscript 𝐵 𝑦 \langle A_{x}B_{y}\rangle is calculated from 16 measured 6-fold coincidence counts n i subscript 𝑛 𝑖 n_{i} . These numbers follow a Poisson distribution with variance σ n i 2 = n i superscript subscript 𝜎 subscript 𝑛 𝑖 2 subscript 𝑛 𝑖 \sigma_{n_{i}}^{2}=n_{i} . The uncertainty on ⟨ A x B y ⟩ = f ( n 1 , … , n 16 ) delimited-⟨⟩ subscript 𝐴 𝑥 subscript 𝐵 𝑦 𝑓 subscript 𝑛 1 … subscript 𝑛 16 \langle A_{x}B_{y}\rangle=f(n_{1},\ldots,n_{16}) can then be computed using

(S9)

Since the four averages ⟨ A 1 B 1 ⟩ delimited-⟨⟩ subscript 𝐴 1 subscript 𝐵 1 \langle A_{1}B_{1}\rangle , ⟨ A 1 B 0 ⟩ delimited-⟨⟩ subscript 𝐴 1 subscript 𝐵 0 \langle A_{1}B_{0}\rangle , ⟨ A 0 B 1 ⟩ delimited-⟨⟩ subscript 𝐴 0 subscript 𝐵 1 \langle A_{0}B_{1}\rangle and ⟨ A 0 B 0 ⟩ delimited-⟨⟩ subscript 𝐴 0 subscript 𝐵 0 \langle A_{0}B_{0}\rangle are statistically independent, the uncertainties can be calculated independently and combined to estimate the uncertainty on S 𝑆 S . To take into account potentially asymmetric errors in the limit of small count rates, we computed the uncertainty on the Bell-Wigner parameter S 𝑆 S using a Monte-Carlo routine with 100 000 samples. The values obtained through these two methods agree to within 0.0032 0.0032 0.0032 .

Note that in the results shown in Fig. S3 with the observables of Eq. ( S10 ), errors are correlated due to normalisation with a common total. Accounting for this in the error propagation results in slightly larger statistical uncertainty.

The Bell-Wigner value S e x p subscript 𝑆 𝑒 𝑥 𝑝 S_{exp} that can be achieved experimentally is primarily limited by multi-pair emissions from our probabilistic photon-pair sources. We first note that any emission of 3 pairs from any subset of our 3 sources occurs with roughly similar probability. To exclude unwanted terms we use six-fold coincidence detection, which can only be successful for an emission of one pair each in S 0 subscript 𝑆 0 S_{0} , S A subscript 𝑆 𝐴 S_{A} and S B subscript 𝑆 𝐵 S_{B} , or three pairs in S 0 subscript 𝑆 0 S_{0} . The latter would amount to noise but is excluded by our cross-polarisation design and can thus not lead to a coincidence detection. This leaves higher-order contributions where at least 4 photon pairs are produced as the main source of errors. Since such events scale with a higher exponent of the pump power, they are suppressed in our experiment by working with a relatively low pump power of 100 mW.

Towards a loophole-free “Bell-Wigner” test.—

Since our experiment relies on some of the same assumptions as traditional Bell tests, it is subject to the same conceptual and technical loopholes: locality, freedom of choice, and the detection loophole. Due to the increased complexity of our experiment, compared to a standard Bell test, the practical requirements for closing these loopholes are significantly more challenging. We now briefly discuss how these loopholes could be closed in the future.

The configuration of our experiment makes it analogous to an “event-ready” Bell test, where the detection of the ancilla photons in the fusion gates heralds which events should be kept for the Bell-Wigner test. In such a configuration, closing the locality and freedom of choice loopholes requires the heralding events to be space-like separated from Alice’s and Bob’s setting choices, which should each be space-like separated from the measurement outcome of the other party. This imposes stringent space-time location requirements for a Bell-Wigner test closing these loopholes.

The detection loophole arises because only a fraction of all created photons is detected. In our “event-ready” configuration, the limited success probability of the fusion gates is not an issue: only heralded events will contribute to the Bell-Wigner test. Nevertheless, to ensure that the fusion gates are indeed event-ready, the ancilla detectors should be photon-number-resolving.

ket superscript Ψ |\Psi^{+}\rangle,|\Psi^{-}\rangle , and have a third outcome for | Φ ± ⟩ ket superscript Φ plus-or-minus |\Phi^{\pm}\rangle (see Eq. ( S8 )). This can be realised with a small modification to our setup, with detectors added on the second outputs of Alice’s and Bob’s PBS Braunstein and Mann ( 1995 ) . An even simpler measurement would discriminate e.g. | Ψ − ⟩ ket superscript Ψ |\Psi^{-}\rangle from the other three Bell states, thus measuring the observables A 1 = B 1 = 𝟙 − 2 | Ψ − ⟩ ⟨ Ψ − | subscript 𝐴 1 subscript 𝐵 1 1 2 ket superscript Ψ bra superscript Ψ A_{1}=B_{1}=\mathds{1}-2|\Psi^{-}\rangle\!\langle\Psi^{-}| ; this would not change anything in an ideal implementation, but simplifies the analysis with detection inefficiencies below.

superscript 𝜂 4 1 2 superscript 1 superscript 𝜂 2 2 \langle A_{1}B_{1}\rangle=\eta^{4}\frac{1}{\sqrt{2}}+(1-\eta^{2})^{2} . With these values, the minimal required detection efficiency to violate inequality ( 2 ) with (unrealistically) perfect quantum states and measurements is η > 2 3 ( 1 − 1 2 ) − 1 ≃ 0.875 𝜂 2 3 1 1 2 1 similar-to-or-equals 0.875 \eta>2\sqrt{3(1-\frac{1}{\sqrt{2}})}-1\simeq 0.875 . This is a more stringent requirement than for a standard test of the CHSH inequality, for which a similar analysis for maximally entangled states yields η > 2 2 − 2 ≃ 0.828 𝜂 2 2 2 similar-to-or-equals 0.828 \eta>2\sqrt{2}-2\simeq 0.828 . To relax this requirement, one might attempt similar tricks as for standard Bell tests, e.g. to use non-maximally entangled states Eberhard ( 1993 ) , although this will come at the cost of a reduced violation of the inequality.

Note, finally, that in the conclusions we draw from the violation of inequality ( 2 ), we need to trust that A 0 subscript 𝐴 0 A_{0} and B 0 subscript 𝐵 0 B_{0} indeed directly measure the memory of Alice’s and Bob’s friends, so as to unveil their respective facts. A new loophole may be opened, now specific to Bell-Wigner tests, if such an interpretation cannot be maintained. To address this loophole with a setup like ours, one should use measurement devices for A 0 subscript 𝐴 0 A_{0} and B 0 subscript 𝐵 0 B_{0} that clearly separate the initial systems and the memories of each friend, and only “looks” at the memory photons, rather than at the system photon + memory photon together; we also leave this possibility as a challenge for future Bell-Wigner experimental tests.

Alternative observables A 0 , B 0 subscript 𝐴 0 subscript 𝐵 0 A_{0},B_{0} .—


				(S10)

which have a slightly different physical interpretation. The observables used in the main text and defined in Eq. ( 4 ), directly measure the facts established by the friend, as recorded in their memory. In contrast, the observables in Eq. ( S10 ) can be understood as not only a measurement of the friend’s record (to establish a “fact for the friend”), but also of the original photon measured by the friend, as a consistency check: if the state of the photon is found to be inconsistent with the friend’s record, the definition above assigns a value 0 0 for the measurement result.

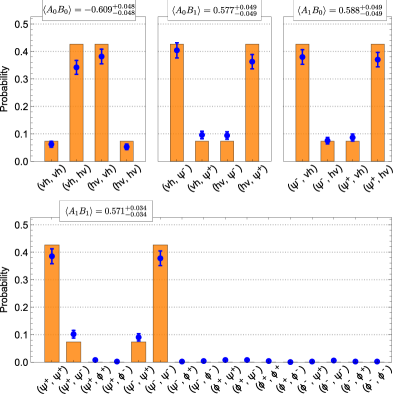
0.073 0.073 S_{exp}=2.407^{+0.073}_{-0.073} , again violating inequality ( 2 ) by more than 5 standard deviations. As in the main text, errors are computed assuming Poissonian photon counting statistics, see below for details.

Alternative measurement protocol for A 0 , B 0 subscript 𝐴 0 subscript 𝐵 0 A_{0},B_{0} .—

Recall that in order to measure A 0 subscript 𝐴 0 A_{0} (similarly B 0 subscript 𝐵 0 B_{0} ), the beam splitter for Alice in Fig. 2 has to be removed relative to the measurement of A 1 subscript 𝐴 1 A_{1} . A less invasive method (which does not compromise the alignment of our optical elements) is to introduce linear polarisers in modes a ( b ) 𝑎 𝑏 a(b) and α ( β ) 𝛼 𝛽 \alpha(\beta) . This effectively measures the photons before the BS, preventing interference.

0.110 0.110 S_{exp}=2.346^{+0.110}_{-0.110} , violating the Bell-Wigner inequality by more than 3 standard deviations. We note that the violation observed with this method is somewhat reduced because of ∼ 4.83 ± 0.97 % similar-to absent plus-or-minus 4.83 percent 0.97 \sim 4.83\pm 0.97\% loss that is introduced by the polarisers. This effectively reduces the number of counts that are observed in the settings A 0 subscript 𝐴 0 A_{0} and B 0 subscript 𝐵 0 B_{0} compared to the normalisation used, and thereby reduces the expectation values ⟨ A 0 B 1 ⟩ delimited-⟨⟩ subscript 𝐴 0 subscript 𝐵 1 \langle A_{0}B_{1}\rangle and ⟨ A 1 B 0 ⟩ delimited-⟨⟩ subscript 𝐴 1 subscript 𝐵 0 \langle A_{1}B_{0}\rangle , and ⟨ A 0 B 0 ⟩ delimited-⟨⟩ subscript 𝐴 0 subscript 𝐵 0 \langle A_{0}B_{0}\rangle , leading to a reduced violation.

| | | | | |

		( )
		187 points by \| \| \| \|

Also not directly related video if you like your mind being blown:

Especially given how our understanding of the world changed during the last 200 years, I would say we are still very much clueless. I find that exciting.

Btw, no idea why did researchers get "freedom of choice" involved.

| |

| | |

| | | |

| | | |
measuring the photons changes the results (e.g. vs. the machines measuring the photons, but scrambled so they can't recover the information). So it's definitely a property of attempting to recover the information, regardless of how it is measured or reported, which is weird, but doesn't have any sort of consciousness involving implications, because it happens to machines as well.

It's definitely worth the 10 minute watch if you want it explained to you.

| | | |
ways; and seemingly metaphysical stories or explanations that are... literal? Metaphorical? Full of borrowed BS words from point two that fall out of the math but don't "mean" anything in everyday terms? Definitely one of those until you ask a question then you're an idiot and it's another, until it's not again? Has put me off any childlike interest I once had in it. It seems fun. But I can't tell when they're serious or screwing with me. Sometimes one person claims something's serious, and they do so with authority, and another says they're screwing with me with just as much authority. I gave up.

Somewhat relatedly[0], I can't find an explanation of the Oberth Effect that makes any damn sense. Every so often I try again and leave disappointed. People are happy to provide them. There are lots of them. They attribute it to all sorts of things. Not one of them I've read makes sense.

[0] i.e. is physics, but is not quantum physics. So far as I know, anyway.

| | |

| | | |

| | | |
energy to accelerate the exhaust away from you, and you also can't really do anything to get at its gravitational energy[3].

0: Ie, thrusting your engines or crashing; things that involve g-forces; freefall.

1: That is, when most of its gravitational+kinetic energy is in kinetic form.

2: With energy mostly in gravitational form.

3: Gravitational energy is a function of where mass is at that exact moment; if you're high away from a gravity well, you have lots of energy tied up as gravitational, and no quick way to turn it into a more useful form.

| | | |

| | |

| | | |

| | |

| | | |
with the interplay with theology) I've used the following metaphor to explain how I've come to understand the idea of the supposed symbiosis between God's omniscience and our free will:

Think of God as an observer at the top of the Grand Canyon, looking down into the winding path of the river below. Humans are afloat on the river down in the canyon, unable to see what lies ahead. They can choose how to react to obstacles, for example, yet do no see them coming. God, however, sees our entire path on this metaphorical river laid out for us since birth; each of our individual choices are "perceived"[0] by him simultaneously.

[0]: Note, however, that many theologians would protest anthropomorphizing God in this way. Maimonides, as an example, says that we can speak of God as but not . He simply acts in a way that is analogous to human mercy.

| | |
ahead of time? Can He see me approaching a rock and know I will go around it on the left or right? Does He know I'll get smashed on it? If he doesn't, then that means there is a limit to His omniscience. If He does, then my "free" choices are predestined.

Furthermore, in this metaphor God doesn't just the river, He the river, and all the people on it. He laid out its twists and obstacles, with a understanding of how it would affect the humans afloat on it. Moreover, at the moment of creation, He had an unbounded freedom to create the river in any other way He saw fit. If I get smashed on a rock half way down, it's because He chose to create the river in such a way that I would get smashed on it. If He didn't know this, or didn't have a choice, then He is either not all knowing, or not all powerful.

This, for me is the fundamental problem with any theist philosophy that holds that God is both omniscient and the prime mover of creation, but still suggests concepts like free will and morality have any meaning. Not only are "our" decisions predestined, they're a direct result of another being's free will, and the concept of us then being judged on them by that same being is farcical. It's like a puppeteer putting one their puppets on trial.

| | | |

| | |
by free will, that will take more time.

| | |

That's exactly where the trouble is. In case of strict logical determinism we correct nothing because everything is predestined. However, choosing limited definitions, and restricting ourselves in comfortable contexts we can certainly avoid discomfort of the thought. Not that I have better idea, but I see clearly why non-compatibilists say "word juggling" towards compatibilists.

| | |

This statement is incorrect, and actually prove the very thing you intended to deny. It's not like adherents of C. held a plebiscite, isn't it? (And if they would, I dare to say they would be in danger of huge disappointment.) They made a choice to call an action free when it's inescapable consequence of a butterfly flapping wings millenia ago on another continent, but not free if it's e.g. equally inescapable consequence of a another human doing something recently, and closely (even if this forcing person is equally inescapably forced by a butterfly wings before). It is not, however, some sort of obvious conclusion, accepted by everybody. It's something C. philosophers prefer to call a common sense, because... well because this way we can make sense of things we do. So it feels much better.

As a side-note, your explanation of 'correction' makes perfect sense if you took the C. pill already, but doesn't make any useful proof of C. One have to accept that the only available variant of future (if we are in a purely determinist universe) still presents a free choice between correct/incorrect. Which is a circular reference to basic presumption of C.

Anyway, thank you for taking time to write the long response!

| | | |
that if that were true, then either the logic that the physical or metaphysical world runs on would be inconsistent. I suppose that isn't necessarily a deal-breaker, though.

| | |
as a mixture of any two orthogonal polarizations (a "basis"), such as "horizontal" and "vertical". "Left circular" and "right circular" are another choice.

The funny thing happens when you measure "how much" a photon is polarized into any given orientation. It appears as being polarized either in that orientation, or in the polarization complementary to what you measured. E.g., horizontal or vertical. The outcome is determined with a probability based on the actual polarization of the photon prior to your measurement. Then – the funny thing – the photon that polarization. Repeated measurement using the same basis gives the same results. Measure again with a different basis, and the game starts over again.

You can see this in the macro world with a laptop screen and two pairs of polarizing sunglasses. Using one pair of sunglasses, you should be able to block the light from the screen entirely – you are holding them perpendicular to the polarization of the screen. Place the second pair in between the first and the screen, and rotate it. At certain orientations, you will be able to see the screen! The second pair (nearest the screen) is diagonally polarized, and will "convert" the light from the screen into that polarization, before it reaches the first pair (furthest from the screen), which is orthogonal to the screen only.

(Note: Things change completely once a second photon enters the picture. It can be with the first, and their states are no longer independently describable. Measurement of one affects the pair.)

| | | |
). It's been proven that this hidden variable theory can't be true because of .

This is completely non-intuitive. See this video for a laymen's explanation: (you may also need to watch the prev. video about the EPR paradox ).

Edit: actually, this is a much better video - less technical and more visual.

| | | |
) essentially disproved hidden variables. Particles really exist in a superposition of multiple states simultaneously, and it's not because of our lack of knowledge or our frame of reference. It's a delightfully strange result.

| | |
hidden variables. The not-disproved hidden variable ideas must have explicit instantaneous action at large distances, i.e. faster-than-light communication among the hidden variables. And that is a pretty ugly thing to have; before Bell (and Aspect, maybe) one could hope that this would not be necessary.

| | |

Exactly. The universe would be rather boring if we learned everything about it during my lifetime.

| |

Here's Scott Aaronson arguing that the theoretical work underpinning this experiment is flawed.

[0]

| |
. Scott's blog post is talking about a more controversial extension to it, which combines Wigner's Friends with Hardy's Paradox to attempt to construct a reflective or meta limitation on the applicability of QM. The wiki link also discusses:

| | |

| |

In QBism, the Born rule is normative in that it tells the observer which observations to bet on, and observations are data points to update the observer’s subjective assessment of outcomes. Taking this perspective, a lot of paradoxes in QM seem to get resolved trivially. It’s controversial for sure but mathematically it’s rigorous.

| | | |
.

| |

| | |

| |

Experimental test of local observer independence

Massimiliano Proietti , Alexander Pickston , +5 authors A. Fedrizzi
Published in Science Advances 13 February 2019

98 Citations

A strong no-go theorem on the wigner’s friend paradox, events in quantum mechanics are maximally non-absolute, emergence of objective reality in an irreversible friend thought experiment, making mistakes saves the single world of the extended wigner’s friend experiment.

Highly Influenced

Locality Is Dead! Long Live Locality!

Quantum erasing the memory of wigner's friend, killing schrödinger’s cat: why macroscopic quantum superpositions are impossible in principle, hidden human variables in quantum mechanics, qubits are not observers -- a no-go theorem, decoherence framework for wigner's-friend experiments, 41 references, a no-go theorem for observer-independent facts.

Highly Influential

Observer-independence in the presence of a horizon

A suggested interpretation of the quantum theory in terms of "hidden" variables. ii, loopholes in bell inequality tests of local realism, einstein-podolsky-rosen paradox, quantum theory and the limits of objectivity, relational quantum mechanics, speakable and unspeakable in quantum mechanics: preface to the first edition, comment on healey’s “quantum theory and the limits of objectivity”, proposed experiment to test local hidden variable theories., related papers.

Showing 1 through 3 of 0 Related Papers

Environment

Experiments suggest humans can directly observe the quantum, could crossmodal senses be one key to unlock the true nature of physics.

Posted March 22, 2019

By William C. Bushell Ph.D. and Maureen Seaberg

This post is part 4 of a series.

In the earlier three installments of this series we brought attention to the fact that recently a startling, even revolutionary, new body of research in the fields of physics, biophysics, psychophysics, and neuroscience , was demonstrating unprecedented findings in the sensitivity of the human senses: vision on the level of single photons; hearing on the level of vibrations with amplitudes on the atomic scale, and discrimination of auditory time intervals in the range of millionths of a second; tactile discrimination on the scale of individual molecules; and quantum mechanically-based mechanisms of olfactory sensitivity capable of discriminating over a trillion different smells.

We noted that this body of research has emerged somewhat disparately for the most part, with neither conceptual unification, sensory-wide research coordination, nor an overarching ideological framework (although there are some notable exceptions to this generalization, and there is a new intensive scientific interest in the fields of multisensory integration, crossmodal sensory functioning, and synesthesia ).

In particular we called special attention to one of the most startling and revolutionary aspects within this new largely disparate and ad hoc scientific framework, namely, the ability of humans to directly perceive single photons of light – recently conclusively demonstrated – and the surprising proposal by leading physicists to employ and deploy this human capacity in order to investigate the profound and puzzling, but real and fundamental, phenomenon of quantum entanglement. Quantum entanglement is the phenomenon of deep and lasting connections between any two or more particles which have ever been connected, no matter how far apart they eventually will become in space or time, even on the galactic or cosmic scale. Moreover, a number of these leading physicists are proposing that a methodology and technology provided by human direct perception of quantum entanglement may actually be one of the best ways to further investigate this phenomenon, and may also actually be the best way to resolve a number of major, persistent questions in all of quantum physics, including the nature of entanglement, the so-called measurement problem and the wavefunction – in other words, the ultimate nature of the reality of the universe itself.

We also noted that the results of this recent body of research on the human vision of single photons, a natural predecessor to the ability to see the basic unit of entanglement – two entangled photons – did establish a conclusive demonstration of what science refers to as a proof of concept, in this case, that at least one human subject was clearly able to perceive a single photon of light in a series of trials following strict, rigorous study design and statistical rules. However, interviews with the scientists and supplementary materials to the studies revealed that the perception of single photons was very vague and impressionistic – yet nevertheless so far above chance that it was indeed accurate – and also, that not every subject was, in fact, able to successfully perceive the single photon. And that there was a range of performance, and demonstrated abilities, in the human subjects. Experience and training appeared to assist critically in performance.

At this point, we further noted that, apropos of these findings, there exist traditions in which practitioners of special forms of observational meditation intensively train in order to be able to directly perceive minuscule amounts, the least possible amounts, of light possible, as well as other minute and even microscopic phenomena. These traditions, and such practitioners, have existed for centuries in Asian cultures (and most likely others), and exist nowadays throughout the world, including the West, due to the spread of the teaching of the techniques. And in fact, a significant and growing body of research into their sensory-perceptual and attentional capacities has been conducted, and it has been demonstrated that among those practitioners tested, high levels of performance have been achieved (see review in Bushell 2009 and Bushell forthcoming). A number of studies have specifically investigated such practitioners’ abilities to perceive extremely minuscule amounts of light, and these studies have also shown high levels of performance. We refer to the highest performing of these practitioners as “adept perceivers,” and although none so far has been tested specifically on the capacity to perceive single photons, we have strongly advocated for their incorporation into further studies of single photon detection, and for further studies of the human capacity to perceive quantum entanglement and other aspects of the quantum nature of the universe – photon polarization, superposition, the potential appearance of light as quantized – such further studies having been eagerly proposed by a number of these leading physicists for human subjects in general.

In terms of this brief review, we should finally add that we also mentioned discovering in our earlier research (see Seaberg 2011, foreword by Bushell) that some adept traditions have placed a special emphasis on the importance of what would be described in contemporary neuroscientific terms as multisensory, cross-modal, or even synesthetic forms of perception. As we have already suggested, we believe that this multisensory orientation may well integrate the individual sense modalities, and via this integration, enhance even further the performance of each individual sense and as well as the ensemble of senses simultaneously. And in this context, the extraordinary range, magnitude, precision, accuracy, and hypersensitivity of all the senses that has recently been discovered in contemporary Western science may reveal the specific, holistic importance of this new body of discoveries for a multisensory/crossmodal orientation towards the direct perception and even direct knowledge of the nature of the phenomenal world, of the universe.

Moving specifically from these general points to the consideration of the proposed program of direct human perceptual exploration and investigation of the quantum realm, we now turn back to the focus of the beginning of this series, the recent proposition made by leading physicists that quantum entanglement and the measurement problem should be two of the primary subjects for studies based on the newly discovered level of human perception.

As already mentioned, two principle human capacities relevant for further quantum investigation that appear to have been scientifically established, then, are (a) single photon detection ( SPD ; Tinsley et al 2016) and (b) photon polarization (Ropars et al 2011; Temple et al 2015).

Importantly, cutting edge research utilizing new technological innovations as well as theoretical advances has been employing single photons and their polarization for the investigation of fundamental dimensions of quantum physics. A range of such fundamental dimensions is being investigated, and it should be noted here that the basic foundations of quantum physics are still being vigorously questioned and explored, despite the fact that many in the general public as well as in physics itself, have a sense that there is an orthodoxy which is relatively stable. This is often not the case, but is a much larger question outside the realm of this series, and should be noted by the reader.

Here, we briefly focus on several of these investigated fundamental subjects, including the Heisenberg Uncertainty Principle (HUP), which includes the question of measurement, and which will be seen to be key for understanding the so-called “measurement problem” itself, that associated with the understanding of the nature of the wavefunction.

Recently, several studies employing single photons and their polarization with manufactured technical devices have been conducted to test the famous and foundational Heisenberg Uncertainty Principle. In brief, this principle was proposed by Werner Heisenberg in the 1920s during the early, formative days of the establishment of quantum mechanics. Deriving from Heisenberg’s attempt to make sense of “anomalous” discoveries in the quantum realm that appeared to challenge classically empirical and logical principles, Heisenberg found that in order to “fit” the actual data, he was forced to propose that subatomic particles such as electrons could not be simultaneously measured with completeness or accuracy in terms of the position or the location of particles and their momentum. One or the other of these could be measured with precision at any given time, which appeared to be a completely contradictory finding in the context of classical physics, based as it was (and still is) on the fundamental principle that full knowledge of both the locations and momentums of all objects should be accessible at all times.

The history of physics and the prevalence of the quantum revolution of course now provide the basis of the physical reality in which we are living, and the equations of quantum mechanics are the most precise and accurate of any discovered or developed in history. Nevertheless, the HUP continues to be challenged within the field of quantum physics itself, and recently several experiments utilizing photons and polarization produced and controlled by sophisticated new technological devices have been used to do so. In fact, these studies have found an inconsistency in Heisenberg’s original formulation, in which there was claimed to be a measurement problem that made the determination of both location and momentum to be impossible. According to this original interpretation, any attempt at measurement on this scale of matter and energy would invariably disturb either the position (location in space) or the momentum (movement in space) of the particle, because the energy required for measurement would alter or “destabilize” the system. Hence, one of the foundational principles of quantum physics, the ultimate impossibility of complete knowledge on the subatomic scale, the most fundamental level of the universe, was in this way asserted in this version of the uncertainty principle.

The recent research mentioned above has actually demonstrated that this interpretation of the HUP is not accurate, and that this interpretation was also based on a confusion in the original formulation by Heisenberg (for clarifying discussion of this subject, Rozema et al, 2012; and see also Erhart et al 2012). In simplified terms, the recent research employs what is called “weak measurement” utilizing single photons, the energy of which is not great enough to disturb the system, achieving what is called “nondemolition” experimental outcomes. This technical procedure avoids the measurement problem that has been inextricably (but inaccurately) “interwoven” into the formalism of the HUP, but the real fundamental “uncertainty” of such particle systems (wave-particles) is based on their fundamental nature as waves, and regarding all waves there are limits to what can be known about any two noncommuting conjugates (complimentary) properties or variables at a given time, such as location and momentum; it is not a measurement problem per se, but rather an issue based on the irreducible set of properties of the structure of waves.

While there are limits to what can be known about wave phenomena at a given point in time, there are ranges to such limits. The HUP is related to other forms of “uncertainty principles,” often considered together as a class of phenomena referred to as Fourier uncertainty principles, named after a major figure in the history of science and mathematics, Joseph Fourier (18th-19th centuries). Fourier’s and much subsequent scientific and mathematical research has demonstrated that when two conjugate noncommuting properties such as the duration and frequency of a signal are considered simultaneously, the product is not smaller than a certain mathematical limit [in this case 1/(4π)].

However, recent research, which again is aimed at exploring the limits of human sensory-perceptual functioning, has demonstrated that humans are capable of actually surpassing the previously regarded limitations on human audition imposed by, in this case, the Fourier uncertainty principle, with regard to the timing and frequency of sound. Researchers at the Laboratory of Mathematical Physics of Rockefeller University demonstrated that human subjects could outperform – “beat” – the Fourier uncertainty principle limitations by over ten-fold, revealing “remarkable timing acuity” (Oppenheim & Magnasco 2013, published in a leading journal of physics and biophysics, Physical Review Letters ).

And here again in this study, we see that there is a broad range of performance in the group of human subjects and that there is an apparent key factor of training involved, in that the best performances were found in musicians, composers, conductors, and sound engineers. These professionals would be considered in the category of “expert and exceptional performance” discussed in earlier installments, the branch of cognitive neuroscience developed by the Nobel Prize winner Herbert A Simon and colleagues, a branch of science which has been adapted to the study of sensory-perceptual adepts as well (Bushell 2009). In this adaptation of the scientific framework, it has been shown that adept observational meditation training regimens appear to surpass all others with respect to intensity, extensiveness, and levels of performance, as discussed in this reference. Moreover, the adept training regimens in observational meditation under discussion here also incorporate intensive observation of sound as well (see Bushell & Thurman 2011).

Furthermore, as mentioned above and previously, these adept traditions deliberately pursue regimens which are based on multisensory integration, and preliminary evidence strongly suggests that this form of training may result in crossmodal, and even supramodal perceptual learning, and advantageous neuroplastic changes. So that the resulting temporal and spatial hyperacuity may transfer between modalities in multiple ways, and auditory hyperacuity may thereby become relevant to multimodal perception on the quantum level in many ways. In the next installments we will direct a fuller explication of this model of human sensory-perceptual potential to consider the recent research employing single photons and polarization in investigations of quantum entanglement, the nature of the wavefunction in terms of the measurement problem, and also the very recent extraordinary study of the “Wigner’s friend thought experiment,” which has produced results suggesting “that two observers can experience fundamentally different realities” in actual physical terms.

Neuroscientific and quantum physical approach to advanced Buddhist mindfulness meditation: Perceptual learning, neuroplasticity, complexity, texture, fractals, and synesthesia. A model in-progress, WC Bushell & G Thurman, Towards a Science of Consciousness, Aula Magna Hall, Stockholm, Sweden/Center for Consciousness Studies, University of Arizona, 2011.

Human Time-Frequency Acuity Beats the Fourier Uncertainty Principle, JN Oppenheim & MO Magnasco. Physical Review Letters 110, 044301: 2013.

Violation of Heisenberg’s Measurement-Disturbance Relationship by Weak Measurements, Lee A. Rozema, Ardavan Darabi, Dylan H. Mahler, Alex Hayat, Yasaman Soudagar, and Aephraim M. Steinberg. Physical Review Letters 109, 100404: 2012.

Experimental demonstration of a universally valid error–disturbance uncertainty relation in spin measurements. Jacqueline Erhart, Stephan Sponar, Georg Sulyok, Gerald Badurek, Masanao Ozawa, Yuji Hasegawa. Nature Physics, 2012; DOI: 10.1038/nphys2194.

Experimental rejection of observer-independence in the quantum world. Massimiliano Proietti, Alexander Pickston, Francesco Graffitti, Peter Barrow, Dmytro Kundys, Cyril Branciard, Martin Ringbauer, and Alessandro Fedrizzi. arXiv:1902.05080v

References for this installment that also appear in previous installments:

New Beginnings: Evidence That the Meditational Regimen Can Lead to Optimization of Perception, Attention, Cognition, and Other Functions. William C. Bushell. Annals of the New York Academy of Sciences 1172: 348-361, 2009.

Direct detection of a single photon by humans. Jonathan N. Tinsley, Maxim I. Molodtsov, Robert Prevedel, David Wartmann, Jofre Espigulé-Pons, Mattias Lauwers, Alipasha Vaziri. Nature Communications 7: 12172, 2016.

Direct Naked-Eye Detection of Chiral and Faraday Effects in White Light. G. Ropars, A. Le Floch, J. Enoch, V. Lakshminarayanan. Europhysics Letters 97 (6), 2011.

Perceiving Polarization With the Naked Eye: Characterization of Human Polarization Sensitivity. Shelby E. Temple, Juliette E. McGregor, Camilla Miles, Laura Graham, Josie Miller, Jordan Buck, Nicholas E. Scott-Samuel, and Nicholas W. Roberts. Proceedings of the Royal Society B: Biological Sciences 282(1811): 20150338, 2015.

Maureen Seaberg is a synesthete and the co-author of Struck By Genius: How a Brain Injury Made Me a Mathematical Marvel .

Find a Therapist
Find a Treatment Center
Find a Psychiatrist
Find a Support Group
Find Online Therapy
United States
Brooklyn, NY
Chicago, IL
Houston, TX
Los Angeles, CA
New York, NY
Portland, OR
San Diego, CA
San Francisco, CA
Seattle, WA
Washington, DC
Asperger's
Bipolar Disorder
Chronic Pain
Eating Disorders
Passive Aggression
Personality
Goal Setting
Positive Psychology
Stopping Smoking
Low Sexual Desire
Relationships
Child Development
Self Tests NEW
Therapy Center
Diagnosis Dictionary
Types of Therapy

It’s increasingly common for someone to be diagnosed with a condition such as ADHD or autism as an adult. A diagnosis often brings relief, but it can also come with as many questions as answers.

Emotional Intelligence
Gaslighting
Affective Forecasting
Neuroscience

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

View all journals
Explore content
About the journal
Publish with us
Sign up for alerts
Published: 06 September 2022

Wigner’s friend and relational objectivity

Časlav Brukner 1

Nature Reviews Physics volume 4 , pages 628–630 ( 2022 ) Cite this article

1061 Accesses

5 Citations

4 Altmetric

Metrics details

Quantum information
Quantum mechanics

The ‘Wigner’s friend’ thought experiment illustrates the puzzling nature of quantum measurement. Časlav Brukner discusses how recent results suggest that in quantum theory the objectivity of measurement outcomes is relative to observation and observer.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

What Does ‘(Non)-absoluteness of Observed Events’ Mean?

Emily Adlam

Foundations of Physics Open Access 10 January 2024

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 12 digital issues and online access to articles

92,52 € per year

only 7,71 € per issue

Buy this article

Purchase on SpringerLink
Instant access to full article PDF

Prices may be subject to local taxes which are calculated during checkout

Wigner, E. P. Remarks on the mind-body question. In The Scientist Speculates (ed. Good, I. J.) 284–302 (Heinemann, 1961).

Brukner, Č. On the quantum measurement problem. In Quantum[Un]Speakables II: Half a Century of Bell’s Theorem (eds Bertlmann, R. & Zeilinger, A.) 95–117 (Springer, 2017).

Frauchiger, D. & Renner, R. Quantum theory cannot consistently describe the use of itself. Nat. Commun. 9 , 3711 (2018).

Article ADS Google Scholar

Brukner, Č. A no-go theorem for observer-independent facts. Entropy 20 , 350 (2018).

Article ADS MathSciNet Google Scholar

Bong, K. W. et al. A strong no-go theorem on the Wigner’s friend paradox. Nat. Phys. 16 , 1199–1205 (2020).

Article Google Scholar

Proietti, M. et al. Experimental test of local observer independence. Sci. Adv. 5 , eaaw9832 (2019).

Fuchs, C. A. & Schack, R. Quantum-Bayesian coherence. Rev. Mod. Phys. 85 , 1693 (2013).

Rovelli, C. Relational quantum mechanics. Int. J. Theor. Phys. 35 , 1637–1678 (1996).

Article MathSciNet Google Scholar

Healey, R. The Quantum Revolution in Philosophy (Oxford University Press, 2017).

Cavalcanti, E. G. The view from a Wigner bubble. Found. Phys. 51 , 39 (2021).

Download references

Author information

Authors and affiliations.

Institute for Quantum Optics and Quantum Information, Austrian Academy of Sciences and Faculty of Physics, University of Vienna, Vienna, Austria

Časlav Brukner

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Časlav Brukner .

Ethics declarations

Competing interests.

The author declares no competing interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Brukner, Č. Wigner’s friend and relational objectivity. Nat Rev Phys 4 , 628–630 (2022). https://doi.org/10.1038/s42254-022-00505-8

Download citation

Published : 06 September 2022

Issue Date : October 2022

DOI : https://doi.org/10.1038/s42254-022-00505-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

Explore articles by subject
Guide to authors
Editorial policies

Information

Author Services

Initiatives

You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.

All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .

Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.

Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.

Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.

Original Submission Date Received: .

Active Journals
Find a Journal
Journal Proposal
Proceedings Series
For Authors
For Reviewers
For Editors
For Librarians
For Publishers
For Societies
For Conference Organizers
Open Access Policy
Institutional Open Access Program
Special Issues Guidelines
Editorial Process
Research and Publication Ethics
Article Processing Charges
Testimonials
Preprints.org
SciProfiles
Encyclopedia

Article Menu

Subscribe SciFeed
Recommended Articles
Author Biographies
Google Scholar
on Google Scholar
Table of Contents

Find support for a specific problem in the support section of our website.

Please let us know what you think of our products and services.

Visit our dedicated information section to learn more about MDPI.

JSmol Viewer

Active disturbance rejection control combined with improved model predictive control for large-capacity hybrid energy storage systems in dc microgrids.

1. Introduction

2. the structure of typical dc microgrids and traditional control strategies, 2.1. power allocation between different energy storage systems of hess, 2.2. pi double closed-loop control, 3. active disturbance rejection control combined with improved mpc of large-capacity hess in dc microgrids, 3.1. active disturbance rejection control of outer voltage control loop, 3.2. improved model predictive control of the inner current control loop.

Model the converters and identify all switching modes. Predict behaviors of the controlled variables (e.g., voltages, currents) under various switching modes.
Define the evaluation function according to the system model and control variables and obtain values of the predicted evaluation function.
Choose the optimal switching state corresponding to the minimized evaluation function.

3.3. Designing a Secondary DC Bus Voltage Compensator in the Condition of Voltage Drops

3.4. design procedure of proposed control strategies of n parallel battery converters and the supercapacitor converter in dc microgrids, 4. simulation verifications, 4.1. validations of improved mpc, 4.2. simulation verifications of the proposed dc bus voltage compensator, 4.3. validations of adrc and improved mpc, 5. experimental results, 5.1. verifications of the proposed dc bus voltage compensator, 5.2. validations of adrc combined with improved mpc, 6. conclusions, author contributions, data availability statement, conflicts of interest.

Zhang, Q.; Zeng, Y.; Liu, Y.; Zhuang, X.; Zhang, H.; Hu, W.; Guo, H. An improved distributed cooperative control strategy for multiple energy storages parallel in islanded DC microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2022 , 10 , 455–468. [ Google Scholar ] [ CrossRef ]
Li, Z.; Wang, B.; Xian, L.; Zhang, M.; Xu, Q. Decentralized Active Disturbance Rejection Control for Hybrid Energy Storage System in DC Microgrid. IEEE Trans. Ind. Electron. 2024 , 71 , 14232–14243. [ Google Scholar ] [ CrossRef ]
Cui, J.; Tian, G.; Liu, G.; Wu, Y.; Guo, Z. Research on coordinated control strategy of isolated DC microgrid with PV/hybrid energy storage. Energy Rep. 2022 , 8 (Suppl. 10), 893–899. [ Google Scholar ] [ CrossRef ]
Zhou, Q.; Jin, J.; Yang, R. Static state power smoothing and transient power quality enhancement of a DC microgrid based on multi-function SMES/battery distributed hybrid energy storage system. Energy Rep. 2022 , 8 (Suppl. 13), 44–51. [ Google Scholar ] [ CrossRef ]
Zheng, Z.; Chen, X.; Hu, W.; Wang, Y.; Zong, Y.; Huang, C.; Ni, F. Dual Model Predictive Controlled Hybrid Energy Storage System for Naval DC Microgrids. IEEE Trans. Transp. Electrif. 2023 , 9 , 156–168. [ Google Scholar ] [ CrossRef ]
Liu, X.; Suo, Y.; Song, X.; Zhou, J.; Qu, Y. Large-Signal Stabilization Method for Islanded DC Microgrids Considering Battery and Supercapacitor Hybrid Energy Storage Systems. Electronics 2022 , 11 , 2823. [ Google Scholar ] [ CrossRef ]
Mitra, S.K.; Karanki, S.B. An SOC Based Adaptive Energy Management System for Hybrid Energy Storage System Integration to DC Grid. IEEE Trans. Ind. Appl. 2023 , 59 , 1152–1161. [ Google Scholar ] [ CrossRef ]
Liu, X.; Suo, Y.; Zhang, Z.; Song, X.; Zhou, J. A New Model Predictive Current Control Strategy for Hybrid Energy Storage System Considering the SOC of the Supercapacitor. IEEE J. Emerg. Sel. Top. Power Electron. 2023 , 11 , 325–338. [ Google Scholar ] [ CrossRef ]
Zhao, X.; Zhang, Y.; Cui, X.; Wan, L.; Qiu, J.; Shang, E.; Zhang, Y.; Zhao, H. Wavelet Packet-Fuzzy Optimization Control Strategy of Hybrid Energy Storage Considering Charge–Discharge Time Sequence. Sustainability 2023 , 15 , 10412. [ Google Scholar ] [ CrossRef ]
Xiang, C.; Cheng, Q.; Zhu, Y.; Zhao, H. Sliding Mode Control of Ship DC Microgrid Based on an Improved Reaching Law. Energies 2023 , 16 , 1051. [ Google Scholar ] [ CrossRef ]
Ahmed, K.; Hussain, I.; Seyedmahmoudian, M.; Stojcevski, A.; Mekhilef, S. Voltage Stability and Power Sharing Control of Distributed Generation Units in DC Microgrids. Energies 2023 , 16 , 7038. [ Google Scholar ] [ CrossRef ]
Elnady, A.; Noureldin, A.; Adam, A.A. Improved Synergetic Current Control for Grid-connected Microgrids and Distributed Generation Systems. J. Mod. Power Syst. Clean Energy 2022 , 10 , 1302–1313. [ Google Scholar ] [ CrossRef ]
Bonfiglio, A.; Procopio, R.; Rosini, A.; Incremona, G.P.; Ferrara, A. A Comprehensive Sliding Mode Approach for Photovoltaic-Storage Islanded Microgrids. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; pp. 1–5. [ Google Scholar ]
Al Sumarmad, K.A.; Sulaiman, N.; Wahab, N.I.A.; Hizam, H. Energy Management and Voltage Control in Microgrids Using Artificial Neural Networks, PID, and Fuzzy Logic Controllers. Energies 2022 , 15 , 303. [ Google Scholar ] [ CrossRef ]
Yuan, L.; Xiu, C.; Ma, X. Sliding mode control strategy for microgrid inverter systems. J. Power Electron. 2023 , 23 , 821–831. [ Google Scholar ] [ CrossRef ]
Zhang, M.; Xu, Q.; Zhang, C.; Nordström, L.; Blaabjerg, F. Decentralized Coordination and Stabilization of Hybrid Energy Storage Systems in DC Microgrids. IEEE Trans. Smart Grid 2022 , 13 , 1751–1761. [ Google Scholar ] [ CrossRef ]
Kim, S.-K.; Park, C.R.; Kim, J.-S.; Lee, Y.I. A stabilizing model predictive controller for voltage regulation of a DC/DC boost converter. IEEE Trans. Control. Syst. Technol. 2014 , 22 , 2016–2023. [ Google Scholar ] [ CrossRef ]
Qiu, C.; Li, Z.; Tan, Q.; Huang, J.; Wang, D. Hybrid Model Linearization Predictive Control for DC Bus Stabilization in Spacecraft Combined Power System. IEEE J. Emerg. Sel. Top. Power Electron. 2022 , 10 , 5345–5356. [ Google Scholar ] [ CrossRef ]
Peng, W.; Chen, Q.; Manandhar, U.; Wang, B.; Rodriguez, J. Event-Triggered Model Predictive Control for the Inverter of a Grid-Connected Microgrid With a Battery-Supercapacitor HESS. IEEE J. Emerg. Sel. Top. Power Electron. 2023 , 11 , 5540–5552. [ Google Scholar ] [ CrossRef ]
Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Adaptive Active Disturbance Rejection Control for Uncertain Current Ripples Suppression of PMSM Drives. IEEE Trans. Ind. Electron. 2024 , 71 , 2320–2331. [ Google Scholar ] [ CrossRef ]
Du, Y.; Cao, W.; She, J. Analysis and Design of Active Disturbance Rejection Control With an Improved Extended State Observer for Systems With Measurement Noise. IEEE Trans. Ind. Electron. 2023 , 70 , 855–865. [ Google Scholar ] [ CrossRef ]
Long, B.; Zeng, W.; Rodríguez, J.; Garcia, C.; Guerrero, J.M.; Chong, K.T. Stability Enhancement of Battery-Testing DC Microgrid: An ADRC-Based Virtual Inertia Control Approach. IEEE Trans. Smart Grid 2022 , 13 , 4256–4268. [ Google Scholar ] [ CrossRef ]
Shan, Z.; Wang, Y.; Liu, X.; Wei, C. Fuzzy Automatic Disturbance Rejection Control of Quadrotor UAV Based on Improved Whale Optimization Algorithm. IEEE Access 2023 , 11 , 69117–69130. [ Google Scholar ] [ CrossRef ]
Tao, L.; Wang, P.; Wang, Y.; Ma, X.; Shi, H.; Yang, S. Automatic-Optimization ADRC-Based Disturbance Rejection Method for Low Voltage Interface Converter in Microgrid. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [ Google Scholar ]
Dai, T.; Mao, J.; Ding, Y.; Yin, C.; Zhang, X. Bus voltage stability control of the distributed photovoltaic and energy storage DC microgrid based on ADRC. In Proceedings of the 2021 IEEE International Conference on Recent Advances in Systems Science and Engineering (RASSE), Shanghai, China, 12–14 December 2021; pp. 1–7. [ Google Scholar ]
Hai, T.; Liu, Y.; Wang, J.; Lu, J. Control Strategy of Photovoltaic Hybrid Energy Storage System Based on Model Predictive Control. J. Power Supply 2024 , 1–12. [ Google Scholar ]
Nguyen, H.D.; Tran, L.T.H.; Nguyen, T.D.; Pham, M.D. Load Profile-Based Setpoint Design for Piecewise Droop Controller to Mitigate Current Sharing Error in Dual Active Bridge System. IEEJ Trans. Electr. Electron. Eng. 2024 , 19 . [ Google Scholar ] [ CrossRef ]
Chang, S.; Wang, C.; Luo, X.; Guan, X. Distributed predefined-time secondary control under directed networks for DC microgrids. Appl. Energy 2024 , 374 , 123993. [ Google Scholar ] [ CrossRef ]
Li, X.; Wang, M.; Jiang, W.; Dong, C.; Xu, Z.; Wu, X. An Autonomous Finite-Time Backstepping Control for Decentralized Automatic Power Sharing of Hybrid Energy Storage Systems in DC Microgrids. IEEE Trans. Smart Grid 2024 , 15 , 3348–3360. [ Google Scholar ] [ CrossRef ]
Lasabi, O.; Swanson, A.; Jarvis, L.; Aluko, A.; Brown, M. Enhanced Distributed Non-Linear Voltage Regulation and Power Apportion Technique for an Islanded DC Microgrid. Appl. Sci. 2023 , 13 , 8659. [ Google Scholar ] [ CrossRef ]
Xing, L.; Qi, Y.; Liu, X.-K.; Wen, C.; Liu, M.; Tian, Y.-C. Discrete-Time Distributed Secondary Control for DC Microgrids via Virtual Voltage Drop Averaging. IEEE Trans. Sustain. Energy 2023 , 14 , 272–282. [ Google Scholar ] [ CrossRef ]
Zeng, Y.; Zhang, Q.; Liu, Y.; Zhuang, X.; Guo, H. Hierarchical Cooperative Control Strategy for Battery Storage System in Islanded DC Microgrid. IEEE Trans. Power Syst. 2022 , 37 , 4028–4039. [ Google Scholar ] [ CrossRef ]
Zhuo, S.; Ma, Y.; Liu, X.; Zhang, R.; Jin, S.; Huangfu, Y. Quasi-Resonant-Based ADRC for Bus Voltage Regulation of Hybrid Fuel Cell System. IEEE Trans. Ind. Electron. 2024 , 1–10. [ Google Scholar ] [ CrossRef ]
Li, J.; You, H.; Liu, S.; Li, X.; Ding, Z.; Zou, F. Active disturbance rejection distributed secondary control for DC microgrids. High Volt. 2024 , 9 , 241–251. [ Google Scholar ] [ CrossRef ]

Click here to enlarge figure

Switching Modes	Battery Converter		Supercapacitor Converter
Switching Modes	SW	SW	SW	SW
1	1	0	1	0
2	1	0	0	1
3	0	1	1	0
4	0	1	0	1

Switching Modes	Battery Converter		Supercapacitor Converter		Switches in on State
Switching Modes	SW	SW	SW	SW	n
1	1	0	1	0	2
2	1	0	0	1	2
3	1	0	0	0	1
4	0	1	1	0	2
5	0	1	0	1	2
6	0	1	0	0	1
7	0	0	1	0	1
8	0	0	0	1	1
9	1	0	0	0	0

Parameters	Value
DC bus voltage	400 V
	160 V
	160 V
	160 V
Variable	200 V
Droop coefficient of the first battery converter	0.5
Droop coefficient of the second battery converter	0.5
Bus capacitor	3000 μF
The PV generation power	4100 W
Initial power of the variable load	3100 W

Parameter	Value
	64 V
Battery voltage v	35 V
Battery voltage v	35 V
Supercapacitor terminal voltage v	24 V
Variable load voltage v	48 V
Bus capacitors	2.2 × 10 F
Initial power of the variable load	80 W

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

Liu, X.; Chen, J.; Suo, Y.; Song, X.; Ju, Y. Active Disturbance Rejection Control Combined with Improved Model Predictive Control for Large-Capacity Hybrid Energy Storage Systems in DC Microgrids. Appl. Sci. 2024 , 14 , 8617. https://doi.org/10.3390/app14198617

Liu X, Chen J, Suo Y, Song X, Ju Y. Active Disturbance Rejection Control Combined with Improved Model Predictive Control for Large-Capacity Hybrid Energy Storage Systems in DC Microgrids. Applied Sciences . 2024; 14(19):8617. https://doi.org/10.3390/app14198617

Liu, Xinbo, Jiangsha Chen, Yongbing Suo, Xiaotong Song, and Yuntao Ju. 2024. "Active Disturbance Rejection Control Combined with Improved Model Predictive Control for Large-Capacity Hybrid Energy Storage Systems in DC Microgrids" Applied Sciences 14, no. 19: 8617. https://doi.org/10.3390/app14198617

Article Metrics

Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals

COMMENTS

Experimental rejection of observer-independence in the quantum world
Quantum Physics. Experimental rejection of observer-independence in the quantum world. The scientific method relies on facts, established through repeated measurements and agreed upon universally, independently of who observed them. In quantum mechanics, the objectivity of observations is not so clear, most dramatically exposed in Eugene Wigner ...
Experimental rejection of observer-independence in the quantum world
While observer-independence has long remained inaccessible to empirical investigation, recent no-go-theorems construct an extended Wigner's friend scenario with four entangled observers that allows us to put it to the test. In a state-of-the-art 6-photon experiment, we here realise this extended Wigner's friend scenario, experimentally ...
Experimental rejection of observer-independence in the quantum world
Request PDF | Experimental rejection of observer-independence in the quantum world | The scientific method relies on facts, established through repeated measurements and agreed upon universally ...
Experimental rejection of observer-independence in the quantum world
Implementing the experiment with more complex observers would not necessarily lead to new insights into the speciﬁc issue of observer-independence in quantum theory. It would however serve to show that quantum mechanics still holds at larger scales, ruling out alternative (collapse) models [16].
A quantum experiment suggests there's no such thing as objective
Physicists have long suspected that quantum mechanics allows two observers to experience different, conflicting realities. ... Experimental Rejection of Observer-Independence ... who went to ...
PDF arXiv:1902.05080v1 [quant-ph] 13 Feb 2019
Experimental rejection of observer-independence in the quantum world Massimiliano Proietti, 1Alexander Pickston, Francesco Graﬃtti, Peter Barrow,1 Dmytro Kundys,1 Cyril Branciard,2 Martin Ringbauer,1,3 and Alessandro Fedrizzi1 1Scottish Universities Physics Alliance (SUPA), Institute of Photonics and Quantum Sciences, School of Engineering and Physical Sciences, Heriot-Watt University ...
Refuting Observer-Independence in Quantum Theory
When Eugene Wigner conceived his Gedanken experiment in 1961 [1], he argued that in quantum theory two observers, Wigner and his friend, can experience two fundamentally different descriptions of reality. Yet, only six decades later, this question has been rigorously tackled independently by Brukner [2] and Frauchiger and Renner [3], leveraging on the Bell's theorem and on the Hardy's Paradox ...
A No-Go Theorem for Observer-Independent Facts
3. "Freedom of choice". The choice of measurement settings is statistically independent from the rest of the experiment. 4. "Observer-independent facts". One can jointly assign truth values to the propositions about observed outcomes ("facts") of different observers (as specified in the postulate above).
PDF Experimental rejection of observer-independence in the quantum world
Experimental rejection of observer-independence in the quantum world (30'+10') Tuesday, 30 April 2019 15:40 (0:40) Content Summary Presenter(s) : A. FEDRIZZI (Heriot-Watt University Edinburgh, UK) Session Classi cation : DAY II. Created Date:
Experimental rejection of observer-independence in the quantum world
This result lends considerable strength to interpretations of quantum theory already set in an observer-dependent framework and demands for revision of those which are not.}, added-at = {2019-04-09T14:43:35.000+0200}, author = {Proietti, Massimiliano and Pickston, Alexander and Graffitti, Francesco and Barrow, Peter and Kundys, Dmytro and ...
PDF arXiv:1902.05080v2 [quant-ph] 4 Nov 2019
Experimental test of local observer-independence Massimiliano Proietti, 1Alexander Pickston, Francesco Graﬃtti, Peter Barrow,1 Dmytro Kundys,1 Cyril Branciard,2 Martin Ringbauer,1,3 and Alessandro Fedrizzi1 1Scottish Universities Physics Alliance (SUPA), Institute of Photonics and Quantum Sciences, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh EH14 4AS, UK.
PDF Louis Marchildon arXiv:1910.12253v1 [quant-ph] 27 Oct 2019
unitary quantum mechanics. Since A0 and A1 do not commute, they are not expected to have simultaneous values. Proietti et al. [2] interpret their result as an "experimental rejection of observer-independence." If one observer registers a value, the other doesn't. To reach this conclusion, they are careful to deﬁne an observer as "any ...
Experimental test of local observer independence
According to quantum theory, Wigner must describe the friend s measurement as a unitary interaction that leaves the photon ' and the friends record in the entangled state (with implicit tensor ' products) 1 1. ± photon is. ffiffiffi2 ð∣h〉 ∣v〉Þ→ p ffiffiffi2 ð∣h〉∣" h"〉. ± ∣v〉∣"photon is ± v"〉Þ≕∣F ...
Paper Review: Experimental Rejection of Observer-independence in the
"Experimental rejection of observer-independence in the quantum world" Uh-oh. This sounds like a case where maybe the media are actually reporting accurately on the science—the title would certainly suggest that the scientists believe their experiment rejects objective reality, or something like that.
Experimental test of local observer independence
The observer's role as final arbiter of universal facts was imperiled by the advent of 20th century science.In relativity, previously absolute observations are now relative to moving reference frames; in quantum theory, all physical processes are continuous and deterministic, except for observations, which are proclaimed to be instantaneous and probabilistic.
[1902.05080] Experimental test of local observer-independence
The observer's role as final arbiter of universal facts Popper was imperilled by the advent of 20 th th {}^{\textrm{th}} century science. In relativity, previously absolute observations are now relative to moving reference frames; in quantum theory, all physical processes are continuous and deterministic, except for observations, which are proclaimed to be instantaneous and probabilistic.
Experimental rejection of observer-independence in the quantum world
Experimental rejection of observer-independence in the quantum world (arxiv.org) 187 points by lisper 7 months ago | hide | past ... So an "experimental demonstration" of their setup—by which one really means an experimental demonstration of Hardy's experiment, since the Frauchiger-Renner one would require superposed conscious observers ...
Experimental test of local observer independence
2018. TLDR. A no-go theorem for observer-independent facts, which would be common both for Wigner and the friend is derived and is analyzed in the context of a newly-derived theorem arXiv:1604.07422, where Frauchiger and Renner prove that "single-world interpretations of quantum theory cannot be self-consistent". Expand.
Experimental Rejection of Observer-Independence in the Quantum World
Only if you assume locality holds fast. This subs ideas already reject the idea of locality and much of quantum research is leaning the same way (quantum eraser experiment). To me, this only corroborates a non local observer independent universe, not disproves it. What this experiment does is violate the bell inequality.
‪Peter Barrow‬
Experimental quantum conference key agreement. M Proietti, J Ho, F Grasselli, P Barrow, M Malik, A Fedrizzi ... Experimental rejection of observer-independence in the quantum world. arXiv e-prints, page. M Proietti, A Pickston, F Graffitti, P Barrow, D Kundys, C Branciard, ... arXiv preprint arXiv:1902.05080, 2019. 2: 2019: Experimental test of ...
[1902.09028] Observer-independence in the presence of a horizon
Observer-independence in the presence of a horizon. Ian T. Durham. In the famous thought experiment known as Wigner's friend, Wigner assigns an entangled state to the composite quantum system consisting of his friend and her observed system. In the context of this thought experiment, Brukner recently derived a no-go theorem for observer ...
Experiments Suggest Humans Can Directly Observe the Quantum
Experimental rejection of observer-independence in the quantum world. Massimiliano Proietti, Alexander Pickston, Francesco Graffitti, Peter Barrow, Dmytro Kundys, Cyril Branciard, Martin Ringbauer ...
Wigner's friend and relational objectivity
The results can be interpreted to imply that in quantum physics the objectivity of facts is not absolute, but only relative to the observation and the observer. The objective world
Active Disturbance Rejection Control Combined with Improved Model
In DC microgrids, a large-capacity hybrid energy storage system (HESS) is introduced to eliminate variable fluctuations of distributed source powers and load powers. Aiming at improving disturbance immunity and decreasing adjustment time, this paper proposes active disturbance rejection control (ADRC) combined with improved MPC for n + 1 parallel converters of large-capacity hybrid energy ...

Subscribe to the PwC Newsletter

Add a new code entry for this paper

Remove a task

Code Edit Add Remove Mark official

Experimental rejection of observer-independence in the quantum world

No file available

Experimental rejection of observer-independence in the quantum world

Related Papers

RELATED PAPERS

A quantum experiment suggests there’s no such thing as objective reality

Keep Reading

Why OpenAI’s new model is such a big deal

A controversial Chinese CRISPR scientist is still hopeful about embryo gene editing. Here’s why.

Meet the radio-obsessed civilian shaping Ukraine’s drone defense

Two Nobel Prize winners want to cancel their own CRISPR patents in Europe

Stay connected

IEEE Account

Purchase Details

Experimental rejection of observer-independence in the quantum world

Paper Review: Experimental Rejection of Observer-independence in the Quantum World

Share this:

Leave a comment Cancel reply

Experimental test of local observer-independence

Introduction.—

Discussion.—

Supplementary materials

Measurement protocol.—

Error analysis.—

Towards a loophole-free “Bell-Wigner” test.—

Alternative observables A 0 , B 0 subscript 𝐴 0 subscript 𝐵 0 A_{0},B_{0} .—

Alternative measurement protocol for A 0 , B 0 subscript 𝐴 0 subscript 𝐵 0 A_{0},B_{0} .—

Experimental test of local observer independence

98 Citations

Locality Is Dead! Long Live Locality!

Observer-independence in the presence of a horizon

Environment

Wigner’s friend and relational objectivity

Relevant articles

What Does ‘(Non)-absoluteness of Observed Events’ Mean?

Access options

Author information

Corresponding author

Ethics declarations

Rights and permissions

About this article

Share this article

Quick links

Information

Initiatives

Article Menu

JSmol Viewer

1. Introduction

3.3. Designing a Secondary DC Bus Voltage Compensator in the Condition of Voltage Drops

Share and Cite

Article Metrics

COMMENTS