ordinal logistic regression hypothesis

Companion to BER 642: Advanced Regression Methods

Chapter 12 ordinal logistic regression, 12.1 introduction to ordinal logistic regression.

Ordinal Logistic Regression is used when there are three or more categories with a natural ordering to the levels, but the ranking of the levels do not necessarily mean the intervals between them are equal.

Examples of ordinal responses could be:

The effectiveness rating of a college course on a scale of 1-5

Levels of flavors for hot wings

Medical condition (e.g., good, stable, serious, critical)

Diseases can be graded on scales from least severe to most severe

Survey respondents choose answers on scales from strongly agree to strongly disagree

Students are graded on scales from A to F

12.2 Cumulative Probability

When response categories are ordered, the logits can utilize the ordering. You can modify the binary logistic regression model to incorporate the ordinal nature of a dependent variable by defining the probabilities differently.

Instead of considering the probability of an individual event, you consider the probabilities of that event and all events that are ordered before it.

A cumulative probability for \(Y\) is the probability that \(Y\) falls at or below a particular point. For outcome category \(j\) , the cumulative probability is: \[P(Y \leq j)=\pi_{1}+\ldots+\pi_{j}, \mathrm{j}=1, \ldots, \mathrm{J}\] where \(𝜋_𝑗\) is the probability to chose category \(j\)

12.3 Link Function

The link function is the function of the probabilities that results in a linear model in the parameters.

Five different link functions are available in the Ordinal Regression procedure in SPSS: logit, complementary log-log, negative log-log, probit, and Cauchit (inverse Cauchy)

The symbol \(ϒ\) (gamma) represents the probability that the event occurs. Remember that in ordinal regression, the probability of an event is redefined in terms of cumulative probabilities.

Table 1. The link function

Probit and logit models are reasonable choices when the changes in the cumulative probabilities are gradual. If there are abrupt changes, other link functions should be used.

The complementary log-log link may be a good model when the cumulative probabilities increase from 0 fairly slowly and then rapidly approach 1.

If the opposite is true, namely that the cumulative probability for lower scores is high and the approach to 1 is slow, the negative log-log link may describe the data.

12.4 Prepare the Data

Data Information (Agresti (1996), Table 6.9, p. 186)

Data set (impairment.sav) comes from a study of mental health for a random sample of adult residents of Alachua County, Florida. Mental impairment is ordinal, with categories (1 = well, 2 = mild symptom formation, 3 = moderate symptom formation, 4 = impaired).

The study related Y = mental impairment to two explanatory variables. The life events is a composite measure of the number and severity of important life events such as birth of child, new job, divorce, or death in family that occurred to the subject within the past three years. In this sample it has a mean of 4.3 and standard deviation of 2.7. Socioeconomic status (SES) is measured here as binary (0 = low & 1 = high).

12.5 Descriptive Analysis

12.6 run the ordinal logistic regression model using mass package, 12.7 check the overall model fit.

Before proceeding to examine the individual coefficients, you want to look at an overall test of the null hypothesis that the location coefficients for all of the variables in the model are 0.

You can base this on the change in log-likelihood when the variables are added to a model that contains only the intercept. The change in likelihood function has a chi-square distribution even when there are cells with small observed and predicted counts.

From the table, you see that the chi-square is 9.944 and p = .007. This means that you can reject the null hypothesis that the model without predictors is as good as the model with the predictors.

12.8 Check the model fit information

12.9 compute a confusion table and misclassification error (r exclusive).

The confusion matrix shows the performance of the ordinal logistic regression model. For example, it shows that, in the test dataset, 6 times category “well” is identified correctly. Similarly, 4 times category “mild” and 5 times category "" is identified correctly.

Using the confusion matrix, we can find that the misclassification error for our model is 62.5%.

12.10 Measuring Strength of Association (Calculating the Pseudo R-Square)

There are several R^2-like statistics that can be used to measure the strength of the association between the dependent variable and the predictor variables.

They are not as useful as the statistic in multiple regression, since their interpretation is not straightforward.

For this example, there is the relationship of 23.6% between independent variables and dependent variable based on Nagelkerke’s R^2.

12.11 Parameter Estimates

• Please check the Slides 22 to Slides 26 to learn how to interpret the estimates

12.12 Calculating Expected Values

12.13 references.

Agresti, A. (1996). An introduction to categorical data analysis. New York, NY: Wiley & Sons. Chapter 6.

Norusis, M. (2012). IBM SPSS Statistics 19 Advanced statistical procedures companion. Pearson.

Data files from http://www.ats.ucla.edu/stat/spss/dae/mlogit.htm and Agresti (1996).

Lecture 3 - Generalized Linear Models: Ordinal Logistic Regression

Lecture 3 - generalized linear models: ordinal logistic regression #, today’s learning goals #.

By the end of this lecture, you should be able to:

Outline the modelling framework of the Ordinal Logistic regression.

Explain the concept of proportional odds.

Fit and interpret Ordinal Logistic regression.

Use the Ordinal Logistic regression for prediction.

Loading Libraries #

1. the need for an ordinal model #.

We will continue with Regression Analysis on categorical responses . Recall that a discrete response is considered as categorical if it is of factor-type with more than two categories under the following subclassification:

Nominal. We have categories that do not follow any specific order—for example, the type of dwelling according to the Canadian census: single-detached house , semi-detached house , row house , apartment , and mobile home .

Ordinal. The categories, in this case, follow a specific order—for example, a Likert scale of survey items: strongly disagree , disagree , neutral , agree , and strongly agree .

The previous Multinomial Logistic model, from Lecture 2 - Generalized Linear Models: Model Selection and Multinomial Logistic Regression , is unsuitable for ordinal responses . For example, suppose one does not consider the order in the response levels when necessary. In that case, we might risk losing valuable information when making inference or predictions . This valuable information is in the ordinal scale, which could be set up via cumulative probabilities (recall DSCI 551 concepts).

Therefore, the ideal approach is an alternative logistic regression that suits ordinal responses. Hence, the existence of the Ordinal Logistic regression model . Let us expand the regression mindmap as in Fig. 8 to include this new model. Note there is a key characteristic called proportional odds which is reflected on the data modelling framework .

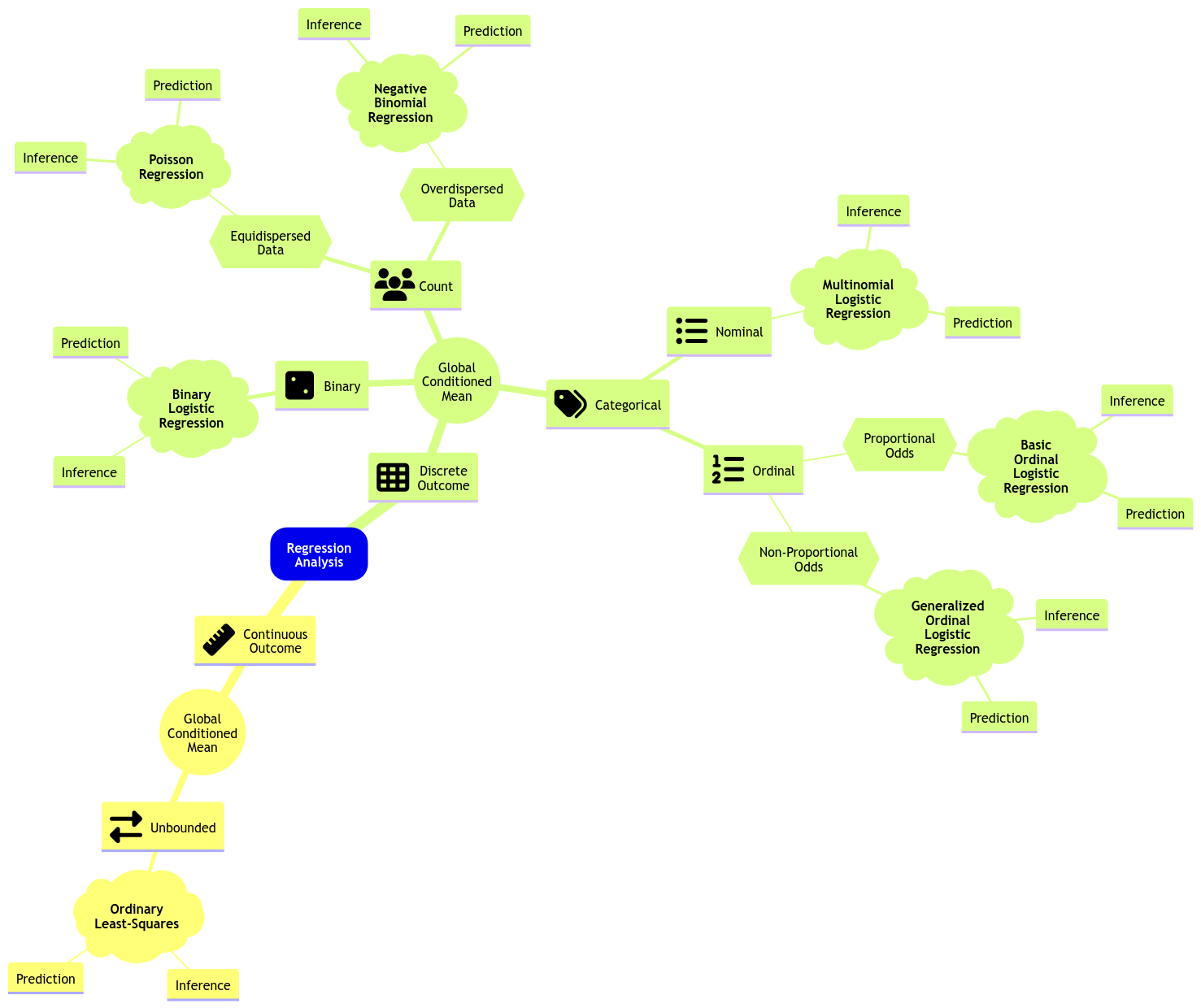
Fig. 8 Expanded regression modelling mind map. #

2. College Juniors Dataset #

To illustrate the use of this generalized linear model (GLM), let us introduce an adequate dataset.

The College Juniors Dataset

The data frame college_data was obtained from the webpage of the UCLA Statistical Consulting Group .

This dataset contains the results of a survey applied to \(n = 400\) college juniors regarding the factors that influence their decision to apply to graduate school.

The dataset contains the following variables:

decision : how likely the student will apply to graduate school, a discrete and ordinal response with three increasing categories ( unlikely , somewhat likely , and very likely ).

parent_ed : whether at least one parent has a graduate degree, a discrete and binary explanatory variable ( Yes and No ).

GPA : the student’s current GPA, a continuous explanatory variable .

In this example, variable decision will be our response of interest. However, before proceeding with our regression analysis. Let us set it up as an ordered factor via function as.ordered() .

• 'somewhat likely'
• 'very likely'

Main Statistical Inquiries

Let us suppose we want to assess the following:

Is decision statistically related to parent_ed and GPA ?

How can we interpret these statistical relationships ( if there are any! )?

3. Exploratory Data Analysis #

Let us plot the data first. Since decision is a discrete ordinal response , we have to be careful about the class of plots we are using regarding exploratory data analysis (EDA).

To explore visually the relationship between decision and GPA , we will use the following side-by-side plots:

Violin plots.

The code below creates side-by-side boxplots and violin plots, where GPA is on the \(y\) -axis, and all categories of decision are on the \(x\) -axis. The side-by-side violin plots show the mean of GPA by decision category in red points.

Now, how can we visually explore the relationship between decision and parent_ed ?

In the case of two categorical explanatory variables, we can use stacked bar charts. Each bar will show the percentages (depicted on the \(y\) -axis) of college students falling on each ordered category of decision with the categories found in parent_ed on the \(x\) -axis. This class of bars will allow us to compare both levels of parent_ed in terms of the categories of decision .

First of all, we need to do some data wrangling. The code below obtains the proportions for each level of decision conditioned on the categories of parent_ed . If we add up all proportions corresponding to No or Yes , we will obtain 1.

Then, we code the corresponding plot:

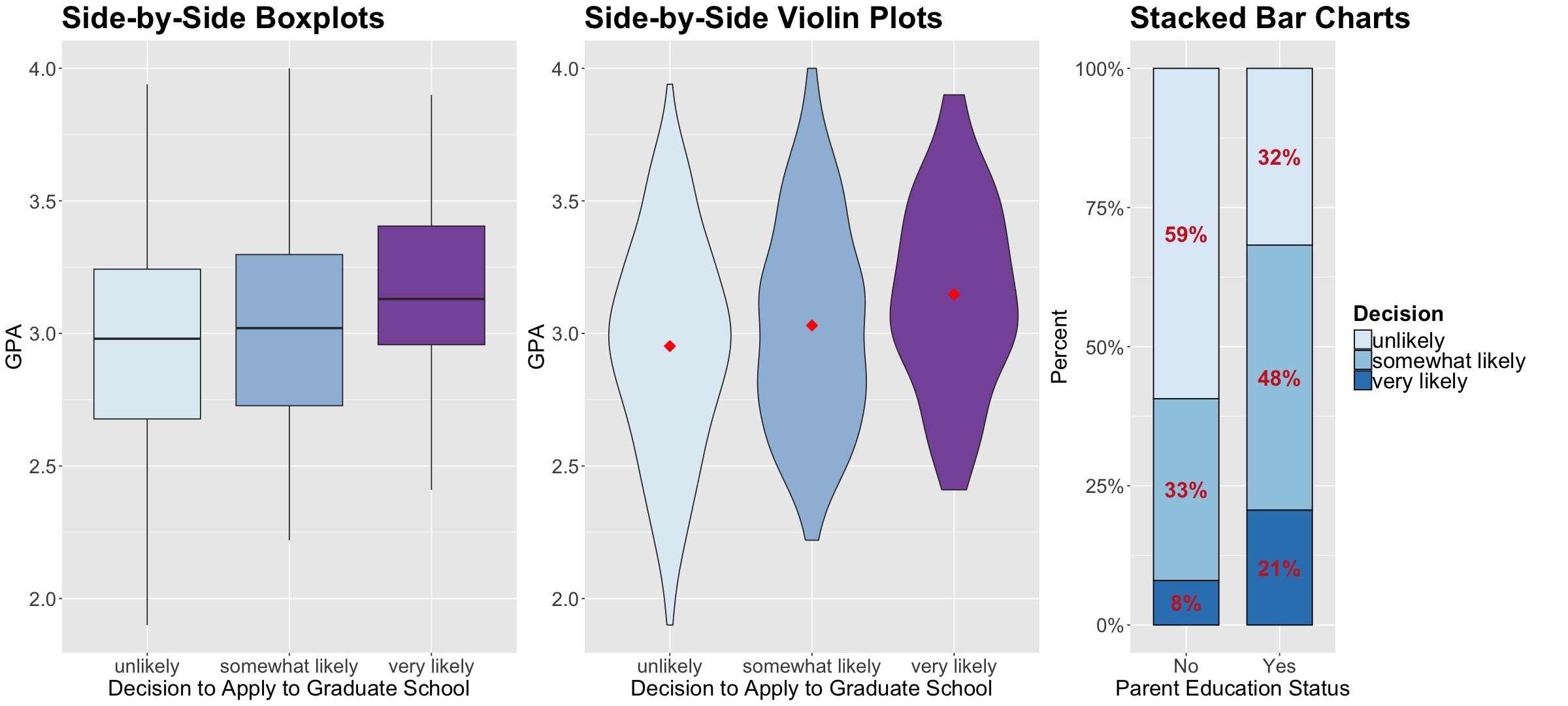
What can we see descriptively from the above plots?

4. Data Modelling Framework #

Let us suppose that a given discrete ordinal response \(Y_i\) (for \(i = 1, \dots, n\) ) has categories \(1, 2, \dots, m\) in a training set of size \(n\) .

Categories \(1, 2, \dots, m\) implicate an ordinal scale here , i.e., \(1 < 2 < \dots < m\) .

Also, note there is more than one class of Ordinal Logistic regression. We will review the proportional odds model (a cumulative logit model ).

We set up the Ordinal Logistical regression model for this specific dataset with \(m = 3\) . For the \(i\) th observation with the continuous \(X_{i, \texttt{GPA}}\) and the dummy variable

the model will indicate how each one of the regressors affects the cumulative logarithm of the odds in decision for the following \(2\) situations:

Then, we have the following system of \(2\) equations:

The system has \(2\) intercepts but only \(2\) regression coefficients . Check the signs of the common \(\beta_1\) and \(\beta_2\) , which are minuses. This is a fundamental parameterization of the proportional odds model.

To make coefficient intepretation easier, we could re-expresss the equations of \(\eta_i^{(\texttt{somewhat likely})}\) and \(\eta_i^{(\texttt{unlikely})}\) as follows:

Both regression coefficients ( \(\beta_1\) and \(\beta_2\) ) have a multiplicative effect on the odds on the left-hand side. Moreover, given the proportional odds assumptions , the regressor effects are the same for both cumulative odds.

What is the math for the general case with \(m\) response categories and \(k\) regressors?

Before going into the model’s mathematical notation, we have to point out that Ordinal Logistic regression will indicate how each one of the \(k\) regressors \(X_{i,1}, \dots, X_{i,k}\) affects the cumulative logarithm of the odds in the ordinal response for the following \(m - 1\) situations:

These \(m - 1\) situations are translated into cumulative probabilities using the logarithms of the odds on the left-hand side ( \(m - 1\) link functions) subject to the linear combination of the \(k\) regressors \(X_{i,j}\) (for \(j = 1, \dots, k\) ):

Note that the system above has \(m - 1\) intercepts but only \(k\) regression coefficients . In general, the previous \(m - 1\) equations can be generalized for levels \(j = m - 1, \dots, 1\) as follows:

The probability that \(Y_i\) will fall in the category \(j\) can be computed as follows:

which leads to

You will prove why we have proportional odds in this model in the challenging Exercise 4 of lab2 .

Let us check the next in-class question via iClicker .

Exercise 10

Suppose we have a case with an ordered response of five levels and four continuous regressors; how many link functions, intercepts, and coefficients will our Ordinal Logistic regression model have under a proportional odds assumption?

A. Four link functions, four intercepts, and sixteen regression coefficients.

B. Five link functions, five intercepts, and five regression coefficients.

C. Five link functions, five intercepts, and twenty regression coefficients.

D. Four link functions, four intercepts, and four regression coefficients.

A Graphical Intuition of the Proportional Odds Assumption #

The challenging Exercise 4 in lab2 is about showing mathematically what the proportional odds assumption stands for in the Ordinal Logistic regression model with \(k\) regressors and a training set size of \(n\) , using a response of \(m\) levels in general. That said, let us show the graphical intuition with an example of an ordinal response of \(5\) levels and a single continuous regressor \(X_{i , 1}\) ( which is unbounded! ).

The system of cumulative logit equations is the following:

This above system could be mathematically expressed as follows:

Note we have four intercepts \((\beta_0^{(1)}, \beta_0^{(2)}, \beta_0^{(3)}, \beta_0^{(4)})\) and a single coefficient \(\beta_1\) . Moreover, assume we estimate these five parameters to be the following:

Let us check our estimated sigmoid functions! As we can see in Fig. 9 , the proportional odds assumption also implicates proportional sigmoid functions.

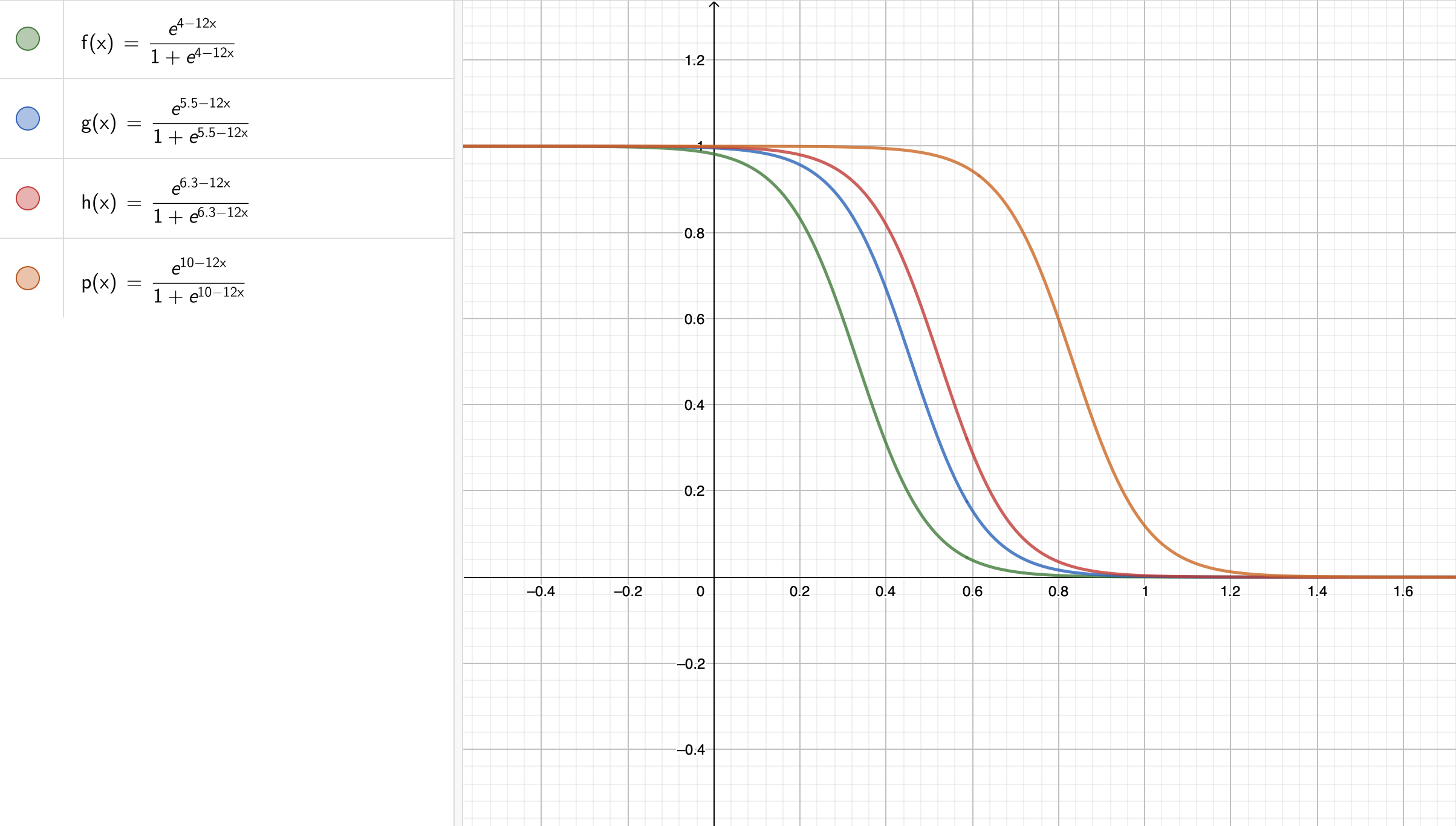
Fig. 9 Sigmoid functions under a proportional odds assumption (Copyright GeoGebra® , 2024). #

5. Estimation #

All parameters in the Ordinal Logistic regression model are also unknown. Therefore, model estimates are obtained through maximum likelihood , where we also assume a Multinomial joint probability mass function of the \(n\) responses \(Y_i\) .

To fit the model with the package MASS , we use the function polr() , which obtains the corresponding estimates. The argument Hess = TRUE is required to compute the Hessian matrix of the log-likelihood function , which is used to obtain the standard errors of the estimates.

Maximum likelihood estimation in this regression model is quite complex compared to the challenging Exercise 5 in lab1 for Binary Logistic regression. Thus, the proof will be out of the scope of this course.

6. Inference #

We can determine whether a regressor is statistically associated with the logarithm of the cumulative odds through hypothesis testing for the parameters \(\beta_j\) . We also use the Wald statistic \(z_j:\)

to test the hypotheses

The null hypothesis \(H_0\) indicates that the \(j\) th regressor associated to \(\beta_j\) does not affect the response variable in the model, and the alternative hypothesis \(H_a\) otherwise. Moreover, provided the sample size \(n\) is large enough, \(z_j\) has an approximately Standard Normal distribution under \(H_0\) .

R provides the corresponding \(p\) -values for each \(\beta_j\) . The smaller the \(p\) -value, the stronger the evidence against the null hypothesis \(H_0\) . As in the previous regression models, we would set a predetermined significance level \(\alpha\) (usually taken to be 0.05) to infer if the \(p\) -value is small enough. If the \(p\) -value is smaller than the predetermined level \(\alpha\) , then you could claim that there is evidence to reject the null hypothesis. Hence, \(p\) -values that are small enough indicate that the data provides evidence in favour of association ( or causation in the case of an experimental study! ) between the response variable and the \(j\) th regressor.

Furthermore, given a specified level of confidence where \(\alpha\) is the significance level, we can construct approximate \((1 - \alpha) \times 100\%\) confidence intervals for the corresponding true value of \(\beta_j\) :

where \(z_{\alpha/2}\) is the upper \(\alpha/2\) quantile of the Standard Normal distribution .

Function polr() does not provide \(p\) -values, but we can compute them as follows:

Terms unlikely|somewhat likely and somewhat likely|very likely refer to the estimated intercepts \(\hat{\beta}_0^{(\texttt{unlikely})}\) and \(\hat{\beta}_0^{(\texttt{somewhat likely})}\) , respectively ( note the hat notation ).

Finally, we see that those coefficients associated with GPA and parent_ed are statistically significant with \(\alpha = 0.05\) .

Function confint() can provide the 95% confidence intervals for the estimates contained in tidy() .

7. Coefficient Interpretation #

The interpretation of the Ordinal Logistic regression coefficients will change since we are modelling cumulative probabilities. Let us interpret the association of decision with GPA and parent_ed .

By using the column exp.estimate , along with the model equations on the original scale of the cumulative odds , we interpret the two regression coefficients above by each odds as follows:

For the odds

\(\beta_1\) : “for each one-unit increase in the GPA , the odds that the student is very likely versus somewhat likely or unlikely to apply to graduate school increase by \(\exp \left( \hat{\beta}_1 \right) = 1.82\) times (while holding parent_ed constant).”

\(\beta_2\) : “for those respondents whose parents attended to graduate school, the odds that the student is very likely versus somewhat likely or unlikely to apply to graduate school increase by \(\exp \left( \hat{\beta}_2 \right) = 2.86\) times (when compared to those respondents whose parents did not attend to graduate school and holding GPA constant).”

\(\beta_1\) : “for each one-unit increase in the GPA , the odds that the student is very likely or somewhat likely versus unlikely to apply to graduate school increase by \(\exp \left( \hat{\beta}_1 \right) = 1.82\) times (while holding parent_ed constant).”

\(\beta_2\) : “for those respondents whose parents attended to graduate school, the odds that the student is very likely or somewhat likely versus unlikely to apply to graduate school increase by \(\exp \left( \hat{\beta}_2 \right) = 2.86\) times (when compared to those respondents whose parents did not attend to graduate school and holding GPA constant).”

8. Predictions #

Aside from our main statistical inquiries , using the function predict() with the object ordinal_model , we can obtain the estimated probabilities to apply to graduate school (associated to unlikely , somewhat likely , and very likely ) for a student with a GPA of 3.5 whose parents attended to graduate school.

We can see that it is somewhat likely to apply to graduate school with a probability of 0.48. Thus, we could classify the student in this ordinal category.

Unfortunately, predict() with polr() does not provide a quick way to compute this model’s corresponding predicted cumulative odds for a new observation. Nonetheless, we could use function vglm() (from package VGAM ) again while keeping in mind that this function labels the response categories as numbers . Let us check this for decision with levels() .

Hence, unlikely is 1 , somewhat likely is 2 , and very likely is 3 . Now, let us use vglm() with propodds to fit the same model (named ordinal_model_vglm ) as follows:

We will double-check whether ordinal_model_vglm provides the same classification probabilities via predict() . Note that the function parameterization changes to type = "response" .

Yes, we get identical results using vglm() . Now, let us use predict() with ordinal_model_vglm to obtain the predicted cumulative odds for a student with a GPA of 3.5 whose parents attended to graduate school (via argument type = "link" in predict() ).

Then, let us take these predictions to the odds’ original scale via exp() .

Again, we see the numeric labels (a drawback of using vglm() ). We interpret these predictions as follows:

\(\frac{P(Y_i = \texttt{very likely} \mid X_{i, \texttt{GPA}},X_{i, \texttt{parent_ed}})}{P(Y_i \leq \texttt{somewhat likely} \mid X_{i, \texttt{GPA}},X_{i, \texttt{parent_ed}})}\) , i.e., P[Y>=3] (label 3 , very likely ): “ a student, with a GPA of 3.5 whose parents attended to graduate school, is 3.03 ( \(1 / 0.33\) ) times somewhat likely or unlikely versus very likely to apply to graduate school .” This prediction goes in line with the predicted probabilities above, given that somewhat likely has a probability of 0.48 and unlikely a probability of 0.27.

\(\frac{P(Y_i \geq \texttt{somewhat likely} \mid X_{i, \texttt{GPA}},X_{i, \texttt{parent_ed}})}{P(Y_i = \texttt{unlikely} \mid X_{i, \texttt{GPA}},X_{i, \texttt{parent_ed}})}\) , i.e., P[Y>=2] (label 2 , somewhat likely ): “ a student, with a GPA of 3.5 whose parents attended to graduate school, is 2.68 times very likely or somewhat likely versus unlikely to apply to graduate school .” This prediction goes in line with the predicted probabilities above, given that somewhat likely has a probability of 0.48 and very likely a probability of 0.25.

9. Model Selection #

To perform model selection , we can use the same techniques from the Binary Logistic regression model (check 8. Model Selection ). That said, some R coding functions might not be entirely available for the polr() models. Still, these statistical techniques and metrics can be manually coded.

10. Non-proportional Odds #

Now, we might wonder

What happens if we do not fulfil the proportional odds assumption in our Ordinal Logistic regression model?

10.1. The Brant-Wald Test #

It is essential to remember that the Ordinal Logistic model under the proportional odds assumption is the first step when performing Regression Analysis on an ordinal response.

Once this model has been fitted, it is possible to assess whether it fulfils this strong assumption statistically .

We can do it via the Brant-Wald test:

This tool performs statistically assesses whether our model globally fulfils this assumption. It has the following hypotheses:

Moreover, it also performs further hypothesis testing on each regressor. With \(k\) regressors for \(j = 1, \dots, k\) ; we have the following hypotheses:

Function brant() from package brant implements this tool, which can be used in our polr() object ordinal_model :

The row Omnibus represents the global model, while the other two rows correspond to our two regressors: parent_ed and GPA . Note that with \(\alpha = 0.05\) , we are completely fulfilling the proportional odds assumption (the column probability delivers the corresponding \(p\) -values).

The Brant Wald test essentially compares this basic Ordinal Logistic regression model of \(k-1\) cumulative logit functions versus a combination of k − 1 correlated binary logistic regressions.

10.2. A Non-proportional Odds Model #

Suppose that our example case does not fulfil the proportional odds assumption according to the Brant Wald test. It is possible to have a model under a non-proportional odds assumption as follows:

This is called a Generalized Ordinal Logistic regression model . This class of models can be fit via the function cumulative() from package VGAM . Note that estimation, inference, coefficient interpretation, and predictions are conducted in a similar way compared to the proportional odds model .

Exercise 11

Why would we have to be cautious when fitting a non-proportional odds model in the context of a response with a considerable number of ordinal levels and regressors?

11. Wrapping Up on Categorical Regression Models #

Multinomial and Ordinal Logistic regression models address cases where our response is discrete and categorical. These models are another class GLMs with their corresponding link functions.

Multinomial Logistic regression approaches nominal responses. It heavily relies on a baseline response level and the odds’ natural logarithm.

Ordinal Logistic regression approaches ordinal responses. It relies on cumulative odds on an ordinal scale.

We have to be careful with coefficient interpretations in these models, especially with the cumulative odds. This will imply an effective communication of these estimated models for inferential matters.

Handbook of Regression Modeling in People Analytics : With Examples in R, Python and Julia

7 proportional odds logistic regression for ordered category outcomes.

Often our outcomes will be categorical in nature, but they will also have an order to them. These are sometimes known as ordinal outcomes. Some very common examples of this include ratings of some form, such as job performance ratings or survey responses on Likert scales. The appropriate modeling approach for these outcome types is ordinal logistic regression. Surprisingly, this approach is frequently not understood or adopted by analysts. Often they treat the outcome as a continuous variable and perform simple linear regression, which can lead to wildly inaccurate inferences. Given the prevalence of ordinal outcomes in people analytics, it would serve analysts well to know how to run ordinal logistic regression models, how to interpret them and how to confirm their validity.

In fact, there are numerous known ways to approach the inferential modeling of ordinal outcomes, all of which build on the theory of linear, binomial and multinomial regression which we covered in previous chapters. In this chapter, we will focus on the most commonly adopted approach: proportional odds logistic regression. Proportional odds models (sometimes known as constrained cumulative logistic models) are more attractive than other approaches because of their ease of interpretation but cannot be used blindly without important checking of underlying assumptions.

7.1 When to use it

7.1.1 intuition for proportional odds logistic regression.

Ordinal outcomes can be considered to be suitable for an approach somewhere ‘between’ linear regression and multinomial regression. In common with linear regression, we can consider our outcome to increase or decrease dependent on our inputs. However, unlike linear regression the increase and decrease is ‘stepwise’ rather than continuous, and we do not know that the difference between the steps is the same across the scale. In medical settings, the difference between moving from a healthy to an early-stage disease may not be equivalent to moving from an early-stage disease to an intermediate- or advanced-stage. Equally, it may be a much bigger psychological step for an individual to say that they are very dissatisfied in their work than it is to say that they are very satisfied in their work. In this sense, we are analyzing categorical outcomes similar to a multinomial approach.

To formalize this intuition, we can imagine a latent version of our outcome variable that takes a continuous form, and where the categories are formed at specific cutoff points on that continuous variable. For example, if our outcome variable \(y\) represents survey responses on an ordinal Likert scale of 1 to 5, we can imagine we are actually dealing with a continuous variable \(y'\) along with four increasing ‘cutoff points’ for \(y'\) at \(\tau_1\) , \(\tau_2\) , \(\tau_3\) and \(\tau_4\) . We then define each ordinal category as follows: \(y = 1\) corresponds to \(y' \le \tau_1\) , \(y \le 2\) to \(y' \le \tau_2\) , \(y \le 3\) to \(y' \le \tau_3\) and \(y \le 4\) to \(y' \le \tau_4\) . Further, at each such cutoff \(\tau_k\) , we assume that the probability \(P(y > \tau_k)\) takes the form of a logistic function. Therefore, in the proportional odds model, we ‘divide’ the probability space at each level of the outcome variable and consider each as a binomial logistic regression model. For example, at rating 3, we generate a binomial logistic regression model of \(P(y > \tau_3)\) , as illustrated in Figure 7.1 .

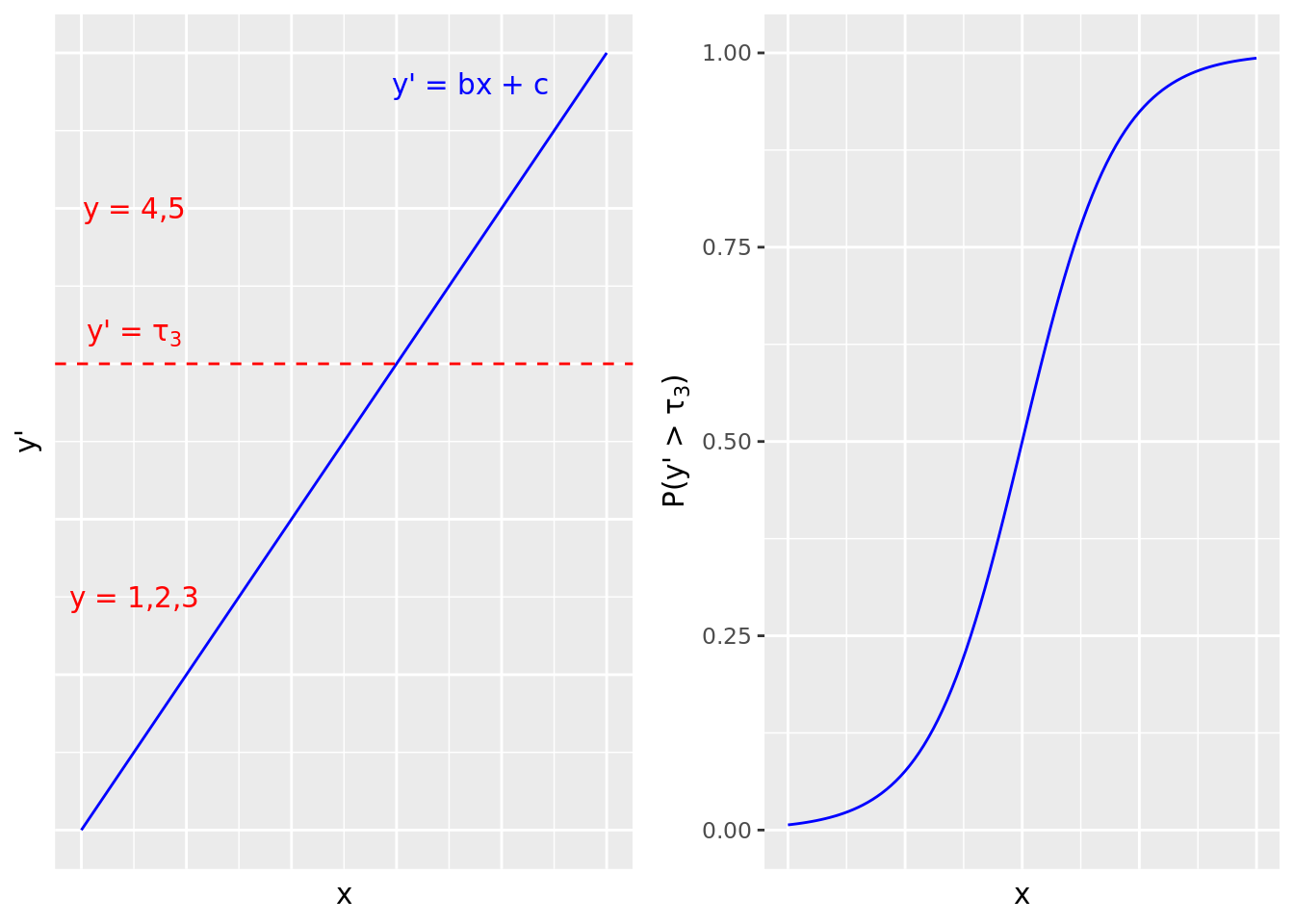
Figure 7.1: Proportional odds model illustration for a 5-point Likert survey scale outcome greater than 3 on a single input variable. Each cutoff point in the latent continuous outcome variable gives rise to a binomial logistic function.

This approach leads to a highly interpretable model that provides a single set of coefficients that are agnostic to the outcome category. For example, we can say that each unit increase in input variable \(x\) increases the odds of \(y\) being in a higher category by a certain ratio.

7.1.2 Use cases for proportional odds logistic regression

Proportional odds logistic regression can be used when there are more than two outcome categories that have an order. An important underlying assumption is that no input variable has a disproportionate effect on a specific level of the outcome variable. This is known as the proportional odds assumption. Referring to Figure 7.1 , this assumption means that the ‘slope’ of the logistic function is the same for all category cutoffs 34 . If this assumption is violated, we cannot reduce the coefficients of the model to a single set across all outcome categories, and this modeling approach fails. Therefore, testing the proportional odds assumption is an important validation step for anyone running this type of model.

Examples of problems that can utilize a proportional odds logistic regression approach include:

• Understanding the factors associated with higher ratings in an employee survey on a Likert scale
• Understanding the factors associated with higher job performance ratings on an ordinal performance scale
• Understanding the factors associated with voting preference in a ranked preference voting system (for example, proportional representation systems)

7.1.3 Walkthrough example

You are an analyst for a sports broadcaster who is doing a feature on player discipline in professional soccer games. To prepare for the feature, you have been asked to verify whether certain metrics are significant in influencing the extent to which a player will be disciplined by the referee for unfair or dangerous play in a game. You have been provided with data on over 2000 different players in different games, and the data contains these fields:

• discipline : A record of the maximum discipline taken by the referee against the player in the game. ‘None’ means no discipline was taken, ‘Yellow’ means the player was issued a yellow card (warned), ‘Red’ means the player was issued a red card and ordered off the field of play.
• n_yellow_25 is the total number of yellow cards issued to the player in the previous 25 games they played prior to this game.
• n_red_25 is the total number of red cards issued to the player in the previous 25 games they played prior to this game.
• position is the playing position of the player in the game: ‘D’ is defense (including goalkeeper), ‘M’ is midfield and ‘S’ is striker/attacker.
• level is the skill level of the competition in which the game took place, with 1 being higher and 2 being lower.
• country is the country in which the game took place—England or Germany.
• result is the result of the game for the team of the player—‘W’ is win, ‘L’ is lose, ‘D’ is a draw/tie.

Let’s download the soccer data set and take a quick look at it.

Let’s also take a look at the structure of the data.

We see that there are numerous fields that need to be converted to factors before we can model them. Firstly, our outcome of interest is discipline and this needs to be an ordered factor, which we can choose to increase with the seriousness of the disciplinary action.

We also know that position , country , result and level are categorical, so we convert them to factors. We could in fact choose to convert result and level into ordered factors if we so wish, but this is not necessary for input variables, and the results are usually a little bit easier to read as nominal factors.

Now our data is in a position to run a model. You may wish to conduct some exploratory data analysis at this stage similar to previous chapters, but from this chapter onward we will skip this and focus on the modeling methodology.

7.2 Modeling ordinal outcomes under the assumption of proportional odds

For simplicity, and noting that this is easily generalizable, let’s assume that we have an ordinal outcome variable \(y\) with three levels similar to our walkthrough example, and that we have one input variable \(x\) . Let’s call the outcome levels 1, 2 and 3. To follow our intuition from Section 7.1.1 , we can model a linear continuous variable \(y' = \alpha_1x + \alpha_0 + E\) , where \(E\) is some error with a mean of zero, and two increasing cutoff values \(\tau_1\) and \(\tau_2\) . We define \(y\) in terms of \(y'\) as follows: \(y = 1\) if \(y' \le \tau_1\) , \(y = 2\) if \(\tau_1 < y' \le \tau_2\) and \(y = 3\) if \(y' > \tau_2\) .

7.2.1 Using a latent continuous outcome variable to derive a proportional odds model

Recall from Section 4.5.3 that our linear regression approach assumes that our residuals \(E\) around our line \(y' = \alpha_1x + \alpha_0\) have a normal distribution. Let’s modify that assumption slightly and instead assume that our residuals take a logistic distribution based on the variance of \(y'\) . Therefore, \(y' = \alpha_1x + \alpha_0 + \sigma\epsilon\) , where \(\sigma\) is proportional to the variance of \(y'\) and \(\epsilon\) follows the shape of a logistic function. That is

\[ P(\epsilon \leq z) = \frac{1}{1 + e^{-z}} \]

Let’s look at the probability that our ordinal outcome variable \(y\) is in its lowest category.

\[ \begin{aligned} P(y = 1) &= P(y' \le \tau_1) \\ &= P(\alpha_1x + \alpha_0 + \sigma\epsilon \leq \tau_1) \\ &= P(\epsilon \leq \frac{\tau_1 - \alpha_1x - \alpha_0}{\sigma}) \\ &= P(\epsilon \le \gamma_1 - \beta{x}) \\ &= \frac{1}{1 + e^{-(\gamma_1 - \beta{x})}} \end{aligned} \]

where \(\gamma_1 = \frac{\tau_1 - \alpha_0}{\sigma}\) and \(\beta = \frac{\alpha_1}{\sigma}\) .

Since our only values for \(y\) are 1, 2 and 3, similar to our derivations in Section 5.2 , we conclude that \(P(y > 1) = 1 - P(y = 1)\) , which calculates to

\[ P(y > 1) = \frac{e^{-(\gamma_1 - \beta{x})}}{1 + e^{-(\gamma_1 - \beta{x})}} \] Therefore \[ \begin{aligned} \frac{P(y = 1)}{P(y > 1)} = \frac{\frac{1}{1 + e^{-(\gamma_1 - \beta{x})}}}{\frac{e^{-(\gamma_1 - \beta{x})}}{1 + e^{-(\gamma_1 - \beta{x})}}} = e^{\gamma_1 - \beta{x}} \end{aligned} \]

By applying the natural logarithm, we conclude that the log odds of \(y\) being in our bottom category is

\[ \mathrm{ln}\left(\frac{P(y = 1)}{P(y > 1)}\right) = \gamma_1 - \beta{x} \] In a similar way we can derive the log odds of our ordinal outcome being in our bottom two categories as

\[ \mathrm{ln}\left(\frac{P(y \leq 2)}{P(y = 3)}\right) = \gamma_2 - \beta{x} \] where \(\gamma_2 = \frac{\tau_2 - \alpha_0}{\sigma}\) . One can easily see how this generalizes to an arbitrary number of ordinal categories, where we can state the log odds of being in category \(k\) or lower as

\[ \mathrm{ln}\left(\frac{P(y \leq k)}{P(y > k)}\right) = \gamma_k - \beta{x} \] Alternatively, we can state the log odds of being in a category higher than \(k\) by simply inverting the above expression:

\[ \mathrm{ln}\left(\frac{P(y > k)}{P(y \leq k)}\right) = -(\gamma_k - \beta{x}) = \beta{x} - \gamma_k \]

By taking exponents we see that the impact of a unit change in \(x\) on the odds of \(y\) being in a higher ordinal category is \(\beta\) , irrespective of what category we are looking at . Therefore we have a single coefficient to explain the effect of \(x\) on \(y\) throughout the ordinal scale. Note that there are still different intercept coefficients \(\gamma_1\) and \(\gamma_2\) for each level of the ordinal scale.

7.2.2 Running a proportional odds logistic regression model

The MASS package provides a function polr() for running a proportional odds logistic regression model on a data set in a similar way to our previous models. The key (and obvious) requirement is that the outcome is an ordered factor. Since we did our conversions in Section 7.1.3 we are ready to run this model. We will start by running it on all input variables and let the polr() function handle our dummy variables automatically.

We can see that the summary returns a single set of coefficients on our input variables as we expect, with standard errors and t-statistics. We also see that there are separate intercepts for the various levels of our outcomes, as we also expect. In interpreting our model, we generally don’t have a great deal of interest in the intercepts, but we will focus on the coefficients. First we would like to obtain p-values, so we can add a p-value column using the conversion methods from the t-statistic which we learned in Section 3.3.1 35 .

Next we can convert our coefficients to odds ratios.

We can display all our critical statistics by combining them into a dataframe.

Taking into consideration the p-values, we can interpret our coefficients as follows, in each case assuming that other coefficients are held still:

• Each additional yellow card received in the prior 25 games is associated with an approximately 38% higher odds of greater disciplinary action by the referee.
• Each additional red card received in the prior 25 games is associated with an approximately 47% higher odds of greater disciplinary action by the referee.
• Strikers have approximately 50% lower odds of greater disciplinary action from referees compared to Defenders.
• A player on a team that lost the game has approximately 62% higher odds of greater disciplinary action versus a player on a team that drew the game.
• A player on a team that won the game has approximately 52% lower odds of greater disciplinary action versus a player on a team that drew the game.

We can, as per previous chapters, remove the level and country variables from this model to simplify it if we wish. An examination of the coefficients and the AIC of the simpler model will reveal no substantial difference, and therefore we proceed with this model.

7.2.3 Calculating the likelihood of an observation being in a specific ordinal category

Recall from Section 7.2.1 that our proportional odds model generates multiple stratified binomial models, each of which has following form:

\[ P(y \leq k) = P(y' \leq \tau_k) \] Note that for an ordinal variable \(y\) , if \(y \leq k\) and \(y > k-1\) , then \(y = k\) . Therefore \(P(y = k) = P(y \leq k) - P(y \leq k - 1)\) . This means we can calculate the specific probability of an observation being in each level of the ordinal variable in our fitted model by simply calculating the difference between the fitted values from each pair of adjacent stratified binomial models. In our walkthrough example, this means we can calculate the specific probability of no action from the referee, or a yellow card being awarded, or a red card being awarded. These can be viewed using the fitted() function.

It can be seen from this output how ordinal logistic regression models can be used in predictive analytics by classifying new observations into the ordinal category with the highest fitted probability. This also allows us to graphically understand the output of a proportional odds model. Interactive Figure 7.2 shows the output from a simpler proportional odds model fitted against the n_yellow_25 and n_red_25 input variables, with the fitted probabilities of each level of discipline from the referee plotted on the different colored surfaces. We can see in most situations that no discipline is the most likely outcome and a red card is the least likely outcome. Only at the upper ends of the scales do we see the likelihood of discipline overcoming the likelihood of no discipline, with a strong likelihood of red cards for those with an extremely poor recent disciplinary record.

Figure 7.2: 3D visualization of a simple proportional odds model for discipline fitted against n_yellow_25 and n_red_25 in the soccer data set. Blue represents the probability of no discipline from the referee. Yellow and red represent the probability of a yellow card and a red card, respectively.

7.2.4 Model diagnostics

Similar to binomial and multinomial models, pseudo- \(R^2\) methods are available for assessing model fit, and AIC can be used to assess model parsimony. Note that DescTools::PseudoR2() also offers AIC.

There are numerous tests of goodness-of-fit that can apply to ordinal logistic regression models, and this area is the subject of considerable recent research. The generalhoslem package in R contains routes to four possible tests, with two of them particularly recommended for ordinal models. Each work in a similar way to the Hosmer-Lemeshow test discussed in Section 5.3.2 , by dividing the sample into groups and comparing the observed versus the fitted outcomes using a chi-square test. Since the null hypothesis is a good model fit, low p-values indicate potential problems with the model. We run these tests below for reference. For more information, see Fagerland and Hosmer ( 2017 ) , and for a really intensive treatment of ordinal data modeling Agresti ( 2010 ) is recommended.

7.3 Testing the proportional odds assumption

As we discussed earlier, the suitability of a proportional odds logistic regression model depends on the assumption that each input variable has a similar effect on the different levels of the ordinal outcome variable. It is very important to check that this assumption is not violated before proceeding to declare the results of a proportional odds model valid. There are two common approaches to validating the proportional odds assumption, and we will go through each of them here.

7.3.1 Sighting the coefficients of stratified binomial models

As we learned above, proportional odds regression models effectively act as a series of stratified binomial models under the assumption that the ‘slope’ of the logistic function of each stratified model is the same. We can verify this by actually running stratified binomial models on our data and checking for similar coefficients on our input variables. Let’s use our walkthrough example to illustrate.

Let’s create two columns with binary values to correspond to the two higher levels of our ordinal variable.

Now let’s create two binomial logistic regression models for the two higher levels of our outcome variable.

We can now display the coefficients of both models and examine the difference between them.

Ignoring the intercept, which is not of concern here, the differences appear relatively small. Large differences in coefficients would indicate that the proportional odds assumption is likely violated and alternative approaches to the problem should be considered.

7.3.2 The Brant-Wald test

In the previous method, some judgment is required to decide whether the coefficients of the stratified binomial models are ‘different enough’ to decide on violation of the proportional odds assumption. For those requiring more formal support, an option is the Brant-Wald test. Under this test, a generalized ordinal logistic regression model is approximated and compared to the calculated proportional odds model. A generalized ordinal logistic regression model is simply a relaxing of the proportional odds model to allow for different coefficients at each level of the ordinal outcome variable.

The Wald test is conducted on the comparison of the proportional odds and generalized models. A Wald test is a hypothesis test of the significance of the difference in model coefficients, producing a chi-square statistic. A low p-value in a Brant-Wald test is an indicator that the coefficient does not satisfy the proportional odds assumption. The brant package in R provides an implementation of the Brant-Wald test, and in this case supports our judgment that the proportional odds assumption holds.

A p-value of less than 0.05 on this test—particularly on the Omnibus plus at least one of the variables—should be interpreted as a failure of the proportional odds assumption.

7.3.3 Alternatives to proportional odds models

The proportional odds model is by far the most utilized approach to modeling ordinal outcomes (not least because of neglect in the testing of the underlying assumptions). But as we have learned, it is not always an appropriate model choice for ordinal outcomes. When the test of proportional odds fails, we need to consider a strategy for remodeling the data. If only one or two variables fail the test of proportional odds, a simple option is to remove those variables. Whether or not we are comfortable doing this will depend very much on the impact on overall model fit.

In the event where the option to remove variables is unattractive, alternative models for ordinal outcomes should be considered. The most common alternatives (which we will not cover in depth here, but are explored in Agresti ( 2010 ) ) are:

• Baseline logistic model. This model is the same as the multinomial regression model covered in the previous chapter, using the lowest ordinal value as the reference.
• Adjacent-category logistic model. This model compares each level of the ordinal variable to the next highest level, and it is a constrained version of the baseline logistic model. The brglm2 package in R offers a function bracl() for calculating an adjacent category logistic model.
• Continuation-ratio logistic model. This model compares each level of the ordinal variable to all lower levels. This can be modeled using binary logistic regression techniques, but new variables need to be constructed from the data set to allow this. The R package rms has a function cr.setup() which is a utility for preparing an outcome variable for a continuation ratio model.

7.4 Learning exercises

7.4.1 discussion questions.

• Describe what is meant by an ordinal variable.
• Describe how an ordinal variable can be represented using a latent continuous variable.
• Describe the series of binomial logistic regression models that are components of a proportional odds regression model. What can you say about their coefficients?
• If \(y\) is an ordinal outcome variable with at least three levels, and if \(x\) is an input variable that has coefficient \(\beta\) in a proportional odds logistic regression model, describe how to interpret the odds ratio \(e^{\beta}\) .
• Describe some approaches for assessing the fit and goodness-of-fit of an ordinal logistic regression model.
• Describe how you would use stratified binomial logistic regression models to validate the key assumption for a proportional odds model.
• Describe a statistical significance test that can support or reject the hypothesis that the proportional odds assumption holds.
• Describe some possible options for situations where the proportional odds assumption is violated.

7.4.2 Data exercises

Load the managers data set via the peopleanalyticsdata package or download it from the internet 36 . It is a set of information of 571 managers in a sales organization and consists of the following fields:

• employee_id for each manager
• performance_group of each manager in a recent performance review: Bottom performer, Middle performer, Top performer
• yrs_employed : total length of time employed in years
• manager_hire : whether or not the individual was hired directly to be a manager (Y) or promoted to manager (N)
• test_score : score on a test given to all managers
• group_size : the number of employees in the group they are responsible for
• concern_flag : whether or not the individual has been the subject of a complaint by a member of their group
• mobile_flag : whether or not the individual works mobile (Y) or in the office (N)
• customers : the number of customer accounts the manager is responsible for
• high_hours_flag : whether or not the manager has entered unusually high hours into their timesheet in the past year
• transfers : the number of transfer requests coming from the manager’s group while they have been a manager
• reduced_schedule : whether the manager works part time (Y) or full time (N)
• city : the current office of the manager.

Construct a model to determine how the data provided may help explain the performance_group of a manager by following these steps:

• Convert the outcome variable to an ordered factor of increasing performance.
• Convert input variables to categorical factors as appropriate.
• Perform any exploratory data analysis that you wish to do.
• Run a proportional odds logistic regression model against all relevant input variables.
• Construct p-values for the coefficients and consider how to simplify the model to remove variables that do not impact the outcome.
• Calculate the odds ratios for your simplified model and write an interpretation of them.
• Estimate the fit of the simplified model using a variety of metrics and perform tests to determine if the model is a good fit for the data.
• Construct new outcome variables and use a stratified binomial approach to determine if the proportional odds assumption holds for your simplified model. Are there any input variables for which you may be concerned that the assumption is violated? What would you consider doing in this case?
• Use the Brant-Wald test to support or reject the hypothesis that the proportional odds assumption holds for your simplified model.
• Write a full report on your model intended for an audience of people with limited knowledge of statistics.

• Skip to primary navigation
• Skip to main content
• Skip to primary sidebar

Statistical Methods and Data Analytics

Ordinal Logistic Regression | SPSS Data Analysis Examples

Version info: Code for this page was tested in IBM SPSS 20.

Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics and potential follow-up analyses.

Examples of ordered logistic regression

Example 1: A marketing research firm wants to investigate what factors influence the size of soda (small, medium, large or extra large) that people order at a fast-food chain. These factors may include what type of sandwich is ordered (burger or chicken), whether or not fries are also ordered, and age of the consumer. While the outcome variable, size of soda, is obviously ordered, the difference between the various sizes is not consistent. The difference between small and medium is 10 ounces, between medium and large 8, and between large and extra large 12.

Example 2: A researcher is interested in what factors influence medaling in Olympic swimming.  Relevant predictors include at training hours, diet, age, and popularity of swimming in the athlete’s home country. The researcher believes that the distance between gold and silver is larger than the distance between silver and bronze.

Example 3: A study looks at factors that influence the decision of whether to apply to graduate school.  College juniors are asked if they are unlikely, somewhat likely, or very likely to apply to graduate school. Hence, our outcome variable has three categories. Data on parental educational status, whether the undergraduate institution is public or private, and current GPA is also collected. The researchers have reason to believe that the “distances” between these three points are not equal.  For example, the “distance” between “unlikely” and “somewhat likely” may be shorter than the distance between “somewhat likely” and “very likely”.

Description of the data

For our data analysis below, we are going to expand on Example 3 about applying to graduate school. We have simulated some data for this example and it can be obtained from here: ologit.sav This hypothetical data set has a three-level variable called apply (coded 0, 1, 2), that we will use as our outcome variable. We also have three variables that we will use as predictors: pared , which is a 0/1 variable indicating whether at least one parent has a graduate degree; public , which is a 0/1 variable where 1 indicates that the undergraduate institution is public and 0 private, and gpa , which is the student’s grade point average.

Let’s start with the descriptive statistics of these variables.

get file "D:\data\ologit.sav". freq var = apply pared public. descriptives var = gpa.

Analysis methods you might consider

Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable while others have either fallen out of favor or have limitations.

• Ordered logistic regression: the focus of this page.
• OLS regression: This analysis is problematic because the assumptions of OLS are violated when it is used with a non-interval outcome variable.
• ANOVA: If you use only one continuous predictor, you could “flip” the model around so that, say, gpa was the outcome variable and apply was the predictor variable. Then you could run a one-way ANOVA. This isn’t a bad thing to do if you only have one predictor variable (from the logistic model), and it is continuous.
• Multinomial logistic regression:  This is similar to doing ordered logistic regression, except that it is assumed that there is no order to the categories of the outcome variable (i.e., the categories are nominal). The downside of this approach is that the information contained in the ordering is lost.
• Ordered probit regression: This is very, very similar to running an ordered logistic regression. The main difference is in the interpretation of the coefficients.

Ordered logistic regression

Before we run our ordinal logistic model, we will see if any cells are empty or extremely small.  If any are, we may have difficulty running our model. There are two ways in SPSS that we can do this.  The first way is to make simple crosstabs.  The second way is to use the cellinfo option on the /print subcommand.  You should use the cellinfo option only with categorical predictor variables; the table will be long and difficult to interpret if you include continuous predictors.

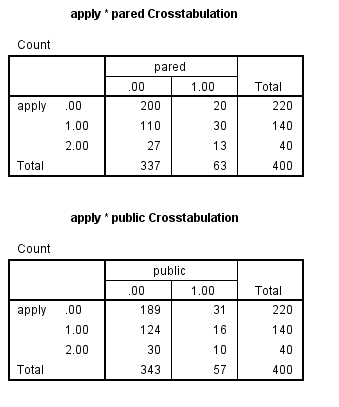
None of the cells is too small or empty (has no cases), so we will run our model. In the syntax below, we have included the link = logit subcommand, even though it is the default, just to remind ourselves that we are using the logit link function. Also note that if you do not include the print subcommand, only the Case Processing Summary table is provided in the output.

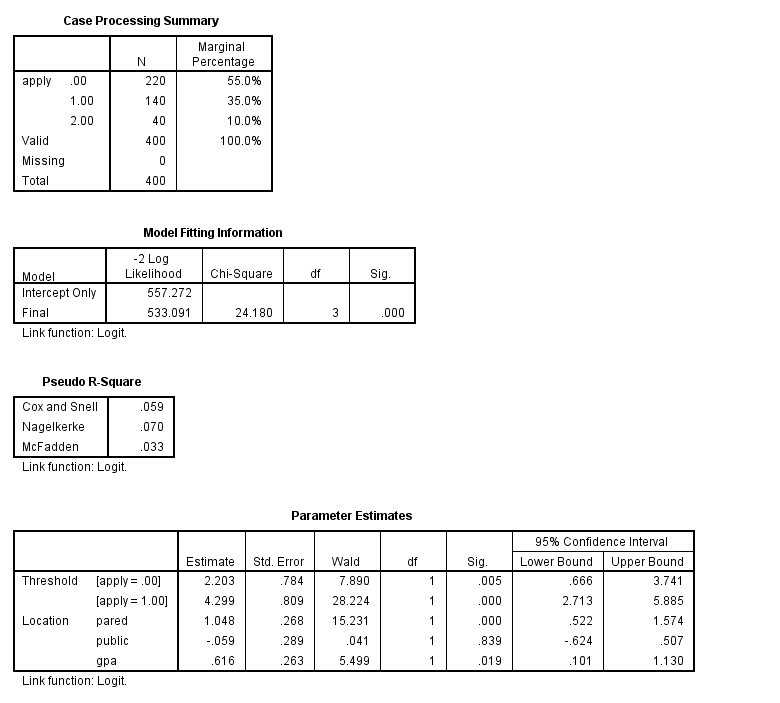
In the Case Processing Summary table, we see the number and percentage of cases in each level of our response variable. These numbers look fine, but we would be concerned if one level had very few cases in it. We also see that all 400 observations in our data set were used in the analysis. Fewer observations would have been used if any of our variables had missing values. By default, SPSS does a listwise deletion of cases with missing values.  Next we see the Model Fitting Information table, which gives the -2 log likelihood for the intercept-only and final models. The -2 log likelihood can be used in comparisons of nested models, but we won’t show an example of that here.

In the Parameter Estimates table we see the coefficients, their standard errors, the Wald test and associated p-values (Sig.), and the 95% confidence interval of the coefficients. Both pared and gpa are statistically significant; public is not.& So for pared , we would say that for a one unit increase in pared (i.e., going from 0 to 1), we expect a 1.05 increase in the ordered log odds of being in a higher level of apply , given all of the other variables in the model are held constant. For gpa , we would say that for a one unit increase in gpa , we would expect a 0.62 increase in the log odds of being in a higher level of apply , given that all of the other variables in the model are held constant. The thresholds are shown at the top of the parameter estimates output, and they indicate where the latent variable is cut to make the three groups that we observe in our data. Note that this latent variable is continuous. In general, these are not used in the interpretation of the results. Some statistical packages call the thresholds “cutpoints” (thresholds and cutpoints are the same thing); other packages, such as SAS report intercepts, which are the negative of the thresholds. In this example, the intercepts would be -2.203 and -4.299. For further information, please see the Stata FAQ: How can I convert Stata’s parameterization of ordered probit and logistic models to one in which a constant is estimated?

As of version 15 of SPSS, you cannot directly obtain the proportional odds ratios from SPSS. You can either use the SPSS Output Management System (OMS) to capture the parameter estimates and exponentiate them, or you can calculate them by hand. Please see Ordinal Regression by Marija J. Norusis for examples of how to do this. The commands for using OMS and calculating the proportional odds ratios is shown below. For more information on how to use OMS, please see our SPSS FAQ: How can I output my results to a data file in SPSS? Please note that the single quotes in the square brackets are important, and you will get an error message if they are omitted or unbalanced.

oms select tables /destination format = sav outfile = "D:\ologit_results.sav" /if commands = ['plum'] subtypes = ['Parameter Estimates']. plum apply with pared public gpa /link = logit /print = parameter. omsend. get file "D:\ologit_results.sav". rename variables Var2 = Predictor_Variables. * the next command deletes the thresholds from the data set. select if Var1 = "Location". exe. * the command below removes unnessary variables from the data set. * transformations cannot be pending for the command below to work, so * the exe. * above is necessary. delete variables Command_ Subtype_ Label_ Var1. compute expb = exp(Estimate). compute Lower_95_CI = exp(LowerBound). compute Upper_95_CI = exp(UpperBound). execute.

In the column expb we see the results presented as proportional odds ratios (the coefficient exponentiated). We have also calculated the lower and upper 95% confidence interval. We would interpret these pretty much as we would odds ratios from a binary logistic regression. For pared , we would say that for a one unit increase in pared, i.e., going from 0 to 1, the odds of high apply versus the combined middle and low categories are 2.85 greater, given that all of the other variables in the model are held constant. Likewise, the odds of the combined middle and high categories versus low apply is 2.85 times greater, given that all of the other variables in the model are held constant. For a one unit increase in gpa , the odds of the low and middle categories of apply versus the high category of apply are 1.85 times greater, given that the other variables in the model are held constant. Because of the proportional odds assumption (see below for more explanation), the same increase, 1.85 times, is found between low apply and the combined categories of middle and high apply .

One of the assumptions underlying ordered logistic (and ordered probit) regression is that the relationship between each pair of outcome groups is the same. In other words, ordered logistic regression assumes that the coefficients that describe the relationship between, say, the lowest versus all higher categories of the response variable are the same as those that describe the relationship between the next lowest category and all higher categories, etc. This is called the proportional odds assumption or the parallel regression assumption. Because the relationship between all pairs of groups is the same, there is only one set of coefficients (only one model). If this was not the case, we would need different models to describe the relationship between each pair of outcome groups. We need to test the proportional odds assumption, and we can use the tparallel option on the print subcommand. The null hypothesis of this chi-square test is that there is no difference in the coefficients between models, so we hope to get a non-significant result.

plum apply with pared public gpa /link = logit /print = tparallel.

The above test indicates that we have not violated the proportional odds assumption. If the proportional odds assumption was violated, we may want to go with multinomial logistic regression.

We we use these formulae to calculate the predicted probabilities for each level of the outcome, apply . Predicted probabilities are usually easier to understand than the coefficients or the odds ratios.

$$P(Y = 2) = \left(\frac{1}{1 + e^{-(a_{2}+b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3})}}\right)$$ $$P(Y = 1) = \left(\frac{1}{1 + e^{-(a_{1}+b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3})}}\right) – P(Y = 2)$$ $$P(Y = 0) = 1 – P(Y = 1) – P(Y = 2)$$

We will calculate the predicted probabilities using SPSS’ Matrix language. We will use pared as an example with a categorical predictor. Here we will see how the probabilities of membership to each category of apply change as we vary pared and hold the other variable at their means. As you can see, the predicted probability of being in the lowest category of apply is 0.59 if neither parent has a graduate level education and 0.34 otherwise. For the middle category of apply , the predicted probabilities are 0.33 and 0.47, and for the highest category of apply , 0.078 and 0.196 (annotations were added to the output for clarity). Hence, if neither of a respondent’s parents have a graduate level education, the predicted probability of applying to graduate school decreases. Note that the intercepts are the negatives of the thresholds. For a more detailed explanation of how to interpret the predicted probabilities and its relation to the odds ratio, please refer to FAQ: How do I interpret the coefficients in an ordinal logistic regression?

Matrix. * intercept1 intercept2 pared public gpa. * these coefficients are taken from the output. compute b = {-2.203 ; -4.299 ; 1.048 ; -.059 ; .616}. * overall design matrix including means of public and gpa. compute x = {{0, 1, 0; 0, 1, 1}, make(2, 1, .1425), make(2, 1, 2.998925)}. compute p3 = 1/(1 + exp(-x * b)). * overall design matrix including means of public and gpa. compute x = {{1, 0, 0; 1, 0, 1}, make(2, 1, .1425), make(2, 1, 2.998925)}. compute p2 = (1/(1 + exp(-x * b))) - p3. compute p1 = make(NROW(p2), 1, 1) - p2 - p3. compute p = {p1, p2, p3}. print p / FORMAT = F5.4 / title = "Predicted Probabilities for Outcomes 0 1 2 for pared 0 1 at means". End Matrix. Run MATRIX procedure: Predicted Probabilities for Outcomes 0 1 2 for pared 0 1 at means (apply=0) (apply=1) (apply=2) (pared=0) .5900 .3313 .0787 (pared=1) .3354 .4687 .1959 ------ END MATRIX -----

Below, we see the predicted probabilities for gpa at 2, 3 and 4. You can see that the predicted probability increases for both the middle and highest categories of apply as gpa increases (annotations were added to the output for clarity). For a more detailed explanation of how to interpret the predicted probabilities and its relation to the odds ratio, please refer to FAQ: How do I interpret the coefficients in an ordinal logistic regression?

Things to consider

• Perfect prediction: Perfect prediction means that one value of a predictor variable is associated with only one value of the response variable. If this happens, Stata will usually issue a note at the top of the output and will drop the cases so that the model can run.
• Sample size: Both ordered logistic and ordered probit, using maximum likelihood estimates, require sufficient sample size.  How big is big is a topic of some debate, but they almost always require more cases than OLS regression.
• Empty cells or small cells: You should check for empty or small cells by doing a crosstab between categorical predictors and the outcome variable. If a cell has very few cases, the model may become unstable or it might not run at all.
• Pseudo-R-squared:  There is no exact analog of the R-squared found in OLS.  There are many versions of pseudo-R-squares.  Please see Long and Freese 2005 for more details and explanations of various pseudo-R-squares.
• Diagnostics:  Doing diagnostics for non-linear models is difficult, and ordered logit/probit models are even more difficult than binary models.
• Agresti, A. (1996) An Introduction to Categorical Data Analysis . New York: John Wiley & Sons, Inc
• Agresti, A. (2002) Categorical Data Analysis, Second Edition . Hoboken, New Jersey: John Wiley & Sons, Inc.
• Liao, T. F. (1994) Interpreting Probability Models:  Logit, Probit, and Other Generalized Linear Models . Thousand Oaks, CA: Sage Publications, Inc.
• Powers, D. and Xie, Yu. Statistical Methods for Categorical Data Analysis.  Bingley, UK: Emerald Group Publishing Limited.

Your Name (required)

Your Email (must be a valid email for us to receive the report!)

Comment/Error Report (required)

How to cite this page

• © 2024 UC REGENTS

Ordinal Logistic Regression

• First Online: 01 January 2010

Cite this chapter

• David G. Kleinbaum 3 &
• Mitchel Klein 3  

Part of the book series: Statistics for Biology and Health ((SBH))

25k Accesses

23 Citations

In this chapter, the standard logistic model is extended to handle outcome variables that have more than two ordered categories. When the categories of the outcome variable have a natural order, ordinal logistic regression may be appropriate.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Author information

Authors and affiliations.

Department of Epidemiology, Emory University Rollins School of Public Health, Atlanta, GA, 30322, USA

David G. Kleinbaum & Mitchel Klein

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to David G. Kleinbaum .

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer Science+Business Media, LLC

About this chapter

Kleinbaum, D.G., Klein, M. (2010). Ordinal Logistic Regression. In: Logistic Regression. Statistics for Biology and Health. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-1742-3_13

Download citation

DOI : https://doi.org/10.1007/978-1-4419-1742-3_13

Published : 24 March 2010

Publisher Name : Springer, New York, NY

Print ISBN : 978-1-4419-1741-6

Online ISBN : 978-1-4419-1742-3

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research